Определение места изменения сечения

Предельный изгибающий момент для измененного сечения в месте стыкового шва пояса

       Расчетное сопротивление сварного шва сжатию, растяжению и изгибу по пределу текучести для полуавтоматической сварки и физических методов контроля качества шва R_wy = R_y = 2350 кг/см² (по таблице 3 СНиП II – 23 – 81*).

[M] = R_wy * W_x' = 2350*9240 = 217*10⁵ кг*см = 217 т*м

По эпюре изгибающих моментов (пункт 5.1) определяем, что сечения с изгибающим моментом М = 235 т*м находятся во II и V отсеках.

Положение сечений с М = 235 кг*м относительно опор А и В

М_I = ( R_A – 0,5 * P ) * X_лев - P *( X_лев – a) = [M] →

 → X_лев = ( [M] – Ра )/ 1,5 * P = (217- 38,8*1,9)/ (1,5*38,8) = 2,46м

Так как нагрузка симметричная, то X_лев = X_пр = 2,46 м.

Сечения отстоят от ближайших ребер на

|2,46 – 1,90|= 0,56 м = 56 см > 10 * t_w = 10*1 = 10 см → прочность обеспечена.

 

Проверки принятых сечений

5.8.1. По I группе предельных состояний

а) Проверка прочности основного сечения по нормальным напряжениям в месте действия максимального момента

σ = M_max / ( W_x * γ_c ) = 332*10⁵/(14430*1,0) = 2320 кг/см² < R_y = 2350 кг/см² → прочность обеспечена

б) Проверка прочности измененного сечения по касательным напряжениям на опоре

τ = 1,5 * Q_max / ( t_w * h_w ) = 1,5*97*10³ / (1,0*130) = 1119 кг/см² < R_s = 1360 кг/см² → прочность обеспечена.

в) Проверка прочности измененного сечения по приведенным напряжениям в месте изменения сечения  

σ = M * 0,5 * h_w / I_x' = 217*10⁵* 0,5*130 / (619*10³) = 2280 кг/см²

τ = Q_{x = х лев} / ( t_w * h_w ) = 58,2*10³ / (1*130) = 432 кг/см²

σ_пр = √ σ² + 3 *τ² = √ 2280²+432² = 2350 кг/см² < 1,15 * R_y * γ_c = 1,15*2350*1,0 = 2700 кг/см² →       → прочность обеспечена

г) Проверка общей устойчивости балки

Согласно пункту 5.16 СНиП II – 23 – 81* : l_ef = a = 190 см;

b = b_f' = 25 см;

t = t _f' = 2 см;

h = 2* z = 2*66 = 132 см.

Расчетное сопротивление материала R_y =  2350 кг/см².

l_ef / b ≤ ( 0,41 + 0,0032*b / t + ( 0,73 – 0,016 * b / t ) * b / h ) * √ Е / R_y

190/25 = 7,6 < (0,41+0,0032*25/2+(0,73-0,016*25/2)*25/132)*√2,1*10⁶/2350 = 16,4 → общая устойчивость обеспечена

5.8.2. По II группе предельных состояний по деформативности при нормальных условиях эксплуатации

Коэффициент, учитывающий уменьшение жесткости балки вследствие перемены сечения, 0,9.

f / L = 0,1 *M^н_max * L / ( 0,9 * E * I_x ) = 0,1 *M_max * L / ( 0,9 * E * I_x ) * q^н / q =

             = 0,1*332*10⁵*11.2*10² / (0,9*2,1*10⁶*967*10³) * 5.61/6.68 = 1/588 < [ f / l ] = 1/400 → прочность обеспечена

Проверки местной устойчивости

5.9.1. Проверка местной устойчивости пояса

b_ef / t_f ≤ 0,5 * √ E / R_y

Величина неокаймленного свеса

b_ef = 0,5*(45-1) = 22 см

22 / 2,0 = 11 < 0,5*√ 2,1*10⁶ / 2350 = 14,9 → устойчивость пояса обеспечена

5.9.2. Проверка местной устойчивости стенки

а) Расстановка ребер жесткости

Предусматриваем парные поперечные (вертикальные) ребра в местах опирания балок настила и на опорах.

Так как λ_w = 4,35 > 3,2 , то согласно пункту 7.10 СНиП II – 23 – 81*, расстояние между ребрами

а = 190 (180) см < 2 * h_ef  = 2*130 = 260 см → условие выполнено.

б) Определение размеров промежуточных ребер по СНиП II – 23 – 81*

Требуемая ширина

b_h^тр = h_ef /30 + 40 = 1300/30+40 = 83.3 мм

Принимаем b_h=90 мм > b_h^тр=83.3 мм

 

Требуемая толщина ребра

t_s^тр = 2 * b_h * √ R_y / E = 2*90*√ 2350 / (2,1*10⁶) = 6,02 мм

Тогда b_h х t_s = 90 х 7 мм

Так как принято сопряжение на одном уровне, то размеры ребра : b_h = 110 мм;

                                                                                       t_s = 10 мм.

Принимаем b_h х t_s = 110 х 10 мм.

в) Проверка местной устойчивости стенки

Так как λ_w = 4,35 > 3,5, то проверяем местную устойчивость.

1. Проверка устойчивости стенки в I отсеке

При а/ h_ef =190(180)/130=1.46(1,38)>1 расчётная длина l^р_отс= h_ef =130см

Так как во I отсеке сечение балки не меняется, то вычисляем изгибающий момент М и поперечную силу Q на расстоянии Х₁ = а – h_w / 2 = 1,8 – 0,5*1,30 = 1,15м.

Поперечная сила

Q_{х =}  = 97 т

Изгибающий момент

М_{х =1,15} = ( R_A – P / 2 ) * Х₁ = Q_max * x₁ = 97*1,15 = 111,5 тм

Нормальное напряжение

σ = M_{х =1,15} * 0,5 * h_w / I_x' = 111,5*10⁵* 0,5*130 / (619*10³) = 1171 кг/см²

Касательное напряжение

τ = Q_{x = 1,155} / ( t_w * h_w ) = 97*10³ / (1,1*130) = 746 кг/см²

Нормальное критическое напряжение для I отсека

C_cr = 30,0 (по таблице 21 СНиП II – 23 – 81*).

σ_cr = C_cr *R_y / λ_w² = 30,0*2350 / 4,35² = 3730 кг/см²

Касательное критическое напряжение для I отсека

Отношение большей стороны отсека к меньшей μ = a / h_w = 180/130 = 1,38.

Меньшая из сторон отсека d = h_w =130 см.

λ_ef = d / t_w * √ R_y / E = 130/1*√2350/(2,1*10⁶) = 4,35

τ_сr = 10,3 * ( 1 + 0,76 / μ² ) * R_s / λ_ef² = 10,3*(1+0,76 / 1,38²)*1360 / 4,35² = 1035 кг/см²

Проверка устойчивости

√ ( σ / σ_cr )² + ( τ / τ_cr )² = √ ( 1171 / 3730 )² + ( 746 /1035 )² = 0,786 < γ_с = 1 → местная устойчивость в I отсеке обеспечена.

2. Проверка устойчивости стенки во II отсеке      

Во II отсеке балка меняет сечение. В месте изменения сечения максимальное нормальное напряжение в стенке.

σ = M_{х =2,47} * 0,5 * h_w / I_x' = 2044 кг/см²

τ = Q_х=2,47 / ( t_w * h_w ) = 448 кг/см²

Так как рассчитываемый отсек имеет те же размеры, что и отсек I, кроме длины, не влияющей на расчет, считаем, что критические напряжения имеют те же значения, тогда:

√ ( 2044 / 3730 )² + ( 448 / 1035 )² = 0,55 < γ_с = 1

3. Проверка устойчивости стенки в III отсеке

Устойчивость обеспечена, так как касательное напряжение t меньше.

Расчет поясных швов

 

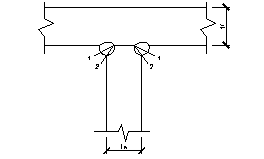
1 – 1 – сечение по металлу шва;

2 – 2 – сечение по металлу границы сплавления.

 

1. Расчет по металлу шва.

Катет шва

Согласно пункту 12.8 СНиП II – 23 – 81* катет шва K_f ≤ 1,2 * t_w = 1,2*1 = 1,2 см.

По таблице 38* СНиП II – 23 – 81* для автоматической сварки при 17 мм < t_f = 20 мм < 22мм катет шва K_f ≥ 6 мм.

Принимаем минимально возможное значение K_f = 6 мм.

По таблице 34* СНиП II – 23 – 81* принимаем автоматическую сварку в «лодочку» при диаметре проволоки d = 1,4 – 2 мм для катета шва K_f = 6 мм.

Коэффициенты, учитывающие форму поперечного сечения шва β_f = 0,9;

   β_z = 1,05.

Коэффициенты условий работы шва γ_wf = γ_wz = 1,0 (пункт 11.2 СНиП II – 23 – 81*).

По таблице 55* СНиП II – 23 – 81* для района II₅, 2-ой группы конструкций и стали С235 принимаем материалы дла сварки: флюс – АН – 348 – А ( по ГОСТ 9087 – 81*);

                            сварочная проволока СВ – 08А ( по ГОСТ 2248 – 70*).

Расчетное сопротивление углового шва срезу по металлу шва

Нормативное сопротивление металла шва по временному сопротивлению R_wun = 4200 кг/см² ( по таблице 4* СНиП II – 23 – 81*).

Коэффициент надежности по металлу шва γ_wm = 1,25 ( по таблице 3*, примечание 3, СНиПII–23–81*).

R_wf = 0,55 * R_wun / γ_wm = 0,55*4200/1,25 = 1850 кг/см²

Расчетное сопротивление по металлу границы сплавления

Временное сопротивление стали разрыву R_un = 3600 кг/см² (по таблице 51* СНиП II – 23 – 81*).

R_wz = 0,45 * R_un = 0,45*3600 = 1620 кг/см²

Условие (*)

1,0 ≤ R_wf / R_wz ≤ β_z / β_f (*)

1,0 < 1848/1620 = 1,14 < 1,05/0,9 = 1,17 → условие выполнено.

Так как условие выполнено, то материал для сварки подобран правильно.

Проверка прочности по металлу шва

Сдвигающее усилие на единицу длины: 

T = Q_max * S_f' / I_x' = 97*10³ * 3300 / (619*10³) = 517 кг.

τ_f = T / (2 * β_f * K_f) = 517 / (2*0,9*0,6) = 478 кг/см²  < R_wf * γ_wf * γ_c = 1850*1,0*1,0 = 1850 кг/см²   → прочность по металлу шва обеспечена.

2. Расчет по металлу границы сплавления.

Так как условие (*) выполнено, и прочность по металлу шва обеспечена, то при γ_wf = γ_wz = 1,0 расчет прочности по металлу границы сплавления даст заведомо положительный результат.

 

Расчет опорных ребер

5.11.1. Конструкция ребер на опорах А и Б.

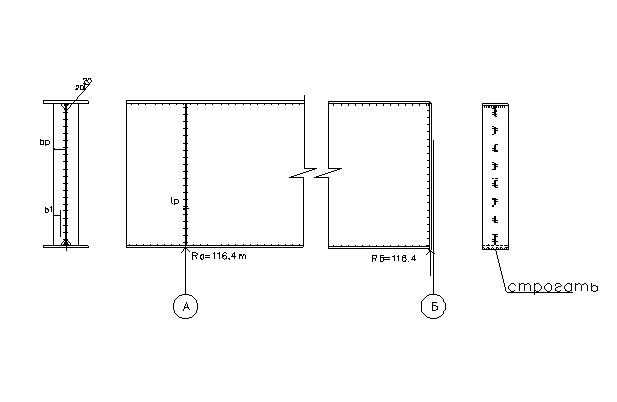
5.11.2. Определение размеров опорных ребер из условия прочности на смятие.

Требуемая ширина ребра на опоре по оси А

b_р^тр = (b_f' – t_w) / 2 = (25-10) / 2 = 12 см = 120 мм

Принимаем b_р = 120 мм.

Длина площадки смятия ребра

b₁ = 1 / 2 *(b_f' – 2 *2,0 - t_w) = 1/2 *(25-2*2,0-1,0) = 10 см

Требуемая толщина ребра по оси А из условия прочности на смятие

Коэффициент надежности по материалу γ_m = 1,025 (по таблице 2* СНиП II – 23 – 81*).

Расчетное сопротивление смятию торцевой поверхности при наличии пригонки

R_p = R_un / γ_m = 3600/1,025 = 3512,2 кг/см².

t_p^тр = R_A / (R_p * 2 * b₁) = 116*10³ / (3512,2*2*10) = 1,58 см

По ГОСТ 82 – 70* принимаем t_p = 1,6 см > t_p^тр = 1,58 см.

Для ребра по оси Б назначаем такую же толщину t_p = 1,6 см, а ширину b_р = b_f' = 25 см, тогда площадь смятия для этого ребра будет больше, чем по оси А, и прочность на смятие заведомо обеспечена.

5.11.3. Расчет опорных ребер на устойчивость в плоскости, перпендикулярной стенке.

S = 0,65 * t_w * √ E / R_y = 0,65*1,0*√2,1*10⁶/2350 = 19,4 см

Так как расчетное сечение по оси Б имеет меньшую площадь, то проверяем устойчивость ребра по оси Б.

A = S * t_w + b_f' * t_p = 19,4*1,0+25*1,6 = 59,4 см²

I_x = t_p * (b_f')³ /12 = 1,6*25³ / 12 = 2083 см⁴

i_x = √ I_x / A = √ 2083 / 59,4 = 5,92 см

λ_x = h_w / i_x = 130/5,92 = 22

φ ≈ 0,956 (по таблице 72* СНиП II – 23 – 81*)

σ = R_Б / (φ * А) = 116*10³ / (0,956*59,4) = 1960 кг/см² < R_y = 2350 кг/см² → устойчивость опорных ребер обеспечена.

5.11.4. Расчет сварного шва, соединяющего спарное ребро по оси Б со стенкой.

По таблице 34* СНиП II – 23 – 81* принимаем полуавтоматическую сварку в углекислом газе проволокой диаметром d < 1,4 мм при нижнем положении шва.

Коэффициенты, учитывающие форму поперечного сечения шва β_f = 0,7;

   β_z = 1,0.

Коэффициенты условий работы шва γ_wf = γ_wz = 1,0 (пункт 11.2 СНиП II – 23 – 81*).

По таблице 55* СНиП II – 23 – 81* для района II₅, 2-ой группы конструкций и стали С235 принимаем сварочную проволоку СВ – 08Г2С ( по ГОСТ 2246 – 70*).

Расчетное сопротивление углового шва срезу по металла шва

Нормативное сопротивление металла шва по временному сопротивлению R_wun = 5000 кг/см² (по таблице 4* СНиП II – 23 – 81*).

Коэффициент надежности по металлу шва γ_wm = 1,25 ( по таблице 3*, примечание 3 ,  СНиП II – 23 –81*).

R_wf = 0,55 * R_wun / γ_wm = 0,55*5000/1,25 = 2200 кг/см²

Расчетное сопротивление по металлу границы сплавления

R_wz = 0,45 * R_un = 0,45*3600 = 1620 кг/см²

Условие (*)

1,0 ≤ R_wf / R_wz ≤ β_z / β_f

1,0 < 2200/1620 = 1,36 < 1,0/0,7 = 1,43 → условие выполнено.

Требуемая высота катета шва

K_f^тр = √ R_Б / (2 * 85 * β_f² * R_wf) = √ (116 *10³) / (2*85*0,7²*2200) = 0,775 см

Принимаем K_f = 0,8 см > K_f^тр = 0,775 см.

При t_p = 16 мм K_f = 0,8 см > K_f,min = 0,5 см и K_f = 0,8 см < K_f,mах = 1,2 * t_w = 1,2*1 = 1,2 см →     условие выполнено.