 |
Главная |
Плоское тело с каналом.
|
из
5.00
|
Рассмотрим плоское тело, свободно двигающееся по гладкой плоскости. Внутри тела вырезан тонкий канал 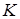 . Пусть в плоскости задана абсолютная система координат
. Пусть в плоскости задана абсолютная система координат  и в точке
и в точке  установлен “столбик”. В начальный момент тело расположено так, что этот столбик попадает в канал
установлен “столбик”. В начальный момент тело расположено так, что этот столбик попадает в канал 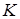 . На движение тела наложена односторонняя связь, состоящая в том, что “столбик” располагается в канале
. На движение тела наложена односторонняя связь, состоящая в том, что “столбик” располагается в канале  . Толщину “столбика” и ширину канала считаем нулевыми.
. Толщину “столбика” и ширину канала считаем нулевыми.
Дадим формальное описание этой системы. Свяжем с телом систему координат  , начало которой
, начало которой  совпадает с центром тяжести тела. Будем считать, что канал
совпадает с центром тяжести тела. Будем считать, что канал 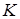 в теле это гладкая кривая, которая задается параметрически
в теле это гладкая кривая, которая задается параметрически
 ,
,  ,
,  (9.1)
(9.1)
где 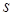 – натуральный параметр, длина вдоль кривой
– натуральный параметр, длина вдоль кривой 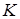 . Сама кривая имеет длину
. Сама кривая имеет длину  . Положение тела можно было бы описывать тройкой координат
. Положение тела можно было бы описывать тройкой координат  , где
, где 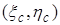 – координаты центра масс тела
– координаты центра масс тела  в абсолютной системе, а
в абсолютной системе, а  – угол наклона оси
– угол наклона оси  связанной системы координат по отношению к оси
связанной системы координат по отношению к оси  абсолютной системы. Однако, мы будем использовать тройку
абсолютной системы. Однако, мы будем использовать тройку  , где
, где  – координаты начала абсолютной системы координат
– координаты начала абсолютной системы координат  в связанной системе. Переход от связанной системы координат к абсолютной производится поворотом на угол
в связанной системе. Переход от связанной системы координат к абсолютной производится поворотом на угол  относительно
относительно  и сдвигом на вектор
и сдвигом на вектор 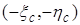 . Поэтому первая и вторая тройки координат связаны соотношениями
. Поэтому первая и вторая тройки координат связаны соотношениями
 (9.2)
(9.2)
а их скорости

Обозначим  – центральный момент инерции тела, а его массу
– центральный момент инерции тела, а его массу  , для краткости записи, будем считать равной единице
, для краткости записи, будем считать равной единице  . По теореме Кенига кинетическая энергия тела
. По теореме Кенига кинетическая энергия тела  выражается соотношением
выражается соотношением
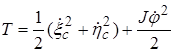 (9.3)
(9.3)
или, в координатах  ,
,

Подставив сюда (9.1) получим лагранжиан системы

где  ,
,  ,
,  . И использовано то, что
. И использовано то, что  – это натуральный параметр и, поэтому,
– это натуральный параметр и, поэтому,  . На систему наложено две односторонних связи:
. На систему наложено две односторонних связи:
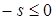 , и
, и  (9.4)
(9.4)
Координата  является циклической и отделяющейся. Циклический интеграл имеет вид
является циклической и отделяющейся. Циклический интеграл имеет вид
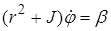
Получаем редуцированную систему с функцией Рауса  :
:

ограничениями (9.4). Это система с одной степенью свободы. Она интегрируется в квадратурах.
Рассмотрим случай абсолютно упругого удара. Для краткости введем обозначение
 ,
, 
Система допускает интеграл энергии  . Положение
. Положение  является положением равновесия, если
является положением равновесия, если  , и реакция связи направлена внутрь допустимой области. Несложно убедиться, последнее условие эквивалентно следующему
, и реакция связи направлена внутрь допустимой области. Несложно убедиться, последнее условие эквивалентно следующему  .
.
Следуя [15], заключаем, что, если последнее неравенство – строгое, то положение равновесия устойчиво. В этом нетрудно убедится прямо. В самом деле, если  , то при увеличении
, то при увеличении  от нуля величина
от нуля величина  будет уменьшаться, а потенциальная энергия
будет уменьшаться, а потенциальная энергия  будет увеличиваться. После удара о связь скорость будет равна
будет увеличиваться. После удара о связь скорость будет равна

В обозначениях предыдущего раздела
 ,
,  ,
, 
поэтому период малых колебаний равен

Все значения берутся при  .
.
Благодарности. Авторы весьма признательны А.П. Иванову, В.В. Козлову, и Д.В. Трещеву за советы и полезные обсуждения данной работы.
ЛИТЕРАТУРА
1. Панагитопулос П.Д. Неравенства в механике. М., Мир, 1986.
2. Козлов В.В., Трещев Д.В. Биллиарды. Генетическое введение в динамику систем с ударами. М., МГУ, 1991.
3. Brogliato B. Nonsmooth Impact Mechanics. Springer-Verlag London Limited, 1996.
4. Иванов А.П. Динамика систем с механическими соударениями. М., “Международная программа образования”, 1997.
5. Вильке В.Г. Аналитическая механика систем с бесконечным числом степеней свободы. М., МГУ, 1997.
6. Schmaedeke W.W. Optimal control theory for nonlinear vector differential equations containing measures. SIAM J. Control, 1965, ser. A, vol. 3, N 2, pp. 231 – 280.
7. Buttazzo G., Percivale D. On the approximation of the elastic bounce problem on Riemanian manifolds. Journal of Differential equations, 1983, 47, 227-275.
8. Козлов В.В. Принципы динамики и сервосвязи. Вестник МГУ, сер. 1, математика, механика. 1989, N 5, с. 59-66.
9. Алексеев В.М. ,Тихомиров В.М., Фомин С.В. Оптимальное управление. М., Наука, 1979.
10. Сорокина О.В., Кугушев Е.И. Принцип Даламбера-Лагранжа в механических системах с односторонними связями. Препринт ИПМ им. М.В. Келдыша РАН, 2002, N 14 .
11. Березинская С.Н., Кугушев Е.И. Об уравнениях движения механических систем с условными односторонними связями. Препринт ИПМ им. М.В. Келдыша РАН, 2002 N 16.
12. Сорокина О.В., Кугушев Е.И. Закономерности движения механических систем с односторонними связями. Препринт ИПМ им. М.В. Келдыша РАН, 2002 N 15.
13. Голубев Ю.Ф. Основы теоретической механики. М., МГУ, 2000. [14] Гирсанов И.В. Лекции по математической теории экстремальных задач. М., МГУ, 1970.
14. Иванов А.П. Об устойчивости в системах с неудерживающими связями. ПММ, 1984, т. 48, вып. 5, с. 725-732.
|
из
5.00
|
Обсуждение в статье: Плоское тело с каналом. |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

