 |
Главная |
Принцип Даламбера-Лагранжа для односторонних связей.
|
из
5.00
|
Содержание
Введение............................................................................................................. 3
1. Принцип Даламбера-Лагранжа для односторонних связей....................... 3
2. Основные законы динамики......................................................................... 7
3. Уравнения Лагранжа 2-го рода................................................................... 9
4. Циклические интегралы и теорема Рауса.................................................. 11
5. Система с условными связями.................................................................... 12
6. Односторонний конек................................................................................. 14
7. Удар в неголономной системе.................................................................... 15
8. Удар о неголономную связь....................................................................... 15
9. Малые колебания........................................................................................ 16
10. Плоское тело с каналом........................................................................... 17
ЛИТЕРАТУРА................................................................................................. 20
Введение
При исследовании механических систем с односторонними связями и импульсными воздействиями с успехом используется аппарат обобщённых функций и функций с ограниченным изменением [1-5]. Следуя этому, будем считать траектории движения абсолютно непрерывными функциями, скорости которых представляет собой функции ограниченного изменения. Это обуславливается тем, что пространство функций с ограниченным изменением является простейшим банаховым пространством содержащим функции скачков, которые характерны для изменения скорости в системах с ударами. Уравнения движения при этом приобретают форму уравнений с мерами Лебега-Стилтьеса [3, 6], или, иначе говоря, обыкновенных дифференциальных уравнений с импульсными правыми частями. Их удобство состоит, в том, что они позволяют описывать движение на всем его протяжении, включающем как безударные участки, так и точки удара, а также участки движения по границе односторонних связей.
Для натуральных механических систем c односторонними связями методом штрафных функций в [7] выведены уравнения движения с мерами в форме уравнений Лагранжа второго рода. В данной работе предлагается способ вывода уравнений движения механических систем общего вида основанный на общепринятом в механике аппарате возможных перемещений и принципе Даламбера-Лагранжа, сформулированных в интегральной форме подобно тому, как это делалось в [8]. Это позволяет для систем с идеальными двухсторонними и односторонними связями получить уравнения движения с мерами в форме уравнений Лагранжа первого рода. Такие уравнения пригодны как для голономных, так и для неголономных систем. Из них выводятся основные законы механики таких систем, а также уравнения движения в форме уравнений Лагранжа второго рода.
Принцип Даламбера-Лагранжа для односторонних связей.
Помимо систем с обычными односторонними связями мы рассмотрим системы с неголономными, и т.н. условными односторонними связями. Односторонними неголономными связями мы называем такие ограничения, накладываемые на движение системы, которые не представлены (и, может быть, не представимы) в виде задания какой-либо области в конфигурационном пространстве. Пример таких ограничений – это линейные ограничения, задаваемые неравенствами вида 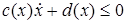 . Они возникают, при описании движения одностороннего конька.
. Они возникают, при описании движения одностороннего конька.
Другой вид подобных ограничений – это т.н. условные связи, возникающие, например, при соударении абсолютно шероховатых поверхностей, которые прокатываются друг по другу без проскальзывания. Формально подобные ограничения можно описать системой: 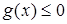 всегда, и
всегда, и 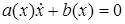 , при
, при 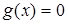 . Первое условие запрещает взаимное проникновение тел, а второе описывает качение без проскальзывния при их соприкосновении.
. Первое условие запрещает взаимное проникновение тел, а второе описывает качение без проскальзывния при их соприкосновении.
Перейдем теперь к общему описанию. Рассмотрим систему из 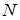 материальных точек, перемещающихся в пространстве под действием приложенных к ним сил. Координаты точек объединим в вектор
материальных точек, перемещающихся в пространстве под действием приложенных к ним сил. Координаты точек объединим в вектор 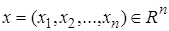 ,
, 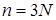 . Введём диагональную
. Введём диагональную 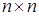 матрицу масс
матрицу масс 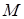 . На её диагонали располагаются массы точек системы, по три одинаковых значения для каждой точки.
. На её диагонали располагаются массы точек системы, по три одинаковых значения для каждой точки.
В отсутствии связей движение системы описывается вторым законом Ньютона
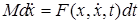
где 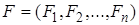 – сводный вектор сил, действующих на точки системы.
– сводный вектор сил, действующих на точки системы.
Наложим на систему семейство 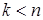 линейных удерживающих связей:
линейных удерживающих связей:
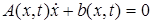
где 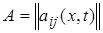 –
– 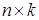 матрица удерживающих связей,
матрица удерживающих связей, 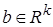 .
.
Добавим к ним семейство 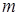 односторонних голономных связей
односторонних голономных связей
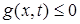
где 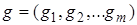
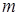 -мерная вектор-функция,
-мерная вектор-функция,  . Здесь и ниже подобные неравенства надо понимать как покоординатное выполнение неравенств:
. Здесь и ниже подобные неравенства надо понимать как покоординатное выполнение неравенств: 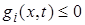 ,
, 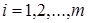 .
.
Наложим на систему также семейство 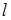 неголономных односторонних связей:
неголономных односторонних связей:
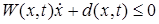
где 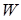 – матрица
– матрица 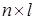 ,
, 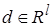 .
.
Добавим также одну группу 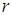 условных связей:
условных связей:
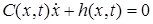
при 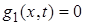 , где
, где 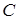 – матрица
– матрица 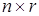 ,
, 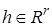 . Мы полагаем, что
. Мы полагаем, что 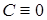 при
при 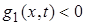 . Рассмотрение систем, где число групп условных связей больше одной, может быть произведено аналогично.
. Рассмотрение систем, где число групп условных связей больше одной, может быть произведено аналогично.
Введем 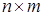 матрицу односторонних связей
матрицу односторонних связей 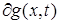 . Строка
. Строка 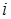 этой матрицы – это вектор
этой матрицы – это вектор 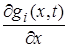 , если
, если 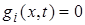 , и нулевой вектор, если
, и нулевой вектор, если 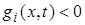 .
.
Определим также  матрицу
матрицу 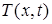 касательного оператора. Она составлена (сверху – вниз) из строк матрицы удерживающих связей
касательного оператора. Она составлена (сверху – вниз) из строк матрицы удерживающих связей 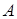 и строк матриц односторонних и условных связей
и строк матриц односторонних и условных связей 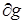 ,
, 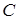 и
и 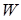 . Мы считаем, что эта матрица имеет максимальный ранг (если отбросить заведомо нулевые строки).
. Мы считаем, что эта матрица имеет максимальный ранг (если отбросить заведомо нулевые строки).
Пространством возможных перемещений 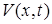 в точке
в точке 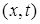 назовем множество векторов
назовем множество векторов 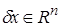 , удовлетворяющих условиям
, удовлетворяющих условиям
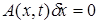 ,
, 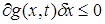 ,
,  ,
, 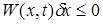
Пространством касательных перемещений 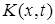 в точке
в точке 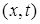 назовем множество векторов
назовем множество векторов 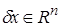 , удовлетворяющих условию
, удовлетворяющих условию
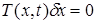
Любое касательное перемещение является возможным.
Следуя [8] будем формулировать условия идеальности связей в интегральной форме. Вариацией кривой 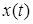 ,
, 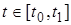 будем называть любую непрерывную вектор-функцию
будем называть любую непрерывную вектор-функцию 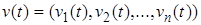 . Вариация
. Вариация 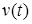 называется возможной, если
называется возможной, если 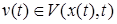 для всех
для всех 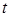 . Вариация
. Вариация 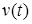 называется касательной, если
называется касательной, если 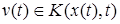 для всех
для всех 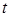 . Поскольку
. Поскольку 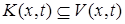 , то любая касательная вариация является возможной. Если вариация
, то любая касательная вариация является возможной. Если вариация 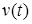 является касательной, то вариация
является касательной, то вариация 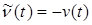 также касательная.
также касательная.
Принцип освобождения от связей. Пусть 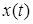 – траектория движения. Тогда систему можно освободить от связей и добавить некую силу – реакцию связей
– траектория движения. Тогда систему можно освободить от связей и добавить некую силу – реакцию связей 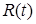 таким образом, что
таким образом, что 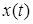 останется траекторией движения освобожденной системы. При этом компоненты реакции связей представляют собой меры Лебега-Стилтьеса
останется траекторией движения освобожденной системы. При этом компоненты реакции связей представляют собой меры Лебега-Стилтьеса 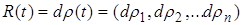 . Они могут иметь особенности, сосредоточенные на множестве тех моментов времени, в которые траектория
. Они могут иметь особенности, сосредоточенные на множестве тех моментов времени, в которые траектория 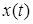 выходит на односторонние ограничения. Траектория системы представляет собой такую абсолютно непрерывную функцию
выходит на односторонние ограничения. Траектория системы представляет собой такую абсолютно непрерывную функцию 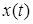 , производная которой,
, производная которой, 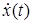 , является функцией с ограниченной вариацией. При этом будут выполнены уравнения движения с мерами.
, является функцией с ограниченной вариацией. При этом будут выполнены уравнения движения с мерами.
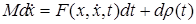 (1.1)
(1.1)
Идеальность связей. Связи называются идеальными, если для любой траектории системы 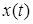 , и для любой её возможной вариации
, и для любой её возможной вариации 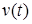 интегральная элементарная работа сил реакции связей неотрицательна, т.е.
интегральная элементарная работа сил реакции связей неотрицательна, т.е.
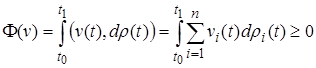 (1.2)
(1.2)
Это условие, в частности, означает, что, при выходе траектории системы на границу удерживающих связей, реакция связей направлена внутрь области, допустимой этими связями.
Из (1.2) следует, что для любой касательной вариации 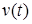 интегральная элементарная работа сил реакции связей равна нулю
интегральная элементарная работа сил реакции связей равна нулю 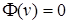 . Если допустить противное, то найдется касательная вариация
. Если допустить противное, то найдется касательная вариация 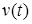 такая, что
такая, что 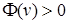 . Взяв касательную и, следовательно, возможную вариацию
. Взяв касательную и, следовательно, возможную вариацию 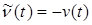 получим
получим 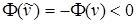 , что противоречит (1.2).
, что противоречит (1.2).
Найдя 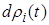 из (1.1) и подставив в (1.2) получим эквивалентную форму записи условия идеальности связей. На траекториях системы для любой возможной вариации
из (1.1) и подставив в (1.2) получим эквивалентную форму записи условия идеальности связей. На траекториях системы для любой возможной вариации 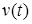 должно выполняться
должно выполняться
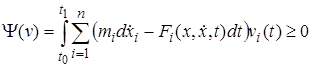 (1.3)
(1.3)
Отсюда следует, что для любой касательной вариации 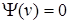 .
.
Сформулируем теперь известное утверждение из функционального анализа, необходимое для вывода уравнений движения нашей системы.
Для заданного движения 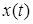 обозначим
обозначим 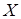 – банахово пространство вариаций
– банахово пространство вариаций 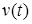 , т.е., пространство непрерывных
, т.е., пространство непрерывных 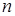 -мерных вектор-функций. Определим на
-мерных вектор-функций. Определим на  касательный оператор
касательный оператор 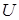 как отображение в пространство
как отображение в пространство 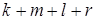 мерных непрерывных функций:
мерных непрерывных функций: 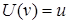 , где
, где 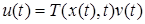 . Обозначим
. Обозначим 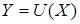 . Это также банахово пространство. Пространство касательных вариаций
. Это также банахово пространство. Пространство касательных вариаций 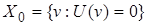 является ядром линейного оператора
является ядром линейного оператора 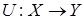 . В соответствии с леммой об аннуляторе ядра регулярного оператора (см., например, [9]) имеем
. В соответствии с леммой об аннуляторе ядра регулярного оператора (см., например, [9]) имеем 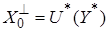 . Здесь символом
. Здесь символом 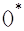 обозначены сопряженные пространства и сопряженные операторы, а
обозначены сопряженные пространства и сопряженные операторы, а 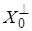
 – аннулятор множества
– аннулятор множества 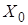 , т.е. множество линейных функционалов обращающихся на нем в ноль.
, т.е. множество линейных функционалов обращающихся на нем в ноль.
Из теоремы Рисса о виде линейного функционала в пространстве непрерывных функций вытекает следующее утверждение: пусть 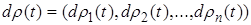 векторная мера Лебега Стилтьеса на
векторная мера Лебега Стилтьеса на 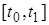 , и
, и
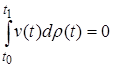
для любой непрерывной вектор-функции 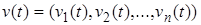 такой, что
такой, что 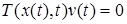 для всех
для всех 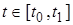 . Тогда найдется мера Лебега-Стилтьеса
. Тогда найдется мера Лебега-Стилтьеса 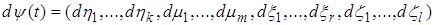 на
на 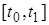 , такая что
, такая что
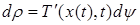
где 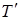 – транспонированная матрица
– транспонированная матрица 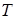 . При этом каждая компонента
. При этом каждая компонента 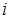 меры
меры 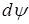 сосредоточена на том множестве, где не обращается в ноль строка
сосредоточена на том множестве, где не обращается в ноль строка 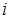 матрицы касательного оператора
матрицы касательного оператора 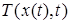 .
.
Разделяя этот оператор на составляющие удерживающих и односторонних связей, получаем
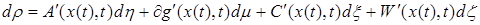 (1.4)
(1.4)
Более подробно с этими вопросами можно ознакомиться в [14].
Принцип Даламбера-Лагранжа. Пусть абсолютно непрерывная кривая 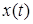 удовлетворяет идеальным связям, наложенным на систему, а ее производная существует почти всюду и является функцией ограниченного изменения. Кривая
удовлетворяет идеальным связям, наложенным на систему, а ее производная существует почти всюду и является функцией ограниченного изменения. Кривая 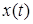 является траекторией движения тогда и только тогда, когда для любой возможной вариации
является траекторией движения тогда и только тогда, когда для любой возможной вариации 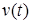 выполнены соотношения (1.3).
выполнены соотношения (1.3).
Применив (1.4) для касательных вариаций получаем отсюда уравнения Лагранжа 1-го рода [10, 11]. Кривая  является траекторией движения системы с идеальными связями (1.1-2) тогда и только тогда, когда найдутся такие векторные меры Лебега-Стилтьеса
является траекторией движения системы с идеальными связями (1.1-2) тогда и только тогда, когда найдутся такие векторные меры Лебега-Стилтьеса 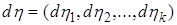 ,
, 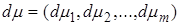 ,
, 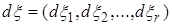 и
и 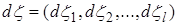 , что
, что
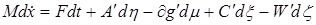 (1.5)
(1.5)
где знак 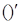 означает транспонирование матриц. При этом каждая мера
означает транспонирование матриц. При этом каждая мера 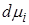 и
и 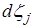 неотрицательна и сосредоточена на множестве моментов времени, в которые
неотрицательна и сосредоточена на множестве моментов времени, в которые 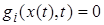 и
и 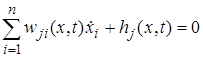 соответственно. Каждая мера
соответственно. Каждая мера 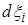 сосредоточена на множестве моментов времени, в которые
сосредоточена на множестве моментов времени, в которые 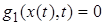 . Неотрицательность мер
. Неотрицательность мер 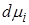 ,
, 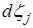 следует из условия идеальности связей (1.2).
следует из условия идеальности связей (1.2).
Функции 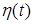 ,
, 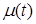 ,
, 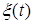 , и
, и 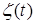 , как функции ограниченной вариации, однозначно раскладываются на сумму трех функций – абсолютно непрерывной, непрерывной сингулярной и функции скачков. Последняя представляет собой ступенчатую функцию с не более чем счетным числом ступеней. В точках скачка мер (и только в них) траекторная скорость
, как функции ограниченной вариации, однозначно раскладываются на сумму трех функций – абсолютно непрерывной, непрерывной сингулярной и функции скачков. Последняя представляет собой ступенчатую функцию с не более чем счетным числом ступеней. В точках скачка мер (и только в них) траекторная скорость 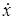 также может иметь скачок. Обозначим эти скачки соответственно
также может иметь скачок. Обозначим эти скачки соответственно 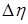 ,
, 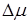 ,
, 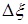 ,
, 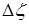 и
и 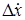 . В силу (1.5) они связаны соотношением
. В силу (1.5) они связаны соотношением
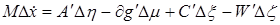
Отсюда, заметив, что во все время движения выполнены уравнения удерживающих связей, т.е. 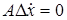 , получаем условие скачка
, получаем условие скачка
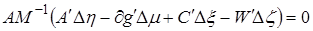
Заметим, что, если функции, описывающие связи, имеют второй класс гладкости, то скорость движения имеет только две составляющие – абсолютно непрерывную функцию и функцию скачков [10].
|
из
5.00
|
Обсуждение в статье: Принцип Даламбера-Лагранжа для односторонних связей. |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

