Индивидуальные задания для АСР. Вариант 26, 27, 28

Вариант 26

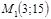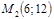1. Написать уравнение прямой, проходящей через две точки  и . Привести его к общему виду.

2. Найти уравнение прямой, проходящей через точку :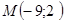

а) параллельно прямой ;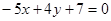

б) перпендикулярно прямой .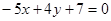

Построить полученные прямые.

3. Привести кривую второго порядка к каноническому виду и построить ее .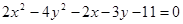

4. Найти точку пересечения прямой 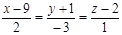 и плоскости .

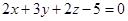5. Найти расстояние от точки 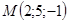 до плоскости .

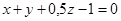6. Найти угол между плоскостью 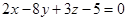 и прямой .

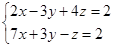7. Найти первые частные производные 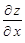 и 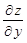 для функции .

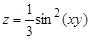8. Найти все частные производные второго порядка для функции .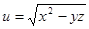

9. Вычислить полный дифференциал 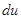 для функции .

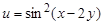10. Исследовать на экстремум функцию

.

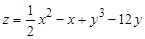11. Нарисовать область интегрирования и вычислить интеграл

.

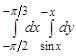12. С помощью двойного интеграла вычислить площадь фигуры, ограниченной линиями

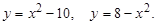
13. Вычислить производную функции 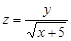 в точке А  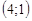по направлению к точке В  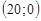и 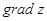 в точке В.

Вариант 27

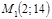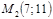1. Написать уравнение прямой, проходящей через две точки  и . Привести его к общему виду.

2. Найти уравнение прямой, проходящей через точку :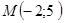

а) параллельно прямой ;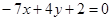

б) перпендикулярно прямой .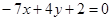

Построить полученные прямые.

3. Привести кривую второго порядка к каноническому виду и построить ее .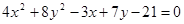

4. Найти точку пересечения прямой 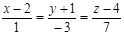 и плоскости .

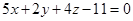5. Найти расстояние от точки 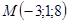 до плоскости .

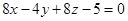6. Найти угол между плоскостью 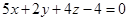  и прямой .

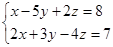7. Найти первые частные производные 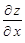 и 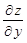 для функции .

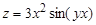8. Найти все частные производные второго порядка для функции .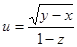

9. Вычислить полный дифференциал 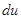 для функции

.

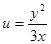10. Исследовать на экстремум функцию

.

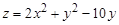11. Нарисовать область интегрирования и вычислить интеграл

.

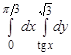12. С помощью двойного интеграла вычислить площадь фигуры, ограниченной линиями

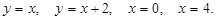
13. Вычислить производную функции 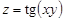 в точке А  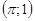по направлению к точке В  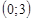и 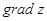 в точке В.

Вариант 28

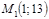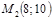1. Написать уравнение прямой, проходящей через две точки  и . Привести его к общему виду.

2. Найти уравнение прямой, проходящей через точку :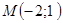

а) параллельно прямой ;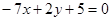

б) перпендикулярно прямой .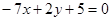

Построить полученные прямые.

3. Привести кривую второго порядка к каноническому виду и построить ее .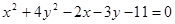

4. Найти точку пересечения прямой 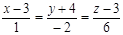 и плоскости .

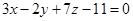5. Найти расстояние от точки 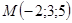 до плоскости .

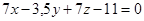6. Найти угол между плоскостью 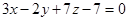  и прямой  .

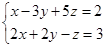7. Найти первые частные производные 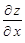 и 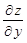 для функции .

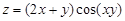8. Найти все частные производные второго порядка для функции .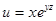

9. Вычислить полный дифференциал 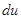 для функции

.

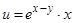10. Исследовать на экстремум функцию

.

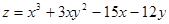11. Нарисовать область интегрирования и вычислить интеграл

.

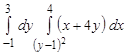12. С помощью двойного интеграла вычислить площадь фигуры, ограниченной линиями

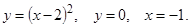
13. Вычислить производную функции 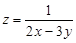 в точке А  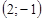по направлению к точке В  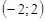и 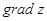 в точке В.