 |
Главная |
ПРИМЕР РЕШЕНИЯ ЗАДАЧИ №5
|
из
5.00
|
Требуется построить эпюры поперечных сил и изгибающих моментов и подобрать размеры поперечного сечения стальной балки (Рисунок 16) для различных форм сечения: двутавровой балки, балки прямоугольного сечения со сторонами h и b при h/b = 2 и круглого поперечного сечения. Балка выполнена из стали с допускаемым напряжением [s ] =190МПа;
а =1 м; q=10кН/м.
|
|

|

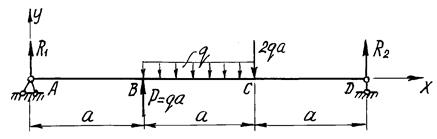
Рисунок 16 - Расчетная схема балки
1.Определение опорных реакций.
На схеме показываем опорные реакции R1, H, R2 . Вертикальные реакции направляем вверх и записываем уравнения равновесия:
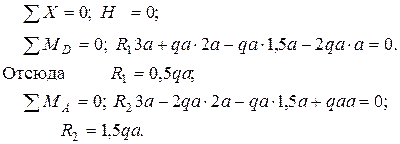
Проверим правильность вычислений, составив еще одно уравнение равновесия:

Условие равновесия удовлетворяется, реакции определены правильно.
2.Построение эпюры Q.
Мысленно разбиваем балку на участки. Границами участков являются сечения, в которых к балке приложены сосредоточенные силы или пары сил, начинаются или заканчиваются распределенные нагрузки, имеются промежуточные шарниры. В рассматриваемой балке граничными сечениями будут сечения A, B, C и D. Для каждого из трех участков запишем аналитическое выражение Q (x).
Участок AB, 0<x<a.Рассмотрим произвольно выбранное сечение с абсциссой x. Рассекая балку в этом сечении на две части и отбросив правую часть, вычисляем алгебраическую сумму проекций на ось y всех сил, действующих на оставшуюся часть:
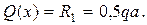
Поперечная сила не зависит от переменной x на протяжении всего участка, следовательно, эпюра Q ограничена прямой, параллельной оси абсцисс. Отложив от оси эпюры вверх в выбранном масштабе 0,5qa (Рисунок 17), строим эпюру на этом участке.
Участок BC,a<x<2a.Алгебраическая сумма проекций всех сил на ось y слева от сечения с абсциссой x
 .
.
Полученное выражение является уравнением наклонной прямой, которая может быть построена по двум лежащим на ней точкам. Для ее построения найдем значения поперечной силы на границах участков балки

Участок CD, 2a<x<3a. Поперечная сила на расстоянии x от начала координат
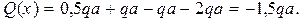
Так как поперечная сила не зависит от переменной x, на последнем участке эпюра Q ограничена прямой, параллельной оси балки (см. рисунок 17).
3. Построение эпюры Mz.
Аналитическое выражение для вычисления изгибающего момента в сечении x необходимо записать для каждого участка балки.
Участок AB:
 .
.
На этом участке балки изгибающий момент возрастает по линейному закону и эпюра Mz ограничена наклонной прямой. Вычисляя его значения в сечениях на границах участка, строим в масштабе (рисунок 17) эпюру Mz на сжатом волокне
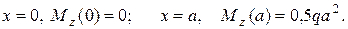
Участок BC:

Полученное уравнение является уравнением квадратной параболы и, поскольку поперечная сила Q на участке BC не изменяет знак, экстремума на эпюре Mz не будет.
Определим изгибающий момент на границах участка:


Отложив вверх от оси балки найденные значения, проводим квадратную параболу выпуклостью вверх (навстречу вектору усилия равномерно распределенной нагрузки).
Участок CD:
 .
.
В пределах последнего участка балки (2a<x<3a) изгибающий момент линейно зависит от абсциссы x, и эпюра ограничена прямой линией.
При  при
при 
 Эпюры Q и Mz показаны на Рисунок 17.
Эпюры Q и Mz показаны на Рисунок 17.

|
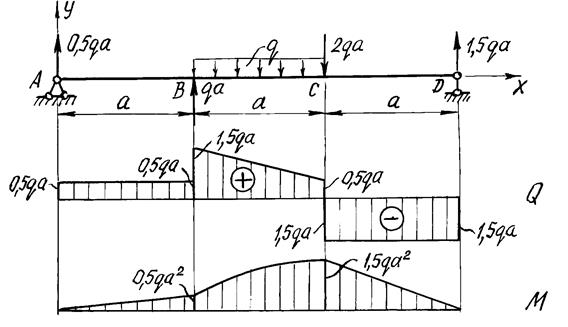
Рисунок 17 - Расчетная схема балки. Эпюры поперечных сил и изгибающих моментов
По эпюре Mz находим опасное сечение балки - сечение, в котором изгибающий момент максимален по абсолютной величине. Для заданной балки изгибающий момент в опасном сечении 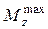 = Mz(2a)=1,5qa2 или после подстановки числовых значений
= Mz(2a)=1,5qa2 или после подстановки числовых значений  15кН×м.
15кН×м.
Из условия прочности определим требуемый момент сопротивления сечения

Номер двутавра находим по расчетному значению момента сопротивления Wz, используя таблицы сортамента прокатной стали.
Внимание! В таблицах сортамента прокатной стали (см. приложение) оси z соответствует ось x , это означает, что  .
.
Наиболее близок к требуемому момент сопротивления двутавра №14,
равный Wx=81,7 см3. Выбрав это сечение, определяем нормальные напряжения в поперечном сечении балки:

Подбираем прямоугольное сечение, момент сопротивления которого определяется с учетом того, что 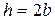 :
:

Отсюда

Круглое поперечное сечение имеет момент сопротивления
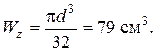
Диаметр круга

Рассмотрим второй метод построения эпюр внутренних усилий, действующих в сечениях балки. Он состоит в том, что поперечные силы и изгибающие моменты вычисляются на границах участков без записи уравнений  , а соответствующие эпюры строятся на основании дифференциальных зависимостей между Q, M, q:
, а соответствующие эпюры строятся на основании дифференциальных зависимостей между Q, M, q:
 . (5.3)
. (5.3)
Зависимости (5.3) позволяют установить следующие характерные особенности эпюр поперечных сил и изгибающих моментов:
На участках, где нет распределенной нагрузки, эпюра Q ограничена прямыми, параллельными оси балки, а эпюра M - наклонными прямыми.
На участках, где приложена равномерно распределенная нагрузка интенсивностью q, эпюра Q ограничена наклонными прямыми, а эпюра M - квадратными параболами, выпуклость которых направлена навстречу вектору равномерно распределенной нагрузки.
На участках, где Q >0, изгибающий момент возрастает; если Q<0 - изгибающий момент убывает.
В сечениях, где к балке приложены сосредоточенные силы, на эпюре Q будут скачки на величину приложенных сил, а на эпюре M - переломы, острие которых направлено против действия этих сил.
В сечениях, где к балке приложены пары сил (сосредоточенные моменты), на эпюре M будут скачки на величину этих моментов.
Если на участке балки имеется равномерно распределенная нагрузка и эпюра Q в пределах участка изменяет знак, то в сечении, где Q = 0, на эпюре Mz будет экстремум.
Примеры использования дифференциальных зависимостей при расчете балок приводятся ниже.
Рассмотрим задачу подбора сечения балки, изготовленной из хрупкого материала. Балка (Рисунок18) изготавливается из чугуна и имеет сечение, показанное на Рисунке 20.
Требуется определить из расчета на прочность по допускаемым напряжениям размеры поперечного сечения, если материал балки - чугун с допускаемым напряжением на сжатие [s]сж=700МПа и на растяжение[s]р=140МПа;  1м;
1м;  10кН/м.
10кН/м.

Рисунок 18 - Расчетная схема чугунной балки
Для нахождения опасного сечения строим эпюры M и Q. Очевидно, что данная балка имеет три участка:
AB (0 
 ), BC (a
), BC (a 
 ), CD (2a
), CD (2a 
 ).
).
Для того чтобы не вычислять опорные реакции, рассмотрим балку, начиная с участка AB. Найдем поперечную силу и изгибающий момент в начале этого участка. Мысленно рассечем балку в сечении A на две части и отбросим правую ее часть. Слева на оставшуюся часть действует только сосредоточенная сила, равная 2qa. Проектируя эту силу на нормаль к оси балки, получаем
Q(0) = 2qa.
Рассекая балку в сечении B и поступая аналогично, находим величину поперечной силы в этом сечении - она равна алгебраической сумме проекций сил, действующих на оставшуюся левую часть балки, на нормаль к ее оси:
Q(a) = 2qa - qa  qa,
qa,
где 2qa - проекция сосредоточенной силы на нормаль к оси балки;
qa - проекция равнодействующей распределенной нагрузки.
Изгибающий момент в начале первого участкаM (0) = 0; в конце участка он равен алгебраической сумме моментов относительно точки B от сосредоточенной силы 2qa и распределенной нагрузки:
 .
.
Строим эпюры Q и Mz для первого участка балки.
Выбрав масштаб, откладываем вверх от оси эпюр (Q и Mz положительны!) найденные значения поперечных сил и изгибающих моментов. На эпюре Q соединяем прямой линией точки с координатами (0, 2qa) и (a, qa), а на эпюре Mz проводим квадратную параболу выпуклостью вверх через точки (0, 0) и(a, 1,5qa2).
Поступая аналогично, вычисляем поперечные силы и изгибающие моменты в начале и конце участков BC и CD.
Участок BC:  ;
;
Q (a)  qa, Q (2a)
qa, Q (2a)  qa;
qa;
M (a)  1,5qa2, M (2a)
1,5qa2, M (2a)  2,5qa2.
2,5qa2.
Отложив вверх вычисленные значения Q и M, строим эпюры внутренних усилий на втором участке балки. Как следует из дифференциальных зависимостей, эти эпюры ограничены прямыми линиями.
Участок CD:  ;
;
Q (2a)  qa, Q (3a)
qa, Q (3a)  qa;
qa;
M (2a) =4,5qa2, M (3a)=5,5qa2.
В начале последнего участка к балке приложена пара сил, что вызывает появление скачка на эпюре изгибающих моментов. На участке CD распределенной нагрузки нет, поэтому эпюры Q, Mz ограничены прямыми линиями (Рисунок 19).
Окончательный вид эпюр Q, Mz показан на том же рисунке.

Рисунок 19 - Расчетная схема балки. Эпюры поперечных сил и изгибающих моментов
Опасное сечение находится в заделке и расчетный изгибающий момент  = 5,5qa2 =
= 5,5qa2 =  Н×м =
Н×м = 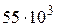 Н×м= 55 кН×м.
Н×м= 55 кН×м.
Для определения размеров поперечного сечения необходимо найти из условия прочности балки осевой момент сопротивления относительно его нейтральной оси.
Заданное сечение (Рисунок 20) имеет ось симметрии, и для определения положения его центра тяжести достаточно вычислить только одну его координату- ординату ус.
Разобьем заданную фигуру на две простые части: прямоугольник (1) и полукруг (2). В качестве исходных осей принимаем главные центральные оси прямоугольника y1, z1. Тогда ордината центра тяжести всей фигуры определится по формуле
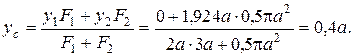
Определив положение центра тяжести, проводим главные центральные оси 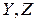 составной фигуры.
составной фигуры.

Рисунок 20 - Поперечное сечение чугунной балки
Вычисляем момент инерции заданного сечения относительно главной центральной оси Z*):

При расчете на прочность балок, изготовленных из хрупких материалов, для сечений с одной осью симметрии необходимо вычислять два момента сопротивления относительно оси Z:

Из эпюры изгибающих моментов (Рисунок 20), построенной на сжатом волокне, следует, что в опасном сечении верхние волокна балки сжаты, а нижние растянуты. Условие прочности для опасных точек в растянутой зоне сечения имеет вид
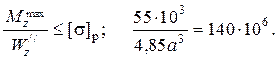
Отсюда a = 0,043м = 4,3 см.
Опасной точкой в сжатой зоне является точка, наиболее удаленная от оси z на расстояние  . Условие прочности балки по допускаемым напряжениям на сжатие
. Условие прочности балки по допускаемым напряжениям на сжатие

Отсюда a = 0,026м = 2,6см.
В расчете по нормальным напряжениям из двух найденных значений a принимаем большее (a = 4,3см), что обеспечивает прочность материала балки как в растянутой, так и в сжатой зонах.
Рассмотрим пример подбора составного сечения стальной балки.
Для балки (Рисунок 21) подобрать сечение, состоящие из двух стальных швеллеров. Принять а = 1 м; q = 10кН/м;[s ] =190МПа.
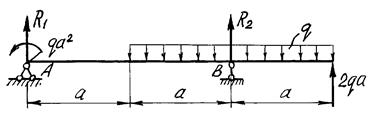
Рисунок 21 - Расчетная схема балки
Определяем опорные реакции:


Отметим, что момент распределенной нагрузки относительно опоры B равен нулю, а реакция второй опоры направлена не вверх, как показано на Рисунок 21, а вниз.
Проверка правильности вычисления опорных реакций:

Реакции определены правильно.
Эпюры Q, Mz строятся аналогично эпюрам предыдущего примера. Вид эпюр показан на Рисунок 22.
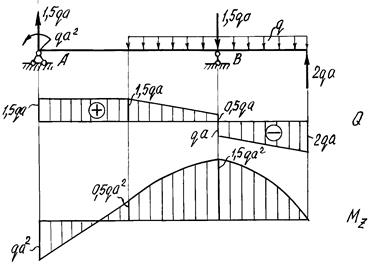
Рисунок 23. Расчетная схема балки. Эпюры поперечных сил и
изгибающих моментов
По эпюре Мz находим величину изгибающего момента, максимального по модулю

Сечение балки подбираем из условия прочности при изгибе. Требуемый момент сопротивления сечения, состоящего из двух швеллеров
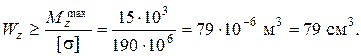
Осевой момент сопротивления одного швеллера будет в два раза меньше- 
По таблице сортамента прокатной стали находим, что ближайший подходящий момент сопротивления имеет швеллер № 12, для которого  Wx= 50,6см3. Швеллер № 10 с осевым моментом сопротивления
Wx= 50,6см3. Швеллер № 10 с осевым моментом сопротивления 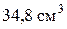 принять нельзя, так как в этом случае момент сопротивления сечения, составленного из двух швеллеров, будет равен 69,6 см3<79 см3 и напряжения в балке превысят допускаемые на 13 %, что неприемлемо (в расчетах допускается перенапряжение £ 5%) .
принять нельзя, так как в этом случае момент сопротивления сечения, составленного из двух швеллеров, будет равен 69,6 см3<79 см3 и напряжения в балке превысят допускаемые на 13 %, что неприемлемо (в расчетах допускается перенапряжение £ 5%) .
Рассмотрим пример решения второй части задачи № 5.
Построим эпюры распределения нормальных напряжений по высоте сечения для двух балок - двутавровой стальной и чугунной.
Нормальные напряжения в поперечном сечении балок при изгибе определяются по формуле (5.1).
По ширине сечения нормальные напряжения распределяются равномерно. Зависимость между s и у линейная, нормальные напряжения прямо пропорциональны расстоянию слоя волокон от нейтральной оси, совпадающей с главной центральной осью инерции Z.
Вычислим максимальные нормальные напряжения в двутавровом сечении балки

Минимальные (сжимающие) напряжения в двутавровом сечении по абсолютной величине будут равны максимальным растягивающим напряжениям.
Для чугунной балки величина максимальных (растягивающих) напряжений
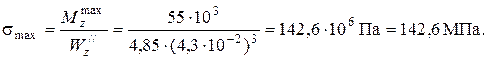
Минимальные (сжимающие) напряжения

Выбрав масштаб, строим эпюры распределения нормальных напряжений по высоте стальной (Рисунок 24, а) и чугунной (Рисунок 24, б) балок.
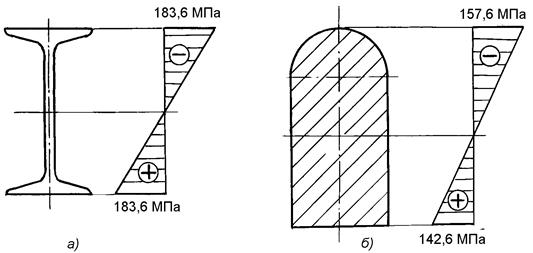
Рисунок 24 - Распределение нормальных напряжений по высоте балок
ЗАДАЧА № 6
Для двух заданных плоских рам построить эпюры изгибающих моментов. Схемы рам и числовые данные для решения задачи выбираются из табл.6 и по рисунку 25.
Таблица 6 - Числовые данные к задаче № 6
| Номер строки | Номер расч. схемы | Сила, кН | Момент, кН×м | Размер а, м | |||
| (рисунок25) | 
| 
| 
| 
| 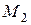
| ||
|
из
5.00
|
Обсуждение в статье: ПРИМЕР РЕШЕНИЯ ЗАДАЧИ №5 |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

