Особенности применения методов параметрической статистики при анализе эмпирических данных

Параметрическая статистика применяется в тех случаях, когда тестовые показатели измерены в интервальной шкале, шкале отношений или абсолютной шкале при соблюдении распределения Гаусса. В данном случае применяются методы анализа данных при помощи моды, медианы и среднего (Мо; Ме; Мх) [меры центральной тенденции], дисперсии и среднего квадратического отклонения (Dх ; δх), коэффициента вариации (V) [меры изменчивости], коэффициента корреляции Пирсона (Rxy)[меры связи], t-критерия Стъюдента, υ-критерия Уэлша, F-критерия Фишера [статистический вывод] и психодиагностического прогнозирования при помощи методов линейной и нелинейной регрессии [модели регрессии].

Статистические методы применяются в определенном доверительном интервале, который задается исходя из потребностей точности измерений. Доверительным интервалом называется интервал (X ± e), который "накрывает" неизвестный параметр с заданной точностью. В биологических и социальных исследованиях максимальное значение e задается в пределах 5%. То есть e £ 0.05.

8) Основной мерой центральной тенденции в параметрическом измерении является среднее значение - математическое ожидание (Мх). Это сумма всех измеренных значений свойства, отнесенное к количеству этих измерений.

9) Изменчивость признаков в параметрических шкалах измеряется при помощи дисперсии и среднего квадратического отклонения (δх). Среднее квадратическое отклонение определяется как арифметическое значение квадратного корня из дисперсии - среднего арифметического квадратов отклонений отдельных значений измеренного свойства от их среднего значения.

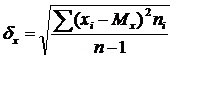
10) Коэффициент корреляции Пирсона (Rxy) показывает наличие статистической связи между психологическими переменными х и у, при которой каждой переменной х соответствует не одно или несколько определенных значений у, а распределение у, меняющееся вместе с изменением х, которое может быть однонаправленным (+) и разнонаправленным (-).

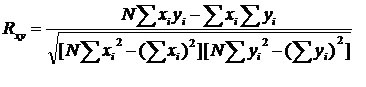
где xi - значение показателя первой переменной;
yi - значение показателя второй переменной;
N - объем выборки.

Теоретическая интерпретация коэффициента корреляции Пирсона Rxy подобна другим статистикам из области измерения связей между переменными. Если значение Rxy более 0.5, то имеет место статистически сильная связь, если менее 0.5 — слабая. Положительные и отрицательные знаки показывают направленность связи (соответственно, прямая и обратная).

11) При определенном количестве измерений (n) корреляционные связи могут быть значимыми и незначимыми. Исследователю необходимо это знать для того, чтобы сделать достоверный вывод о причинно-следственных связях переменных. Уровень значимости коэффициентов корреляции определяется по формуле расчета t-критерия при помощи таблиц "Квантилей t-распределения Стъюдента для доверительной вероятности".

где R — численное значение коэффициента корреляции;
n — объем выборки.

12) Точечный биссериальный коэффициент корреляции Пирсона (Rpb) — метод корреляционного анализа отношения переменных, одна из которых измерена в дихотомической шкале наименований, а другая — в интервальной шкале отношений или порядка. Точечно-биссериальный коэффициент корреляции применяется также для определения дискриминативности заданий тестов.

Rpb = [(Mx — Mо) / δx] √ n1 nо / n (n — 1),

где Mx - среднее по Х объектов со значением 1 по Y;
Mо - среднее по Х объектов со значением 0 по Y;
δ x - стандартное отклонение всех значений по Х;
n1 - число объектов с 1 по Y;
nо - число объектов с 0 по Y;
n - общее число объектов.
Интервал измерения Rpb от –1 до +1. Теоретическая интерпретация значений подобна Rxy.

13) Расчет коэффициентов корреляции является инструментом, позволяющим осуществить корреляционный, факторный и кластерный анализ эмпирических данных.
Корреляционный анализ — метод исследования взаимозависимости признаков в генеральной совокупности, являющихся случайными величинами, имеющими нормальное многомерное распределение. Для наглядности интеркорреляционные показатели представляются в виде таблиц корреляций переменных, матриц и графов.
Факторный анализ — раздел многомерного статистического анализа, сущность которого заключается в выявлении непосредственно неизмеряемого признака, являющегося "главной компонентой" (производной) группы измеренных тестовых показателей.
Кластерный анализ — совокупность статистических (и иных, в том числе качественных) методов, предназначенных для дифференциации относительно отдаленных друг от друга групп и близких между собой объектов по информации о связях (мерах близости) между ними.

14) t-критерий Стъюдента, υ-критерий Уэлша, F-критерий Фишера представляют собой методы статистического вывода о наличии значимой связи между признаками или выявления признака, характеризующего генеральную совокупность. На практике они применяются для оценки подобия двух групп испытуемых, у которых измерены определенные свойства, по средней и дисперсии тестовых данных. t-критерий в отличие от υ-критерия применяется в ситуации равенства средних квадратических отклонений. F-критерий определяет подобие выборок по дисперсии их эмпирических переменных.

где Мх - средние значения тестовых данных;
n - количество испытуемых;
δ - среднеквадратическое отклонение.

Анализ результатов исследования при помощи t -критерия осуществляется по следующему алгоритму:
а) производится расчет значений t-критерия;
б) по количеству испытуемых осуществляется вход в таблицу "Квантилей t-распределения Стъюдента..."(см. табл.);
в) значение расчетного t-критерия (tp) сравнивается с табличным значением (tт);
г) если tp > tт, то выборки значимо различаются на уровне доверительной вероятности;
д) если tp < tт, то группы испытуемых принадлежат одной совокупности.