 |
Главная |
Сила. Система сил. Равновесие абсолютно твердого тела
|
из
5.00
|
СТАТИКА
Глава I. ОСНОВНЫЕ ПОНЯТИЯ И АКСИОМЫ СТАТИКИ
Сила. Система сил. Равновесие абсолютно твердого тела
В теоретической механике изучается движение материальных тел относительно друг друга. Для этого требуется, прежде всего, построить модели объектов и дать определение понятий, с которыми имеет дело механика. В теоретической механике рассматривается простейшая модель "обычного" евклидова трехмерного пространства. Постулируется, что в этом пространстве существует хотя бы одна система координат, в которой справедливы законы Ньютона (инерциальная система). Многочисленные опыты и измерения показывают, что с высокой степенью точности система отсчета с началом в центре Солнечной системы и осями, направленными к "бесконечно удаленным неподвижным" звездам, является инерциальной системой. Если существует хотя бы одна инерциальная система, то их имеется бесчисленное множество. Инерциальная система – это система, в которой действуют законы Ньютона. Инерциальные системы отсчета условно называют неподвижными.
В статике, не внося никаких погрешностей в вычисления, можно считать, что системы координат, жестко связанные с Землей, неподвижны. Условия относительного равновесия в других, неинерциальных системах отсчета, в частности, в системах, движущихся относительно Земли, будут рассмотрены в динамике.
Как для статики, так и для динамики одним из основных является понятие силы. Первичное представление о ней дают наши мускульные ощущения.
В механике под силой понимается мера механического взаимодействия материальных тел, в результате которого взаимодействующие тела могут сообщать друг другу ускорения или деформироваться (изменять свою форму).
Из этого определения сразу вытекают два способа измерения сил:
первый, динамический способ, основан на измерении ускорения тела в инерциальной системе отсчета;
второй, статический способ, основан на измерении деформации упругих тел.
В механике не изучают физическую природу сил. Силы могут возникать при непосредственном контакте тел (например, сила тяги электровоза, передаваемая вагонам, сила трения между поверхностями соприкасающихся тел). Силы возникают и на расстоянии (например, силы притяжения небесных тел, силы взаимодействия электрически заряженных или намагниченных частиц и т.д.).
Сила является векторной величиной – она характеризуется численным значением или модулем, точкой приложения и направлением. 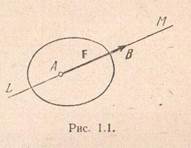 Точка приложения силы и ее направление определяют линию действия силы. На рис. 1.1 показана сила F, приложенная к точке А, длина отрезка АВ в соответствующем масштабе равна модулю силы, точка В называется концом силы; у конца силы; у конца силы ставится стрелка, указывающая направление действия силы. Прямая LM называется линией действия силы. Условимся обозначать силу буквой жирного шрифта, например, F, а ее модуль той же буквой обычного шрифта, т.е. F.
Точка приложения силы и ее направление определяют линию действия силы. На рис. 1.1 показана сила F, приложенная к точке А, длина отрезка АВ в соответствующем масштабе равна модулю силы, точка В называется концом силы; у конца силы; у конца силы ставится стрелка, указывающая направление действия силы. Прямая LM называется линией действия силы. Условимся обозначать силу буквой жирного шрифта, например, F, а ее модуль той же буквой обычного шрифта, т.е. F.
Для измерения модуля силы ее сравнивают с некоторой силой, выбранной в качестве единицы. В международной системе единиц измерения физических величин (СИ) за единицу силы принят один ньютон (1 Н), а в технической системе единиц (система МКГСС) – один килограмм силы (1 кГ или 1 кгс – не следует смешивать с единицей массы в системе СИ – 1 кг). Эти единицы связаны соотношениями
1 кГ ≈ 9,81 Н; 1 Н ≈ 0,102 кГ.
 Рассматривая действие сил на материальные тела, мы будем отвлекаться не только от физической природы сил, но и от многих свойств самих тел. Так, реальные твердые тела обычно мало изменяют свою форму под действием приложенных к ним сил. Поэтому для решения многих задач механики допустимо вовсе пренебречь малыми деформациями (т.е. малыми изменениями формы) и пользоваться моделью абсолютно твердого тела. Под абсолютно твердым телом понимают тело, в котором расстояния между двумя любыми точками его остаются неизменными независимо от действия тех или иных сил. Для краткости мы будем часто применять выражение "твердое тело" или даже просто "тело", имея в виду только что введенное понятие абсолютно твердого тела.
Рассматривая действие сил на материальные тела, мы будем отвлекаться не только от физической природы сил, но и от многих свойств самих тел. Так, реальные твердые тела обычно мало изменяют свою форму под действием приложенных к ним сил. Поэтому для решения многих задач механики допустимо вовсе пренебречь малыми деформациями (т.е. малыми изменениями формы) и пользоваться моделью абсолютно твердого тела. Под абсолютно твердым телом понимают тело, в котором расстояния между двумя любыми точками его остаются неизменными независимо от действия тех или иных сил. Для краткости мы будем часто применять выражение "твердое тело" или даже просто "тело", имея в виду только что введенное понятие абсолютно твердого тела.
 Совокупность нескольких сил (F1,…, Fn) называется системой сил. Если, не нарушая состояния тела, одну систему сил (F1,…, Fn) можно заменить другой системой (P1,…, Pk) и наоборот, то такие системы называются эквивалентными. Символически это обозначается следующим образом:
Совокупность нескольких сил (F1,…, Fn) называется системой сил. Если, не нарушая состояния тела, одну систему сил (F1,…, Fn) можно заменить другой системой (P1,…, Pk) и наоборот, то такие системы называются эквивалентными. Символически это обозначается следующим образом:
(F1,…, Fn) = (P1,…, Pk).
Введенное понятие эквивалентности систем сил не устанавливает условий, при выполнении которых две системы будут эквивалентны. Оно означает только, что эквивалентные системы сил вызывают одинаковое состояние тела (одинаковые ускорения или, если тело не абсолютно твердое, одинаковые деформации).
В том случае, когда система сил (F1,…, Fn) эквивалентна одной силе R, т.е.
(F1,…, Fn) = R, 
последняя называется равнодействующей данной системы сил. Это означает, что одна равнодействующая сила может заменить действие всех данных сил. Не всякая система сил имеет равнодействующую.
Как уже отмечалось, в инерциальной системе координат выполняется закон инерции. Это означает, в частности, что тело, находящееся в начальный момент в покое, остается пребывать в этом состоянии, если на него не действуют никакие другие силы.
Если абсолютно твердое тело остается в состоянии покоя при действии на него системы сил (F1,…, Fn), то последняя называется уравновешенной системой сил или системой сил, эквивалентной нулю:
(F1,…, Fn) = 0.
Часто в этом случае говорят, что тело находится в равновесии.
1.2. Аксиомы статики и их следствия
В аксиомах статики формулируются те простейшие и общие законы, которым подчиняются силы, действующие на одно и то же тело, или силы, приложенные к взаимодействующим телам. Эти законы установлены многочисленными непосредственными наблюдениями, а также проверкой следствий (часто далеких и вовсе не очевидных), логически вытекающих из этих аксиом.
Как следует из второго закона Ньютона, тело под действием одной силы приобретает ускорение и, следовательно, оно не может находиться в покое. Это означает, что одна сила не может составлять уравновешенную систему сил. Первая аксиома устанавливает условия, при выполнении которых простейшая система сил будет уравновешена.
Аксиома 1. Две силы, приложенные к абсолютно твердому телу, будут уравновешены (эквивалентны нулю) тогда и только тогда, когда они равны по модулю, действуют по одной прямой и направлены в противоположные стороны.

Это означает, что если абсолютно твердое тело находится в покое под действием двух сил, то эти силы равны по модулю, действуют по одной прямой и направлены в противоположные стороны. Обратно, если на абсолютно твердое тепло действуют по одной прямой в противоположные стороны две равные силы и тело в начальный момент находилось в покое, то 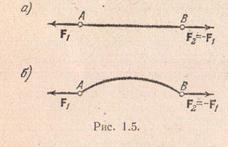 состояние покоя тела сохранится.
состояние покоя тела сохранится.
На рис. 1.4 показаны уравновешенные силы, удовлетворяющие соотношениям: (F1, F2) = 0, (P1, P2) = 0.
При решении некоторых задач статики приходится рассматривать силы, приложенные к концам жестких стержней, весом которых можно пренебречь, причем известно, что стержни находятся в равновесии. Из сформулированной аксиомы непосредственно следует, что на такой стержень силы направлены вдоль прямой, проходящей через концы стержня, противоположны по направлению и равны друг другу по модулю. Этот вывод сохраняется и в случае, если ось стержня криволинейная.
Первая аксиома устанавливает необходимые и достаточные условия уравновешивания только двух сил, но, конечно, уравновешенная система сил может состоять и из большего числа сил.
Две следующие аксиомы устанавливают простейшие действия с силами, при которых состояние тела не изменяется.
Аксиома 2. Не нарушая состояния абсолютно твердого тела, к нему можно прикладывать или отбрасывать силы тогда и только тогда, когда они составляют уравновешенную систему, в частности, если эта система состоит из двух сил, равных по модулю, действующих по одной прямой и направленных в противоположные стороны.

Из этой аксиомы вытекает следствие: не нарушая состояния тела, точку приложения силы можно переносить вдоль линии ее действия.
Это следствие показывает, что сила, приложенная к абсолютно твердому телу, представляет собой скользящий вектор.
Обе аксиомы и доказанное следствие нельзя применять к деформируемым телам, в частности, перенос точки приложения силы вдоль линии ее действия меняет напряженно-деформированное состояние тела.
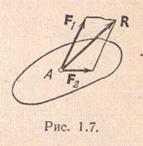 Аксиома 3. Не меняя состояния тела, две силы, приложенные к одной его точке, можно заменить одной равнодействующей силой, приложенной в одной и той же точке и равной их геометрической сумме (аксиома параллелограмма сил).
Аксиома 3. Не меняя состояния тела, две силы, приложенные к одной его точке, можно заменить одной равнодействующей силой, приложенной в одной и той же точке и равной их геометрической сумме (аксиома параллелограмма сил).
Эта аксиома устанавливает два обстоятельства:
первое – две силы F1 и F2, приложенные к одной точке, имеют одну равнодействующую, т.е. эквивалентны одной силе
(F1, F2) = R;
второе – аксиома полностью определяет модуль, точку приложения и направление равнодействующей силы
R = F1+F2.
Другими словами, равнодействующую R можно построить как диагональ параллелограмма со сторонами, совпадающими с F1 и F2.
Отметим, что третья аксиома применима к любым, не обязательно абсолютно твердым телам.
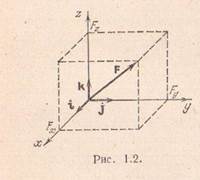
 Вторая и третья аксиомы статики дают возможность переходить от одной системы сил к другой системе, ей эквивалентной. В частности, они позволяют разложить любую силу Rна две, три и т.д. составляющие, т.е. перейти к другой системе сил, для которой сила Rявляется равнодействующей. Задавая, например два направления, которые лежат с Rв одной плоскости, можно построить параллелограмм, у которого диагональ изображает силу R. Тогда силы, направленные по сторонам параллелограмма, составят систему, для которой R будет равнодействующей. Аналогичное построение можно провести и в пространстве. Для этого достаточно из точки приложения силы R провести три прямые, не лежащие в одной плоскости, и построить на них параллелепипед с диагональю, изображающей силу R, и с ребрами, направленными по этим прямым.
Вторая и третья аксиомы статики дают возможность переходить от одной системы сил к другой системе, ей эквивалентной. В частности, они позволяют разложить любую силу Rна две, три и т.д. составляющие, т.е. перейти к другой системе сил, для которой сила Rявляется равнодействующей. Задавая, например два направления, которые лежат с Rв одной плоскости, можно построить параллелограмм, у которого диагональ изображает силу R. Тогда силы, направленные по сторонам параллелограмма, составят систему, для которой R будет равнодействующей. Аналогичное построение можно провести и в пространстве. Для этого достаточно из точки приложения силы R провести три прямые, не лежащие в одной плоскости, и построить на них параллелепипед с диагональю, изображающей силу R, и с ребрами, направленными по этим прямым.
Аксиома 4 (3-й закон Ньютона). Силы взаимодействия двух тел равны по модулю и направлены по одной прямой в противоположные стороны.
 Заметим, что силы взаимодействия двух тел не составляют систему уравновешенных сил, так как они приложены к разным телам.
Заметим, что силы взаимодействия двух тел не составляют систему уравновешенных сил, так как они приложены к разным телам.

 Если обозначить через Fсилу, с которой Солнце притягивает Землю, то Земля притягивает Солнце с такой же по модулю, но противоположно направленной силой –F.
Если обозначить через Fсилу, с которой Солнце притягивает Землю, то Земля притягивает Солнце с такой же по модулю, но противоположно направленной силой –F.
При движении тела по плоскости к нему будет приложена сила трения Т, направленная в сторону, противоположную движению. Это – сила, с которой неподвижная плоскость действует на тело. На основании аксиомы 4 тело действует на плоскость с такой же силой, но ее направление будет противоположно силе Т.
Аксиома 5. Равновесие деформируемого тела не нарушается, если жестко связать его точки и считать тело абсолютно твердым.
Этой аксиомой (ее иногда называют принципом отвердевания) пользуются в тех случаях, когда речь идет о равновесии тел, которые нельзя считать твердыми. Приложенные к таким телам внешние силы должны удовлетворять условиям равновесия твердого тела, однако для нетвердых тел эти условия являются лишь необходимыми, но не достаточными. Поясним это положение простым примером. Для равновесия абсолютно твердого невесомого стержня необходимо и достаточно, чтобы приложенные к концам стержня силы FиF' действовали по прямой, соединяющей его концы, были равны по модулю и направлены в разные стороны. Эти же условия необходимы и для равновесия отрезка невесомой нити, но для нити они недостаточны – необходимо дополнительно потребовать, чтобы силы, действующие на нить, были растягивающими, в то время как для стержня они могут быть и сжимающими.
В заключение рассмотрим случай эквивалентности нулю трех непараллельных сил, приложенных к твердому телу.
Теорема о трех непараллельных силах. Если под действием трех сил тело находится в равновесии и линии действия двух сил пересекаются, то все силы лежат в одной плоскости и их линии действия пересекаются в одной точке.
Пусть на тело действует система трех сил F1, F2иF3,причем линии действия сил F1иF2пересекаются в точке А. Согласно следствию из аксиомы 2 силы F1иF2можно перенести в точку А, а по аксиоме 3 их можно заменить одной силой R, причем
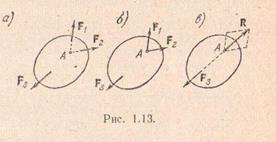 R = F1+F2.
R = F1+F2.
Таким образом,
рассматриваемая система сил приведена к двум силам RиF3. По условиям теоремы тело находится в равновесии, следовательно, по аксиоме 1 силы RиF3должны иметь общую линию действия, но тогда линии действия всех трех сил должны пересекаться в одной точке.
|
из
5.00
|
Обсуждение в статье: Сила. Система сил. Равновесие абсолютно твердого тела |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

