Работа и мощность тока

 

Основные формулы

 

1. Работа электрических сил по переносу заряда q на однородном участке цепи

dA = q· U = IU·dt.

2. Закон Джоуля – Ленца в интегральной форме:

dQ = I² Rdt ; dQ = .

3. Закон Джоуля – Ленца в дифференциальной форме:

ω = σ Е²,

где ω – удельная тепловая мощность тока в данной точке проводника, σ – проводимость, Е - напряженность электрического поля в проводнике.

4. Работа, совершаемая источником электрической энергии за время t:

A = ,

где ε – ЭДС источника, R_полн – полное сопротивление цепи.

5. Электрическая мощность, отдаваемая источником во внешнюю цепь (так называемая полезная мощность):

P = U·I = I²R или P_пол = ,

где r – внутреннее сопротивление источника, R - внешнее сопротивление цепи.

6. Полная мощность всей цепи

P₀ = I²R + I²r = I·ε или P_затр = .

 

 

7. Коэффициент полезного действия источника тока

η = ; η = ; η = .

Примеры решения задач

 

Задача 1. Определить работу электрических сил и количество теплоты, выделяемое ежесекундно: 1) в резисторе, по которому идет ток силой 1 А (разность потенциалов между концами резистора 2 В); 2) в аккумуляторе, который заряжается током силой 1 А (Разность потенциалов на его зажимах 2 В), ЭДС аккумулятора 1,3 В; 3) в батарее аккумуляторов, которая дает ток силой 1А на внешнюю нагрузку, разность потенциалов на зажимах батарей 2 В. ЭДС 2,6 В.

Дано: 1) I = 1А; φа- φв = 2В. 2) I = 1А; φа- φв = 2В ε = 1,3 В. 3) I = 1А; φа- φв = 2В ε = 2,6 В   А - ? Q - ?

Решение Рис. 4.1

1. Так как рассматриваемый участок не содержит ЭДС, то он является однородным. По закону Ома для такого участка цепи имеем φ_а- φ_в = IR. Значит, вся работа электрических сил идет на нагревание резистора.

A = Q = (φ_а- φ_в) I·t = 2·1·1 = 2 Дж.

2. При зарядке аккумулятора его зажимы присоединяют к источнику, разность потенциалов на полюсах которого постоянна. При этом ток внутри аккумулятора идет от положительного полюса к отрицательному (рис. 4.1), т.е. в направлении, обратном току разряда. Работу электрических сил снова вычислим по формуле

A = Q = (φ_а- φ_в) I·t = 3 Дж.

Чтобы определить количество выделенной теплоты, найдем сопротивление R участка А ε В. Поскольку он содержит источник тока, то участок является неоднородным. Применим закон Ома для неоднородного участка с учетом правила знаков.

I = , R = .

Подставив значение R в закон Джоуля – Ленца, получим

Q = I² R t = I² = (φ_а- φ_в - ε) It = 0,7 Дж.

В данном случае лишь часть работы электрических сил идет на нагревание аккумулятора, остальная же часть A – Q = 1,3 Дж превращается в химическую энергию заряжаемого аккумулятора.

 

3.Работу электрических сил также найдем по формуле

А =(φ_а- φ_в) It.

При этом обратим внимание на отличие данного случая от предыдущего. Если положительный знак разности φ_а- φ_в сохранился, то направление тока на участке

А ε В изменилось на противоположное (рис. 4.2), следовательно:

А =(φ_а- φ_в) (- I) t = - (φ_а- φ_в) It = 2 Дж.

	Рис . 4.2

 

Отрицательный знак ответа выражает то обстоятельство, что положительные заряды движутся внутри каждого аккумулятора от его низшего потенциала к высшему, т.е. против электрических сил. При этом положительную работу совершают сторонние (рис. 4.2) силы, перемещая заряды внутри аккумуляторов.

Найдем количество теплоты, выделенное в батарее. При этом сопротивление батареи r можно вычислить по закону Ома для неоднородного участка цепи А ε В. Теперь, учитывая направление тока и ЭДС, запишем

-I = .

Сопротивление батареи r можно найти как разность потенциалов между сопротивлением всей цепи и сопротивлением внешнего участка цепи:

r = R_полн – R = .

Подставив найденное значение r, получим

Q = I² r t = [ε – (φ_а- φ_в)]·I·t = 0,6 Дж.

Этот вариант задачи можно решать по-другому. Найдем работу электрических сил на внешнем участке цепи A-R-B:

А_внеш =(φ_а- φ_в) It = 2 Дж.

Однако работа электрических, т.е. кулоновских (но не сторонних), сил по перемещению зарядов по замкнутому пути всегда равна нулю. Значит,

А_внутр+А_внеш = 0.

Отсюда А_внутр= - А_внеш= - 2 Дж, что совпадает с решением второй части задачи.

Вся энергия, расходуемая батареей, превращается (посредством работы электрических сил) в тепло Q_общ, выделяющееся во всей цепи:

А_{батареи}= Q_общ= ε I t = 2,6 Дж.

Так как на внешнем участке выделяется количество теплоты

Q_внеш = А_внеш =2 Дж, то для батареи Q = Q_общ- Q_внеш = 0,6 Дж.

 

Задача 2. ЭДС батареи 12 В. Наибольшая сила тока, которую может дать батарея, равна 5 А. Какая наибольшая мощность может выделиться на подключенном к батарее резисторе с переменным сопротивлением?

 

Дано: Ε = 12 В Imax = 5 А Pmax - ?

Решение Полезная мощность выделяемая в резисторе, определяется формулой P = I2 R. (1) По закону Ома I = . (2)

 

Подставим выражение (2) в формулу (1).

P = ,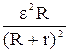

где R, r – сопротивление внешнего и внутреннего участка цепи соответственно. Отсюда видно, что при постоянных величинах ε, r мощность Р является функцией одной переменной – внешнего сопротивления R. Известно, что эта функция дает максимум при условии R= r. Следовательно,

P_max = .

Таким образом, задача сводится к отысканию сопротивлений r внутреннего участка цепи (батареи). Если учесть, что согласно закону Ома для замкнутой цепи наибольшая сила тока I_max будет при внешнем сопротивлении R=0 (ток короткого замыкания), то

I_max= или r = .

Отсюда P_max = .

Подставим числовые значения:

P_max = Вт.

Задача 3. Элемент замыкают сначала на внешнее сопротивление 2 Ом, а затем на внешнее сопротивление 0,5 Ом. Найти ЭДС элемента ε и его внутреннее сопротивление r, если известно, что в каждом из этих случаев мощность, выделяющаяся во внешней цепи, одинакова и равна 2,54 Вт.

 

Дано: R1 = 2 Ом R2 = 0,5 Ом Р1 = Р2 = Р Р = 2,54 Вт Ε-? r - ?

Решение Согласно закону Ома для полной цепи сила тока I = . Тогда мощность, выделяющаяся во внешней цепи: .

 

По условию задачи P₁= , (1)

. (2)

Получили систему из двух уравнений с двумя неизвестными ε и r.

Приравнивая эти уравнения, поскольку Р₁ = Р_2, тогда

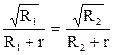
или

,

или

Тогда .

Подставляя числовые значения, получим

1 Ом.

Зная внутреннее сопротивление, найдем ε из уравнения (1) системы уравнений:

;

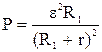ε = .

Подставим числовые значения:

В.

 

Задача 4. От батареи с ЭДС 500 В требуется передать энергию на расстояние 2,5 км. Потребляемая мощность 10 кВт. Найти минимальные потери мощности в сети, если диаметр медных проводов 1,5 см. Удельное сопротивление меди 1,7·10 ^-8 Ом·м.

Дано: Ε = 500 В Р =10 кВт =104 Вт l = 2,5 км =2,5·103 м d =1,5 см =1,5·10-2 м ρ =1,7·10 -8 Ом·м -?

Решение Ток передается по двухпроводной линии к потребителю (рис.4.3). Потеря мощности происходит в подводящих проводах. Рис. 4.3

Тогда = I² ∙R, где I = - сила тока в проводах, а R – сопротивление проводов.

R = ,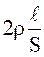

где ρ- удельное сопротивление, 2l – длина двухпроводной линии электропередачи, S = π d²/4 –площадь сечения проводов, диаметр которых d.

Тогда .

Подставляя числовые значения, получим

≈ 193 Вт.