 |
Главная |
Силы магнитного поля. Работа сил магнитного поля
|
из
5.00
|
Основные формулы
1. Сила Ампера, действующая на элемент тока d  в магнитном поле с индукцией В:
в магнитном поле с индукцией В:
dFA = I d  B sin
B sin 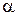 ,
,
где I-сила тока, 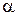 - угол между направлением вектора
- угол между направлением вектора  и силы тока.
и силы тока.
2. Сила Ампера, действующая на все элементы тока сложной формы проводника:

3. Сила Лоренца, действующая на заряд q, движущийся со скоростью V в магнитном поле с индукцией B:
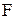 Л = q V B sin
Л = q V B sin 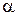 ,
,
где 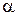 - угол между направлениями векторов
- угол между направлениями векторов 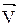 и
и 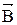 .
.
4. Сила взаимодействия параллельных проводников с токами I1 и I2
F = 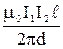 ,
,
где  - длина проводников, d - расстояние между ними,
- длина проводников, d - расстояние между ними, 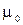 = 4
= 4 
 Н/А2 – магнитная постоянная вакуума.
Н/А2 – магнитная постоянная вакуума.
5. Сила, действующая на рамку с током в неоднородном магнитном поле:
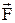 =
= 
 ,
,
где Рm – магнитный момент рамки с током, d  /d
/d 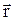 - градиент индукции магнитного поля.
- градиент индукции магнитного поля.
6. Работа магнитных сил по перемещению проводника с током
A = I 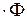 .
.
7. Работа магнитных сил по перемещению замкнутого контура c током
A = I (Ф2 –Ф1),
где Ф1 и Ф2 - магнитный поток через площадь, ограниченную контуром с током в начальном и конечном состояниях.
Примеры решения задач
Задача 1. Квадратная рамка с током 2 А расположена в одной плоскости с длинным прямым проводником, по которому течёт ток 10 А. Сторона рамки 15 см. Ближайшая сторона рамки отстоит от проводника на расстоянии 10 см. Найти силу, действующую на рамку.
 Дано:
I1 = 2 A
I2 = 10 A
a = 5 см = 0,15 м
в = 10 см = 0,1 м Дано:
I1 = 2 A
I2 = 10 A
a = 5 см = 0,15 м
в = 10 см = 0,1 м
 F-?
F-?
| Решение
Прямой проводник с током I1 создаёт вокруг себя неоднородное магнитное поле, индукция которого уменьшается с увеличением расстояния r согласно формуле
В1 = 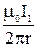 . (1) . (1)
|
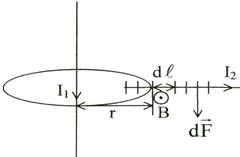
В таком магнитном поле на каждую сторону квадратной рамки с током I2 будет действовать сила Ампера, направление которой определяется по правилу левой руки (рис. 6.1).

|
|
Силы F1 и F3 можно найти, используя закон взаимодействия параллельных токов:
F1 = 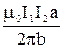 ,
,
F3 =  .
.
Для нахождения силы F2 разобьём проводник на элементы тока I2d  (рис. 6.2). Пусть некоторый элемент расположен на расстоянии r от тока I1. В месте расположения элемента тока I2d
(рис. 6.2). Пусть некоторый элемент расположен на расстоянии r от тока I1. В месте расположения элемента тока I2d  индукция поля
индукция поля  направлена к нам и определяется формулой (1). Сила Ампера, действующая на элемент тока I2d
направлена к нам и определяется формулой (1). Сила Ампера, действующая на элемент тока I2d  (d
(d  = dr):
= dr):
|
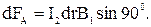
Поскольку все силы d 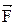 A направлены в одну сторону, то вся сила
A направлены в одну сторону, то вся сила
|
 .
.
Заметим, что сила F4 = F2 , но противоположно направлена.
Результирующая сила, действующая на рамку с током I2 :
F = F1 - F3 + F2 - F4 = F1 - F3 .
F = 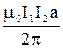
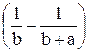 =
= 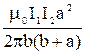 .
.
Подставим числовые значения:
F =  = 0,36
= 0,36  .
.
Задача 2. Проводник в виде тонкого полукольца радиусом 0,1 м находится в однородном магнитном поле с индукцией 0,05 Тл. По проводнику течёт ток 10 А. Найти силу, действующую на проводник, если плоскость полукольца перпендикулярна линиям индукции.
 |
Дано:
R = 0,1 м
В = 5×102 Тл
I = 10 А
 F - ?
F - ?
| Решение
Разобьем проводник на элементы тока Id  , причем d , причем d  = R×da
(рис. 6.3). = R×da
(рис. 6.3).
 Рис. 6.3
Рис. 6.3
|
Положение элемента на окружности будем углом 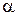 . Со стороны магнитного поля на элемент тока будет действовать сила Ампера dF:
. Со стороны магнитного поля на элемент тока будет действовать сила Ампера dF:
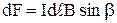 , (1)
, (1)
где угол между элементом тока и магнитной индукцией  .
.
Разложим силу dF на две составляющие силы dFY и dFX.
 ,
, 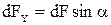 .
.
Заметим, что ввиду симметрии силы dFXi от всех элементов проводника уничтожат друг друга, а результирующая сила по оси Y будет отлична от нуля.
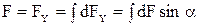 . (2)
. (2)
Подставим в выражение (2) формулу (1) и после интегрирования получим
 =
= 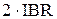 .
.
Подставим числовые значения:
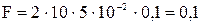 Н.
Н.
Задача 3. Небольшая катушка с током, имеющая магнитный момент 2 А/м2, находится на оси кругового витка радиусом 20 см, по которому идёт ток 10 А. Найти модуль силы, действующей на катушку, если её расстояние от центра витка равно 10 см. Вектор магнитного момента совпадает по направлению с осью витка.
Дано:
Рм = 2 А/ м2
R = 20 см=0,2 м
I = 10 А
А=10 см=0,1 м
 F - ?
F - ?
|
Магнитное поле кругового витка является неоднородным. В таком поле на магнитный момент катушки будет действовать сила
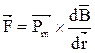 (1) (1)
Градиент индукции |
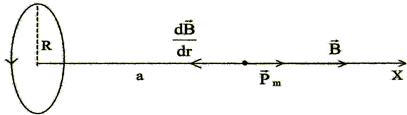
| |
Выберем ось X вдоль оси витка и спроецируем выражение (1) на эту ось.
 . (2)
. (2)
Индукция магнитного поля от кругового тока
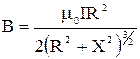 . (3)
. (3)
Возьмём производную от выражения (3) по переменной X:
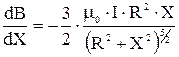 .
.
Окончательно для силы FX имеем при X = а
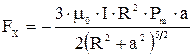 .
.
Знак минус означает, что катушка будет втягиваться в область сильного поля.
Подставим числовые значения:
 =
= 
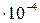 Н =
Н =  мН.
мН.
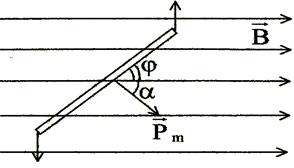
Задача 4. Квадратная рамка со стороной 2 см, содержащая 100 витков, подвешена на упругой нити с постоянной кручения 10 мкН/град. Плоскость рамки совпадает с направлением линий индукции внешнего магнитного поля. Определить индукцию магнитного поля, если при пропускании по рамке тока 1 А она повернулась на угол 600, а также определить работу сил, действующих со стороны магнитного поля (рис. 6.5).
 Дано: Решение
Дано: Решение
 а = 2 см = 2
а = 2 см = 2 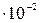 м
м
N = 100 витков
C = 10-5 Н/град
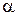 = 900
= 900
| |
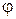 = 600
= 600

B-? А-?
Рис. 6.5
Рамка с током находится в равновесии при выполнении условия:  , где
, где  -момент сил, действующих на рамку с током,
-момент сил, действующих на рамку с током,  - момент упругих сил, действующих на рамку.
- момент упругих сил, действующих на рамку.
Известно, что
 M1 =
M1 = 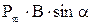 ,
,
M2 = 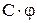 ,
, 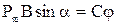 .
.
Магнитный момент рамки  .
.
Учитывая, что 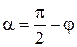 , получим
, получим 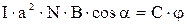 .
.
Теперь можно найти величину индукции магнитного поля:
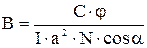 .
.
| |
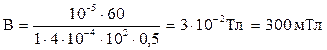 .
.
Найдём работу сил магнитного поля по повороту рамки на угол  :
:
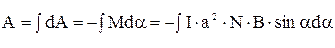 ,
,
 .
.
Знак минус в выражении для 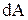 означает, что под действием момента сил М происходит убыль угла α.
означает, что под действием момента сил М происходит убыль угла α.
Работу сил магнитного поля можно вычислить и другим способом:
 ,
,
где  - приращение потока вектора
- приращение потока вектора  через поверхность контура с током I.
через поверхность контура с током I.
|
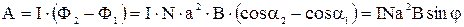 .
.
Задача 5. Протон движется в магнитном поле с индукцией  Тл по винтовой линии радиусом 2 см и шагом 5 см. Определить скорость протона и угол её наклона к линиям индукции.
Тл по винтовой линии радиусом 2 см и шагом 5 см. Определить скорость протона и угол её наклона к линиям индукции.
Дано:
R = 2×10-2 м
В = 10-2 Тл
qп = 1,.6×10-19 Кл
mп = 1,67×10-27 кг
h = 5 см = 5×10-2 м
 V - ? a - ?
V - ? a - ?
|  Решение
Решение
 Заряженная частица движется в магнитном поле по винтовой линии, если она в него влетает под углом a к линиям индукции (рис 6.6). Заряженная частица движется в магнитном поле по винтовой линии, если она в него влетает под углом a к линиям индукции (рис 6.6).
|
| |
| |
| |
| |
| |
Движение по винтовой линии считается двумерным. Введём оси координат X и Y . Поскольку магнитное поле однородное, то движение вдоль общих осей будет равномерным. Скорость частицы  раскладываем на две проекции VX и VY, причём
раскладываем на две проекции VX и VY, причём
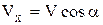 , (1)
, (1)
 . (2)
. (2)
Шаг винтовой линии (расстояние между витками) определяется как
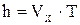 , (3)
, (3)
где Т – период обращения по окружности, которая расположена в плоскости Y. Движение по окружности происходит со скоростью  . Период обращения
. Период обращения
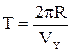 . (4)
. (4)
Выражение (4) подставим в формулу (3):
 .
.
Из последнего выражения определим угол наклона скорости V к оси X:
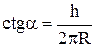 .
.
 ,
,  .
.
Радиус винтовой линии определяется выражением
 ,
,
из которого определим скорость VY:
 .
.
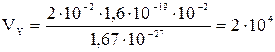 м/с.
м/с.
Искомую скорость V определим по формуле (2):
 м/с.
м/с.
Задача 6. Квадратная рамка с током 5 А расположена в одной плоскости с длинным проводником, по которому течёт ток 15 А. Сторона рамки 50 см. Ближайшая сторона рамки расположена на расстоянии 10 см от длинного проводника. Найти работу, которую нужно совершить для поворота рамки на угол 900, если силу тока поддерживать неизменной.
|
 Дано:
Дано:
I1 = 5 A
I2 = 15 A
a = 50 см = 0,5 м
в = 10 см = 0,1 м

 |
Так как магнитное поле проводника с током I2 неоднородное, сначала определим элементарный поток dФ через площадку dS = 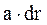 , в пределах которой индукцию магнитного поля можно считать постоянной величиной (рис. 6.7):
, в пределах которой индукцию магнитного поля можно считать постоянной величиной (рис. 6.7):
 ,
,
где 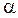 - угол между нормалью к элементу dS и вектором индукции
- угол между нормалью к элементу dS и вектором индукции 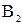 =
= 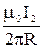 .
.
Полный магнитный поток через площадь всей рамки найдём суммированием всех dФ:
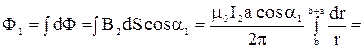
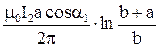 .
.
| |

|
Соответственно после поворота магнитный поток 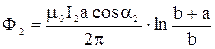 .
.
Так как 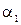 = 0,
= 0,  , то Ф2 = 0. Окончательно работа по повороту рамки
, то Ф2 = 0. Окончательно работа по повороту рамки
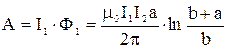 .
.
Подставим числовые значения:
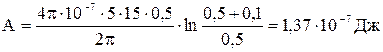 .
.
|
из
5.00
|
Обсуждение в статье: Силы магнитного поля. Работа сил магнитного поля |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы


 Решение
Решение направлен в сторону возрастания индукции (рис 6.4), направление магнитной индукции В определяется по правилу буравчика.
направлен в сторону возрастания индукции (рис 6.4), направление магнитной индукции В определяется по правилу буравчика.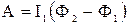 , (1)
где Ф1 и Ф2 – магнитные потоки, пронизывающие рамку в начальном и конечном состояниях.
, (1)
где Ф1 и Ф2 – магнитные потоки, пронизывающие рамку в начальном и конечном состояниях.