 |
Главная |
Методы расчёта магнитных полей
|
из
5.00
|
Основные формулы
1. Магнитный момент рамки с током
 .
.
2. Вращающий момент, действующий на рамку с током:
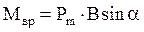 .
.
3. Вектор индукции  и вектор напряжённости
и вектор напряжённости  магнитного поля и их циркуляции по замкнутому контуру:
магнитного поля и их циркуляции по замкнутому контуру:
|
 ,
,  ,
,
|
 ,
,  ,
, 

 ,
,
где  - магнитная постоянная вакуума,
- магнитная постоянная вакуума,  H/A2;
H/A2;  - магнитная проницаемость вещества,
- магнитная проницаемость вещества,  - алгебраическая сумма токов, охватываемых замкнутым контуром,
- алгебраическая сумма токов, охватываемых замкнутым контуром,  - намагниченность вещества.
- намагниченность вещества.
4. Поток вектора  через замкнутую поверхность
через замкнутую поверхность
 .
.
5. Некоторые соотношения для магнетиков:
 ,
,
 ,
,
где 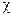 - восприимчивость вещества.
- восприимчивость вещества.
6. Граничные условия для векторов  и
и  :
:
 ,
,  ,
,
 ,
,  ,
,  ,
,
где  - нормальная составляющая вектора
- нормальная составляющая вектора  ,
,  - тангенциальная составляющая вектора
- тангенциальная составляющая вектора  ,
,  - углы между векторами
- углы между векторами  и перпендикуляром к поверхности границы раздела в разных средах.
и перпендикуляром к поверхности границы раздела в разных средах.
7. Принцип суперпозиции для векторов 
 ,
,
где  - индукция от полей, созданных различными источниками.
- индукция от полей, созданных различными источниками.
 ,
,
если источники магнитных полей расположены непрерывно .
8. Индукция магнитного поля движущегося заряда
 .
.
9. Индукция магнитного поля элемента тока (закон Био-Савара-Лапласа)
 .
.
10. Индукция магнитного поля прямолинейного проводника с током бесконечной и конечной длины соответственно
 ,
,  .
.
11. Индукция магнитного поля в центре и на оси кругового тока соответственно
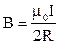 ,
,  .
.
12. Индукция магнитного поля внутри соленоида и тороида соответственно
 ,
,  ,
,
где N - общее число витков,  - длина. Длина тороида
- длина. Длина тороида  , где
, где  - радиус средней линии тороида.
- радиус средней линии тороида.
Примеры решения задач
Задача 1. Бесконечно длинный проводник с током 5 А делает петлю, лежащую в перпендикулярной току плоскости. Найти напряженность магнитного поля в центре петли, если её радиус 0,5 м.

|
I = 5 A
R = 0,5м
 |
H - ?

Направление вектора индукции магнитного поля в обоих случаях определяем по правилу буравчика: от бесконечно длинного тока вектор В1 направлен к нам, а от кругового тока вектор В2направлен справа налево по оси кругового тока
(рис. 5.1а). В1 и В2 перпендикулярны друг к другу. Результирующий вектор Внаправлен по диагонали параллелограмма, построенного на векторах В1 и В2
(рис. 5.1б). Числовое значение В находим по теореме Пифагора
 , (1)
, (1)
причём величины  и
и  находим по соответствующим формулам:
находим по соответствующим формулам:
 ,
,  . (2)
. (2)
В вакууме напряжённость Н и индукция В связаны соотношением
 . (3)
. (3)
Подставляя (3) и (2) в (1), для напряжённости получим формулу
| |
 .
. 
Подставим числовые значения:
 A/м.
A/м.
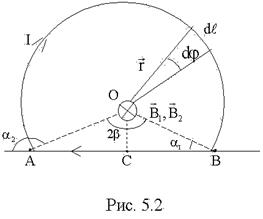
Задача 2. Ток 5 А течёт по тонкому изогнутому проводнику (рис. 5.2). Радиус изогнутой части проводника R = 12 см, угол  . Найти индукцию магнитного поля в точке O.
. Найти индукцию магнитного поля в точке O.
  Дано: I = 5 A
R = 12 см = 0,12 м Дано: I = 5 A
R = 12 см = 0,12 м
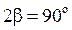 
 В - ?
В - ?
|  Решение Решение
|
Индукция  магнитного поля в точке О является векторной суммой индукций В1 и В2, создаваемых током, протекающим по круговому и прямолинейному участкам проводника. Все элементы тока создают в точке О магнитные поля, векторы индукции которых направлены в одну сторону (перпендикулярно плоскости (рис. 5.2), “от нас”). Поэтому от векторной суммы можно перейти к алгебраической, т.е.
магнитного поля в точке О является векторной суммой индукций В1 и В2, создаваемых током, протекающим по круговому и прямолинейному участкам проводника. Все элементы тока создают в точке О магнитные поля, векторы индукции которых направлены в одну сторону (перпендикулярно плоскости (рис. 5.2), “от нас”). Поэтому от векторной суммы можно перейти к алгебраической, т.е.
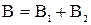 .
.
Вычислим индукцию  , создаваемую участком кругового тока, используя закон Био-Савара-Лапласа :
, создаваемую участком кругового тока, используя закон Био-Савара-Лапласа :

 .
.
Для всех участков кругового тока угол между  и
и  равен
равен  , а элемент длины
, а элемент длины 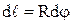 . Угол
. Угол  при интегрировании по участку кругового тока изменяется от 0 до
при интегрировании по участку кругового тока изменяется от 0 до  . Вычисление интеграла даёт следующее выражение:
. Вычисление интеграла даёт следующее выражение:
 .
.
Для вычисления индукции  , создаваемой прямолинейным участком тока BCA, можно воспользоваться выражением, определяющим индукцию магнитного поля прямого тока:
, создаваемой прямолинейным участком тока BCA, можно воспользоваться выражением, определяющим индукцию магнитного поля прямого тока:
 .
.
Для данной задачи  ;
; 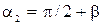 ;
; 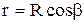 (из треугольников AOC и COB) . Подстановка значений даёт
(из треугольников AOC и COB) . Подстановка значений даёт
 .
.
Учитывая, что  , для величины B окончательно получим
, для величины B окончательно получим
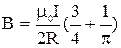 .
.
Подставим числовые значения:
 мкКл.
мкКл.
Задача 3. Тонкий непроводящий диск радиусом R, равномерно заряженный с поверхностной плотностью  , вращается вокруг своей оси с угловой скоростью
, вращается вокруг своей оси с угловой скоростью  . Найти: а) индукцию магнитного поля в центре диска; б) магнитный момент диска. (рис. 5.3).
. Найти: а) индукцию магнитного поля в центре диска; б) магнитный момент диска. (рис. 5.3).
 | |||
 | |||
|
R
s

 | |||
| |


Круговой ток создаёт в центре диска магнитное поле с индукцией dB. Используя принцип суперпозиции и учитывая, что все элементарные кольцевые токи dI создают в центре диска магнитные поля одного направления, получим

 .
.
 .
.
Магнитный момент тока dI
 .
.
 .
.
Задача 4. По круглому однородному прямому проводу радиусом 2 см течёт постоянный ток плотностью j = 10А/м. Найти индукцию магнитного поля в точках, лежащих внутри и вне соленоида на расстояниях 1 и 5 см соответственно. Построить график B(r).
Дано:  R = 2
R = 2 
 A/м A/м
 см см 
 см см 
 В1 -? В2 - ?
В1 -? В2 - ?
| Решение
Величина индукции зависит только от расстояния до оси провода (рис. 5.4). Вектор  направлен к силовой линии, которая представляет собой окружность с центром на оси провода. Для вычисления магнитной индукции используем теорему о циркуляции: циркуляция вектора индукции магнитного поля по замкнутому контуру равна алгебраической сумме токов, охваченных этим контуром, умноженным на величину направлен к силовой линии, которая представляет собой окружность с центром на оси провода. Для вычисления магнитной индукции используем теорему о циркуляции: циркуляция вектора индукции магнитного поля по замкнутому контуру равна алгебраической сумме токов, охваченных этим контуром, умноженным на величину  : :  . .
|
 Рис. 5.4
Рис. 5.4
Рассмотрим область точек, лежащих внутри провода  . В качестве контура интегрирования выберем окружность радиусом r. Направление обхода и направление вектора j свяжем правилом буравчика. По теореме о циркуляции вектора В
. В качестве контура интегрирования выберем окружность радиусом r. Направление обхода и направление вектора j свяжем правилом буравчика. По теореме о циркуляции вектора В
 .
.
 (1)
(1)
Для точек, лежащих вне провода  , решение задачи аналогично предыдущему случаю. Контур интегрирования теперь охватывает площадь сечения проводника, поэтому сила тока
, решение задачи аналогично предыдущему случаю. Контур интегрирования теперь охватывает площадь сечения проводника, поэтому сила тока
 .
.
По теореме о циркуляции вектора В
 ,
,
 (2)
(2)
Произведём расчёт формул (1) и (2) .
 нТл,
нТл,
 нТл.
нТл.
 График зависимости магнитной индукции B от расстояния r представлен на рис. 5.5.
График зависимости магнитной индукции B от расстояния r представлен на рис. 5.5.
Рис. 5.5
Задача 5. Постоянный ток 10 А течёт по прямому проводнику круглого сечения длиной 50 см (рис. 5.6). Найти поток вектора магнитной индукции через одну из половин осевого сечения.
 Дано: Решение
Дано: Решение
 I = 10 А
I = 10 А
 см
см  м
м

Ф - ?
Рис. 5.6
Поток вектора индукции определяется интегралом
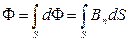 ,
,
где  - проекция вектора
- проекция вектора  на нормаль к площадке. В нашем случае
на нормаль к площадке. В нашем случае  , т.к. вектор
, т.к. вектор 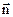 совпадает по направлению с вектором
совпадает по направлению с вектором 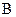 . Из решения предыдущей задачи для точек, лежащих внутри проводника, индукция зависит от расстояния.
. Из решения предыдущей задачи для точек, лежащих внутри проводника, индукция зависит от расстояния.
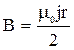 .
.
Выделим в сечении полоску шириной dr и длиной  , находящуюся на расстоянии r от оси провода. В пределах площадки dS
, находящуюся на расстоянии r от оси провода. В пределах площадки dS  величину индукции можно считать постоянной, тогда элементарный поток вектора магнитной индукции через неё
величину индукции можно считать постоянной, тогда элементарный поток вектора магнитной индукции через неё
 .
.
Полный поток магнитной индукции
 .
.
Учитывая, что 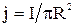 , получим
, получим
 .
.
Подставим числовые значения:
 нВб.
нВб.
Задача 6. Сколько ампер-витков необходимо для получения индукции величиной 1,4 Тл в электромагните с железным сердечником длиной 90 см и воздушным промежутком длиной 5 мм. Рассеянием магнитного потока в воздушном промежутке пренебречь (рис. 5.7).

 Дано: Решение
Дано: Решение
| |
 Тл
Тл
| |
 см
см 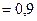 м
м 
 см
см 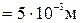

I∙N - ?
Исходя из граничных условий на границе раздела воздух-железо, в области воздушного зазора можно записать, что нормальные составляющие вектора магнитной индукции в двух средах не изменяются. Тогда
 .
.
Применим к данной задаче теорему о циркуляции для магнетика

или
 . (1)
. (1)
Величину напряжённости поля  в магнетике найдём по графику зависимости
в магнетике найдём по графику зависимости  , которая конкретна для каждого сорта железного магнетика. На рис. 5.8 представлена такая зависимость. При значении B = 1,4 Тл напряжённость
, которая конкретна для каждого сорта железного магнетика. На рис. 5.8 представлена такая зависимость. При значении B = 1,4 Тл напряжённость
H = 1700  .
.
 |
В воздушном зазоре величины B и H связаны соотношением  . Тогда из формулы (1) число ампер-витков
. Тогда из формулы (1) число ампер-витков
 .
.
Подставим числовые значения:


Задача 7. Квадратная рамка расположена в одной плоскости с длинным прямым проводником с током 10 А. Сторона рамки 1м. Ближайшая к проводнику сторона рамки расположена от него на расстоянии 0,5 м. Найти поток вектора  через площадь рамки.
через площадь рамки.

|

 м
м
 м
м

Ф - ?
Вектор  направлен по касательной к силовой линии, а направление тока I и направление силовой линии связаны правилом буравчика. На рис. 5.9 крестики означают, что вектор
направлен по касательной к силовой линии, а направление тока I и направление силовой линии связаны правилом буравчика. На рис. 5.9 крестики означают, что вектор  направлен от нас. Нормаль к поверхности S также направлена от нас.
направлен от нас. Нормаль к поверхности S также направлена от нас.
В пределах рамки магнитное поле неоднородное, поэтому плоскость рамки разделим на элементарные полоски площадью  Они настолько малы, что в пределах dS индукцию B можно считать постоянной величиной. Тогда воспользуемся формулой элементарного потока
Они настолько малы, что в пределах dS индукцию B можно считать постоянной величиной. Тогда воспользуемся формулой элементарного потока  :
:
 . (2)
. (2)
 Подставим в (2) формулу (1) и учтём, что угол
Подставим в (2) формулу (1) и учтём, что угол  .
.
Тогда
 .
.
Полный поток вектора  через поверхность S рамки равен алгебраической сумме элементарных потоков
через поверхность S рамки равен алгебраической сумме элементарных потоков  :
:
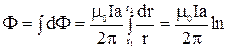

 .
.
Подставим числовые значения:
 мкВб.
мкВб.
|
из
5.00
|
Обсуждение в статье: Методы расчёта магнитных полей |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы



 . Вследствие вращения данный заряд создаёт электрический круговой ток силой
. Вследствие вращения данный заряд создаёт электрический круговой ток силой  .
.
 . (1)
. (1)