Глава 1. Ось и отрезок оси. Координаты на прямой

Д.В.Клетеник

"Сборник задач по аналитической геометрии". М., Наука, Физматлит, 1998.

Предисловие к первому изданию

Настоящий сборник задач соответствует курсу аналитической геометрии тех факультетов высших технических учебных заведений, где действуют нормальные программы по физико-математическим и общетехническим дисциплинам, и совершенно не содержит задач по разделам аналитической геометрии, не входящим в программу втузов. При составлении сборника автор обращал особое внимание на потребности теоретической механики, поскольку она является первым и непосредственным потребителем материала аналитической геометрии.

Использование этого сборника на факультетах экономического, химического и сельскохозяйственного профилей не исключается; однако ни в расположении, ни в подборе задач специфика этих факультетов не учитывалась.

По основным вопросам аналитической геометрии, входящим в программу втузов, дано задач несколько больше того, что обычно предлагается студентам на групповых занятиях и на дом. Тем самым при использовании сборника руководители практических занятий будут иметь возможность выбора материала, а домашние задания смогут давать в нескольких вариантах. Особенно значительный по объёму § 16 ("Окружность") включает комбинированные задачи на уравнения окружности и прямой, что дает возможность повторить один из наиболее важных разделов курса - уравнение прямой на плоскости.

После изучения теории линий второго порядка полезно давать студентам индивидуальное домашнее задание - на приведение общего уравнения второй степени к каноническому виду; в § 22 содержится достаточное количество аналогичных задач с различными числовыми данными.

Имея в виду студентов заочных институтов и лиц, изучающих высшую математику самостоятельно, автор в начале каждой главы даёт, кроме списка формул, также все основные определения и формулировки теорем.

Настоящий сборник задач составлен применительно к учебнику Н. В. Ефимова "Краткий курс аналитической геометрии"; при составлении сборника учитывались последовательность изложения материала в книге Н. В. Ефимова и употребляемая в ней символика.

Считаю своим долгом выразить благодарность коллективу кафедры высшей математики Московского лесотехнического института за помощь при составлении этого сборника и за критику первого варианта рукописи.

Д. Клетеник

Предисловие ко второму изданию

Для второго издания сборник задач переработан и дополнен. Наиболее существенной переработке подверглась первая часть задачника ("Аналитическая геометрия на плоскости"). Значительно изменён характер главы 1 ("Простейшие задачи аналитической геометрии на плоскости") и главы 3 ("Линии первого порядка"). Здесь изменения имеют принципиальный характер, поскольку во втором издании в первой части исключено понятие свободного вектора. Значительно переделана также глава 5 (в основном посвящённая общей теории линий второго порядка). Переработка этой главы направлена к тому, чтобы выдвинуть на первый план уравнения центральных кривых второго порядка (упрощение которых наиболее существенно для теоретической механики). Количество задач во всех разделах значительно увеличено (в первом издании задачник содержал 920 задач, в новом-1261). Увеличение объёма задачника произведено в значительной степени за счёт включения комбинированных и более сложных задач.

В новом издании задачник, сохраняя тесную связь с курсом аналитической геометрии Н. В. Ефимова (2-е издание), полностью приспособлен для использования с курсом И. И. Привалова. Считаю своим долгом выразить благодарность Н. Т. Хроленко за оказанную мне помощь при проверке ответов.

Д. Клетеник

Часть 1. Аналитическая геометрия на плоскости

Глава 1. Простейшие задачи аналитической геометрии на плоскости

Глава 1. Ось и отрезок оси. Координаты на прямой

		Построить точки А(3), В(5), С(-1), D(2/3), Е(-3/7), , .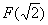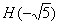
		Построить точки, координаты которых удовлетворяют уравнениям:
	2.1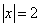
	2.2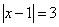
	2.3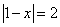
	2.4
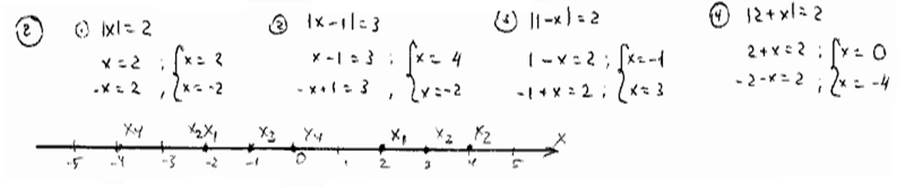
		Охарактеризовать геометрически расположение точек, координаты которых удовлетворяют неравенствам:
	3.1	x>2
	3.2	x – 3? 0
	3.3	12 – x <0
	3.4	2x – 3 ? 0
	3.5	3x – 5 >0
	3.6	1 < x < 3
	3.7	–2 < x < 3
	3.8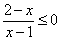
	3.9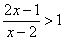
	3.10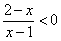
	3.11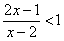
	3.12	x2 – 8x +15 ? 0
	3.13	x2 – 8x + 15 >0
	3.14	x2 + x – 12>0
	3.15	x2 + x -12? 0
		Определить величину АВ и длину отрезка, заданного точками:
	4.1	А(3) и В(11)
	4.2	А(5) и В(2)
	4.3	А(-1) и В(3)
	4.4	А(-5) и В(-3)
	4.5	А(-1) и В(-3)
	4.6	А(-7) и В(-5)
		Вычислить координату точки А, если известны:
	5.1	В(3) и АВ=5
	5.2	В(2) и АВ=-3
	5.3	В(-1) и ВА=2
	5.4	В(-5) и ВА=-3
	5.5	В(0) и =2
	5.6	В(2) и =3
	5.7	В(-1) и =5
	5.8	В(-5) и =2
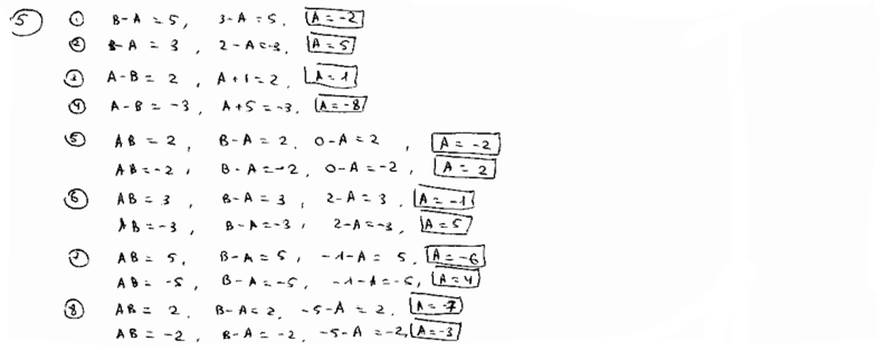
		Охарактеризовать геометрически расположение точек, координаты которых удовлетворяют следующим неравенствам:
	6.1
	6.2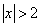
	6.3
	6.4
	6.5
	6.6
	6.7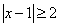
	6.8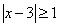
	6.9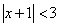
	6.10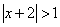
	6.11
	6.12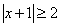
		Определить отношение l =AC/CB, в котором точка С делит отрезок АВ при следующих данных:
	7.1	А(2), В(6), С(4)
	7.2	А(2), В(4), С(7)
	7.3	А(-1), В(5), С(3)
	7.4	А(1), В(13), С(5)
	7.5	А(5), В(-2), С(-5)
		Даны три точки А(-7), В(-1), С(1). Определить отношение l , в котором каждая из них делит отрезок, ограниченный двумя другими.
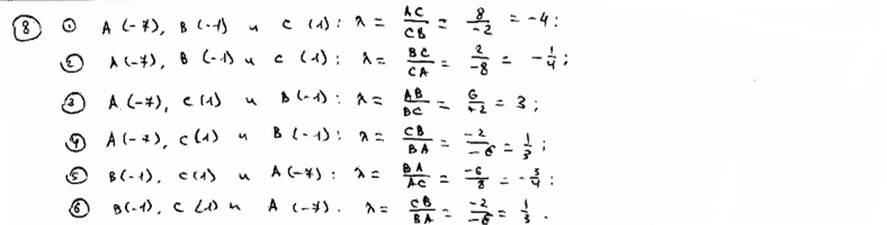
		Определить отношение l =М1М/ММ2, в котором данная точка М(х) делит отрезок М1М2, ограниченный точками М1(х1) и М2(х2).
		Определить координату х точки М, деляющей отрезок М1М2, ограниченный данными точками М1(х1) и М2(х2), в данном отношении l (l =М1М/ММ2).
		Определить координату х середины орезка, ограниченного данными точками М1(х1) и М2(х2).
		Определить координату х середины отрезка, ограниченного двумя данными точками, в каждом из следующих случаев:
	12.1	А(3) и В(5)
	12.2	С(-1) и D(5)
	12.3	M1(-1) и M2(-3)
	12.4	P1(-5) и P2(1)
	12.5	Q1(3) и Q2(-4)
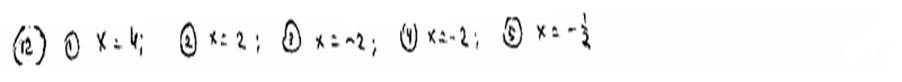
		Определить координату точки М, если известны:
	13.1	М1(3), М2(7) и l =М1М/ММ2=2
	13.2	А(2), В(-5) и l =АМ/МВ=3
	13.3	С(-1), D(3) и l =CM/MD=1/2
	13.4	А(-1), В(3) и l =АМ/МВ=-2
	13.5	А(1), В(-3) и l =ВМ/МА=-3
	13.6	А(-2), В(-1) и l =ВМ/МА=-1/2
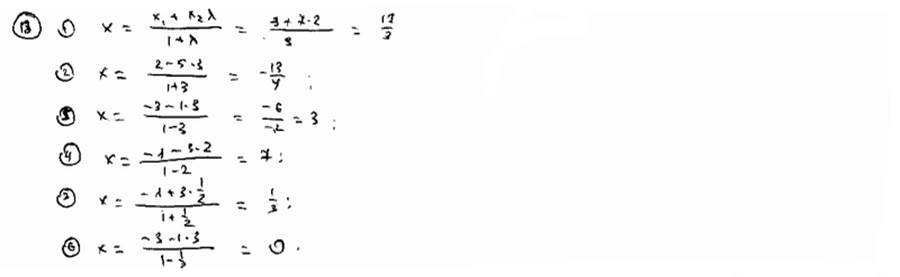
		Даны две точки А(5) и В(-3). Определить:
	14.1	координату точки M, симметричной точке А относительно точки В
	14.2	координату точки N, симметричной точке В относительно точки А
		Даны две точки А(5) и В(19), разделен на три равные части. Определить координаты точек деления.
		Определить координаты концов А и В отрезка, который точками P(-25) и Q(-9) разделен на три равные части.