 |
Главная |
Глава 31. Скалярное произведение векторов
|
из
5.00
|
| 795 | Векторы  и и 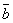 образуют угол образуют угол  , зная, что , зная, что  =3, =3,  =4, вычислить: =4, вычислить:
| |
| 795.1 | 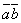 ; ;
| |
| 795.2 | 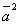 ; ;
| |
| 795.3 |  ; ;
| |
| 795.4 | 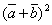 ; ;
| |
| 795.5 |  ; ;
| |
| 795.6 |  ; ;
| |
| 795.7 |  ; ;

| |
| 796 | Векторы  и и 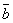 взаимно перпендикулярны; вектор взаимно перпендикулярны; вектор  образует с ними углы, равные образует с ними углы, равные  ; зная, что ; зная, что  =3, =3,  =5, =5,  =8, вычислить: =8, вычислить:
| |
| 796.1 | 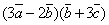 ; ;
| |
| 796.2 | 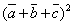 ; ;
| |
| 796.3 | 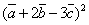 . .
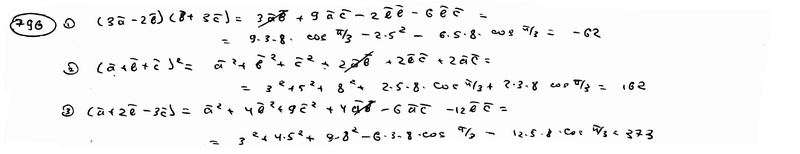
| |
| 797 | Доказать справедливость тождества  и выяснить его геометрический смысл. и выяснить его геометрический смысл.

| |
| 798 | Доказать, что  ; в каких случаях здесь может иметь место знак равенства? ; в каких случаях здесь может иметь место знак равенства?

| |
| 799 | Считая, что каждый из векторов  , , 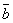 , ,  отличен от нуля, установить, при каком их взаимном расположении справедливо равенство отличен от нуля, установить, при каком их взаимном расположении справедливо равенство 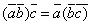 . .

| |
| 800 | Даны единичные вектторы  , , 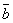 , ,  , удовлетворяющие условию , удовлетворяющие условию  . Вычислить . Вычислить  . .

| |
| 801 | Даны векторы  , , 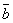 , ,  , удовлетворяющие условию , удовлетворяющие условию  . Зная, что . Зная, что  =3, =3,  =1, =1,  =4, вычислить =4, вычислить  . .

| |
| 802 | Векторы  , , 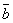 , ,  попарно образуют друг с другом углы, каждый из которых равен 600. Зная, что попарно образуют друг с другом углы, каждый из которых равен 600. Зная, что  =2, =2,  =2, =2,  =6, определить модуль вектора =6, определить модуль вектора  . .

| |
| 803 | Дано, что  =3, =3,  =5. Определить, при каком значении =5. Определить, при каком значении  векторы векторы  , ,  будут взаимно перпендикулярны. будут взаимно перпендикулярны.

| |
| 804 | Какому условию должны удовлетворять векторы  и и 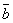 , чтобы вектор , чтобы вектор 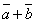 был перпендикулярен к вектору был перпендикулярен к вектору  . .

| |
| 805 | Доказать, что вектор  перпендикулярен к вектору перпендикулярен к вектору  . .

| |
| 806 | Доказать, что вектор  перпендикулярен к вектору перпендикулярен к вектору  . .

| |
| 807 | Даны векторы  и и 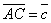 , совпадающие со сторонами треугольника АВС. Найти разложение вектора, приложенного к вершине В этого треугольника и совпадающего с его высотой BD по базису , совпадающие со сторонами треугольника АВС. Найти разложение вектора, приложенного к вершине В этого треугольника и совпадающего с его высотой BD по базису 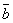 , ,  . .

| |
| 808 | Векторы  и и 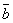 образуют угол образуют угол  ; зная, что ; зная, что  , , 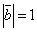 , вычислить угол , вычислить угол  между векторами между векторами  и и  . .

| |
| 809 | Вычислить тупой угол, образованный медианами, проведенными из вершин острых углов равноберденного прямоугольного треугольника.

| |
| 810 | Определить геометрическое место концов переменного вектора 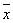 , если его начало находится в данной точке А и вектор , если его начало находится в данной точке А и вектор 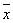 удовлетворяет условию удовлетворяет условию  , где , где  - данный вектор и - данный вектор и  - данное число. - данное число.
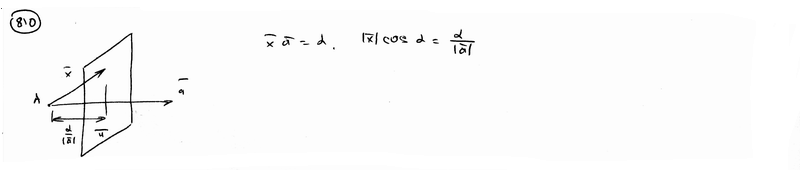
| |
| 811 | Определить геометрическое место концов переменного вектора 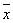 , если его начало находится в данной точке А и вектор , если его начало находится в данной точке А и вектор 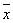 удовлетворяет условиям удовлетворяет условиям  , ,  , где , где  и и 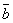 - данные неколлинеарные векторы и - данные неколлинеарные векторы и  , ,  - данные числа. - данные числа.

| |
| 812 | Даны векторы  ={4; -2; -4}, ={4; -2; -4}, 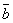 ={6; -3; 2}. Вычислить: ={6; -3; 2}. Вычислить:
| |
| 812.1 | 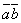 ; ;
| |
| 812.2 |  ; ;
| |
| 812.3 | 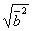 ; ;
| |
| 812.4 |  ; ;
| |
| 812.5 | 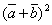 ; ;
| |
| 812.6 |  . .

| |
| 813 | Вычислить, какую работу произведет сила f={3; -5; 2}, когда ее точка приложения перемещается из начала в конец вектора  ={2; -5; -7}. ={2; -5; -7}.

| |
| 814 | Даны точки A(-1; 3; -7), B(2; -1; 5), C(0; 1; -5). Вычислить: | |
| 814.1 |  ; ;
| |
| 814.2 | 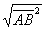 ; ;
| |
| 814.3 |  ; ;
| |
| 814.5 | Найти координаты векторов  и и  . .

| |
| 815 | Вычислить, какую работу производит сила f={3; -2; -5}, когда ее точка приложения, двигаясь прямолинейно, перемещается из положения A(2; -3; 5} в положение B(3; -2; -1).

| |
| 816 | Даны силы  ={3; -4; 2}, ={3; -4; 2},  ={2; 3; -5}, ={2; 3; -5},  ={-3; -2; 4}, приложенные к одной точке. Вычислить, какую работу производит равнодействующая этих сил, когда ее точка приложения, двигаясь прямолинейно, перемещается из положения M1(5; 3; -7) в положение M2(4; -1; -4). ={-3; -2; 4}, приложенные к одной точке. Вычислить, какую работу производит равнодействующая этих сил, когда ее точка приложения, двигаясь прямолинейно, перемещается из положения M1(5; 3; -7) в положение M2(4; -1; -4).

| |
| 817 | Даны вершины четырехугольника A(1; -2; 2), B(1; 4; 0), C(-4; 1; 1), D(-5; -5; 3). Доказать, что его диагонали AC и BD взаимно перпендикулярны.

| |
| 818 | Определить, при каком значении  векторы векторы  и и  взаимно перпендикулярны. взаимно перпендикулярны.

| |
| 819 | Вычислить косинус угла, образованного векторами  ={2; -4; 4} и ={2; -4; 4} и 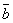 ={-3; 2; -6}. ={-3; 2; -6}.

| |
| 820 | Даны вершины треугольника A(-1; -2; 4), B(-4; -2; 0), C(3; -2; 1). Определить его внутренний угол при вершине В.

| |
| 821 | Даны вершины треугольника A(3; 2; -3), B(5; 1; -1), C(1; -2; 1). Определить его внешний угол при вершине А.

| |
| 822 | Вычислив внутренние углы треугольника с вершинами A(1; 2; 1), B(3; -1; 7), C(7; 4; -2), убедиться, что этот треугольник равнобедренный.

| |
| 823 | Вектор 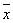 , коллинеарный вектору , коллинеарный вектору  ={6; -8; -7,5}, образует острый угол с осью Oz. Зная, что ={6; -8; -7,5}, образует острый угол с осью Oz. Зная, что  =50, найти его координаты. =50, найти его координаты.

| |
| 824 | Найти вектор 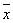 , коллинеарный вектору , коллинеарный вектору  ={2; 1; -1} и удовлетворяющий условию ={2; 1; -1} и удовлетворяющий условию  . .
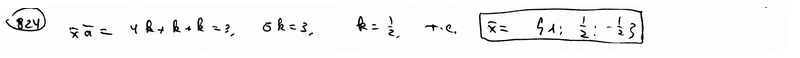
| |
| 825 | Вектор 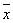 , перпендикулярный к векторам , перпендикулярный к векторам 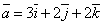 и и  , образует с осью Oy тупой угол. Найти его координаты, зная, что , образует с осью Oy тупой угол. Найти его координаты, зная, что  . .

| |
| 826 | Найти вектор 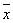 , зная, что он перпендикулярен к , зная, что он перпендикулярен к  ={2; 3; -1}, ={2; 3; -1}, 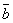 ={1; -2; 3} и удовлетворяет условию ={1; -2; 3} и удовлетворяет условию  . .

| |
| 827 | Даны векторы  ={3; -1; 5}, ={3; -1; 5}, 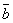 ={1; 2; -3}. Найти вектор ={1; 2; -3}. Найти вектор 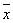 при условии, что он перпендикулярен к оси Oz и удовлетворяет условиям при условии, что он перпендикулярен к оси Oz и удовлетворяет условиям  , ,  . .

| |
| 828 | Даны векторы  , ,  и и  . Найти вектор . Найти вектор 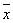 , удовлетворяющий условиям , удовлетворяющий условиям  , ,  , ,  . .
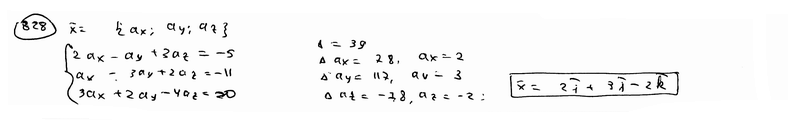
| |
| 829 | Найти проекцию вектора  ={4; -3; 2} на ось, составляющую с координатными осями равные острые углы. ={4; -3; 2} на ось, составляющую с координатными осями равные острые углы.

| |
| 830 | Найти проекцию вектора  ={ ={ 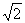 ; -3; -5} на ось, составляющую с координатными осями Ox, Oz углы ; -3; -5} на ось, составляющую с координатными осями Ox, Oz углы  , ,  , а с осью Oy – острый угол , а с осью Oy – острый угол  . .
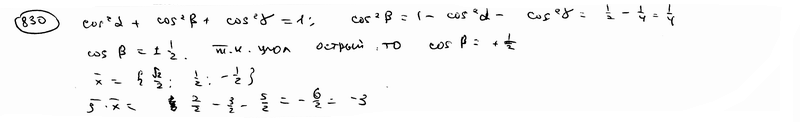
| |
| 831 | Даны точки A(3; -4; -2), B(2; 5; -2). Найти проекцию вектора  на ось, составляющую с координатными осями Ox, Oy углы на ось, составляющую с координатными осями Ox, Oy углы  , ,  , а с осью Oz – тупой угол , а с осью Oz – тупой угол  . .
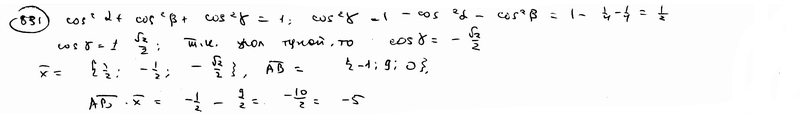
| |
| 832 | Вычислить проекцию вектора  ={5; 2; 5} на ось вектора ={5; 2; 5} на ось вектора 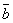 ={2; -1; 2}. ={2; -1; 2}.
| |
| 833 | Даны векторы  , , 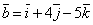 , ,  . Вычислить . Вычислить  . .

| |
| 834 | Даны векторы  ={1; -3; 4}, ={1; -3; 4}, 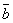 ={3; -4; 2} и ={3; -4; 2} и  ={-1; 1; 4}. Вычислить ={-1; 1; 4}. Вычислить  . .
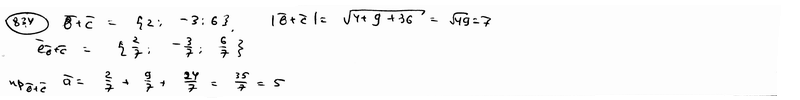
| |
| 835 | Даны векторы 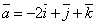 , ,  , ,  . Вычислить . Вычислить 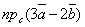 . .

| |
| 836 | Сила, определяемая вектором  ={1; -8; -7}, разложена по трем направлениям, одно из которых задано вектором ={1; -8; -7}, разложена по трем направлениям, одно из которых задано вектором  . Найти составляющую силы . Найти составляющую силы  в направлении вектора в направлении вектора  . .

| |
| 837 | Даны точки M(-5; 7; -6), N(7; -9; 9). Вычислить проекцию вектора  ={1; -3; 1} на ось вектора ={1; -3; 1} на ось вектора  . .

| |
| 838 | Даны точки A(-2; 3; -4), B(3; 2; 5), C(1; -1; 2), D(3; 2; -4). Вычислить  . .

|
|
из
5.00
|
Обсуждение в статье: Глава 31. Скалярное произведение векторов |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |
Популярное:
Личность ребенка как объект и субъект в образовательной технологии: В настоящее время в России идет становление новой системы образования, ориентированного на вхождение...
Модели организации как закрытой, открытой, частично открытой системы: Закрытая система имеет жесткие фиксированные границы, ее действия относительно независимы...
Почему люди поддаются рекламе?: Только не надо искать ответы в качестве или количестве рекламы...

©2015-2024 megaobuchalka.ru Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. (1462)
Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

