Глава 24. Приведение уравнения центральной линии второго порядка к простейшему виду

2015-11-20

1523

Обсуждений (0)

0.00 из 5.00 0 оценок

⇐ Предыдущая 8 9 10 11 121314 15 16 17 Следующая ⇒

		Определить тип каждого из следующих уравнений; каждое из них путем параллельного переноса осей координат привести к простейшему виду; установить, какие геометрические образы они определяют, и изобразить на чертеже расположение этих образов относительно старых и новых осей координат:;
	673.1
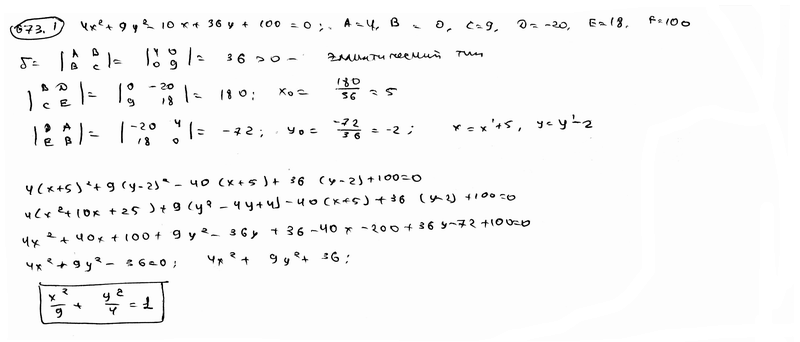
	673.2	;
	673.3	;
	673.4	;
	673.5	.
		Каждое из следующих уравнений привести к простейшему виду; определить тип каждого из них; установить, какие геометрические образы они определяют, и изобразить на чертеже расположение этих образов отноительно старых и новых осей координат:
	674.1	;
	674.2	;
	674.3	;
	674.4	;
	674.5	.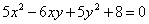
		Определить тип каждого из следующих уравнений при помощи вычисления дискриминанта старших членов:
	675.1	;
	675.2	;
	675.3	;
	675.4	;
	675.5	;
	675.6	.
		Каждое из следующих уравнений привести к каноническому виду; определить тип каждого из них; установить, какие геометрические образы они определяют; для каждого случая изобразить на чертеже оси первоначальной координатной системы; оси других координатных систем, которые вводятся по ходу решению, и геометрический образ, определяемый данным уравнением:
	676.1	;
	676.2	;
	676.3	;
	676.4	;
	676.5	: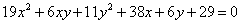
	676.6	.
		То же задание, что и в предыдущей задаче, выполнить для уравнений:
	677.1	;
	677.2	;
	677.3	;
	677.4	;
	677.5	;
	677.6	;
	677.7	;
	677.8	.
		Не проводя преобразования координат, установить, что каждое из следующих уравнений определяет эллипс, и найти величины его полуосей:
	678.1	;
	678.2	;
	678.3	;
	678.4	.
		Не проводя преобразования координат, установить, что каждое из следующих уравнений определяет единственную точку (вырожденный эллипс), и найти ее координаты:
	679.1	;
	679.2	;
	679.3	;
	679.4	.
		Не проводя преобразований координат, установить, что каждое из следующих уравнений определяет гиперболу, и найти величины ее полуосей:
	680.1	;
	680.2	;
	680.3	;
	680.4	.
		Не проводя преобразований координат, установить, что каждое из следующих уравнений определяет пару пересекающихся прямых (вырожденную гиперболу), и найти их уравнения:
	681.1	;
	681.2	;
	681.3	;
	681.4	.
		Не проводя преобразования координат, установить, какие геометрические образы определяются следующими уравнениями:
	682.1	:
	682.2	;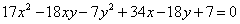
	682.3	;
	682.4	;
	682.5	.
		Для любого эллиптического уравнения доказать, что ни один из коэффициентов А и С не может обращаться в нуль и что они суть числа одного знака.
		Доказать, что эллиптическое уравнение второй степени ( 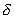>0) определяет эллипс в том и тольк в том случае, когда А и суть числа разных знаков.
		Доказать, что эллиптическое уравнение второй степени ( 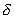>0) является уравнением мнимого эллипса в том и только в том случае, когда А и суть числа одинаковых знаков.
		Доказать, что эллиптическое уравнение второй степени ( 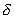>0) определяет вырожденный эллипс (точку) в том и только в том случае, когда =0.
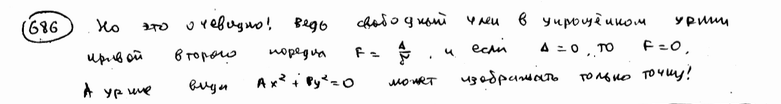
		Доказать, что гиперболическое уравнение второй степени ( 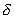<0) определяет гиперболу в том и только в том случае, когда .
		Доказать, что гиперболическое уравнение второй степени ( 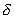<0) определяет вырожденную гиперболу (пару пересекающихся прямых) в том и только в том случае, когда =0.