Модели и алгоритмы дискретного программирования при управлении экономикой

Задача математического программирования, в которой одна или несколько переменных яв-ся целочисленными переменными наз-ся задачей дискретного программирования.

- задача полностью целочисленного программирования

- задача частичного целочисленного программирования

- задача булевого программирования, когда переменные принимают либо 0 либо 1.

Методы решения:

1. Методы округления. Имеющаяся задача решается другими методами и решение округляется.

2. Методы отсечения

3. Комбинаторно эвристические методы. (дерево поиска)

4. Выделение классов задач, в которых использование непрерывных методов дает автоматически целочисленное решение.

5. Специальные методы: 1)методы приближения и 2)методы случайного поиска.

Целочисленные и почтицелочисленные многогранники решения.

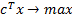
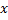– целое.

Многогранник с целочисленными вершинами – это целочисленный многогранник (М(А,b)).

Для того, чтобы многогранник был целочисленным, при векторе b необходимо и достаточно, чтобы А была абсолютна и унимодулярна (любой минор любого порядка должен принимать значение: -1, 0 ,1). . Матрица А с эл-ми абсолютно унимодулярна, если:

1.В любом столбце матрицы не более 2х отличающихся от «0» эл-та.

2.Все строки можно разбить на 2 подмножества и , обладающие свойствами:

а) если в некотором столбце эл-ты с одинаковыми знаками, то соответствующие строки в разных подмножествах.

б) если в некотором столбце эл-ты с разными знаками, то соответствующие строки в одном подмножестве.

Почтицелочисленные многогранники – целочисленные решения соответствуют вершинам, но среди вершин есть и нецелочиленные.

Методы отсечения в ЗЛП.

Алгоритм Роберта Гомори.

Требования к отсечению:

1. Должно отсекать нецелочисленное оптимальное решение.

2. Должно отсекать все целочисленные решения в допустимой области.

3. Должно быть линейным

4. Проходит через некоторую целочисленную точку.

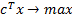
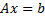
Используя симплекс метод нашли

– матрица:

– вектор: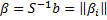

– нецелочисленная компонента

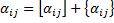
- отсечение Гомори.

- дополнительная переменная

Алгоритм:

1. Решая исходную задачу без ограничений на целочисленность (симплекс-метод)

2. Если решение целочисленное, то конец

3. Если решение нецелочисленное, то выбираем одну из нецелочисленных компонент i

4. Строим отсечение Гомори

5. Добавляем отсечение в систему ограничений задачи

6. Переходим на шаг 1.

Метод ветвей и границ.

Пусть , тогда:

Ветвления:

1. Специализированные (учитывающие специфику задач)

2. Универсальные (для любых задач):

a. Дихотомическое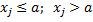

b. Покомпонентное

Границы:

1. Рекорд

2. Оценка 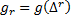- решается оценочная задача.

Требования к оценочной задаче:

1. Должна быть существенно более простая структура, чем исходная

2. Если 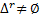, оценочная задача решения не имеет

3.

Алгоритм:

Строится множество кандидатов:

0)

1) Выбор кандидата:

2) Анализ кандидата: 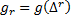- решается оценочная задача, рассчитывается оценка

3) , ⇒ шаг 5.

– целое число, то

, ⇒ шаг 5

4) Ветвление:

, ⇒ шаг 1

5) Анализ списка кандидатов: ⇒ конец, если 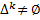⇒ , ⇒ шаг 1.