 |
Главная |
Для каких цепей справедлива методика расчета цепей несинусоидального тока, основанная на разложении ЭДС и токов источников в ряды Фурье?
|
из
5.00
|
ПРАКТИЧЕСКАЯ РАБОТА №9
Тема:Оценка результатов тестового эксперимента эффективности работы механизмов и оборудования на железнодорожном транспорте посредством определения сходимости числового ряда по признаку Даламбера.
Цель работы:Закрепить и систематизировать знания по теме: «Ряды».
Задание: Исследовать на сходимость числовой ряд с помощью теорем сравнения:
| 1. | 
| 4. | 
|
| 2. | 
| 5. | 
|
| 3. | 
| 6. | 
|
Задание: Исследовать на сходимость числовой ряд с помощью признака Даламбера:
| 7. | 
| 10. | 
|
| 8. | 
| 11. | 
|
| 9. | 
| 12. | 
|
Задание: Исследовать на сходимость числовой ряд с помощью признака Коши:
| 13. | 
| 16. | 
|
| 14. | 
| 17. | 
|
| 15. | 
| 18. | 
|
Задание: Найти сумму ряда:
| 19. | 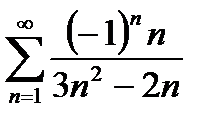 с точностью с точностью  . .
| 22. |  с точностью с точностью 
|
| 20. |  с точностью с точностью  . .
| 23. | 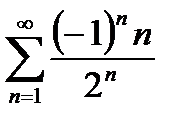 с точностью с точностью  . .
|
| 21. |  с точностью с точностью  . .
| 24. |  с точностью с точностью 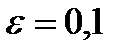 . .
|
Задание: Исследовать на сходимость числовой ряд с произвольными членами (в случае сходимости указать тип: абсолютная или условная):
| 25. | 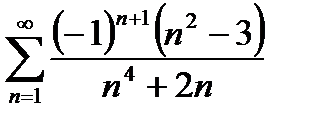
| 28. | 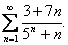
|
| 26. | 
| 29. | 
|
| 27. | 
| 30. | 
|
Пояснения к работе:
Необходимые формулы:
Признак сравнения
Пусть даны два ряда с положительными членами а1+ а2+…+ аn+… (А)
и b1+ b2+…+ bn+… (B), причем каждый член ряда (А) не превосходит соответствующего члена ряда (B), т.е. аnbn, начиная с некоторого номера, тогда:
1) если сходится ряд (B), то сходится и ряд (А);
2) если расходится ряд (А), то расходится и ряд (В).
Признак Даламбера
Если для ряда с положительными членами  существует
существует  , то при p<1 ряд сходится, при p>1 ряд расходится, при p=1 вопрос о сходимости остается открытым.
, то при p<1 ряд сходится, при p>1 ряд расходится, при p=1 вопрос о сходимости остается открытым.
Радикальный признак Коши
Если для ряда с положительными членами  существует
существует  , то при p<1 ряд сходится, при p>1 ряд расходится, при p=1 вопрос о сходимости остается открытым
, то при p<1 ряд сходится, при p>1 ряд расходится, при p=1 вопрос о сходимости остается открытым
Содержание отчета
1. Титульный лист в соответствии с СТП1.2-2005.
2. Цель работы
3. Задание
4. Выполненная практическая работа в соответствии с заданием
5. Ответы на контрольные вопросы
6. Вывод
Контрольные вопросы:
1. Запишите необходимое условие сходимости ряда.
2. Запишите теорему сравнения рядов.
3. Запишите интегральный признак Коши.
4. Запишите признак Лейбница.
5. Запишите ряды Тейлора и Маклорена.
ПРАКТИЧЕСКАЯ РАБОТА №10
Тема:Построение графа по условиям ситуационных задач: в управлении инфраструктурами на транспорте; в структуре взаимодействия различных видов транспорта.
Цель работы:Закрепить и систематизировать знания по теме: «Основы дискретной математики».
Задание: Выполните задание по теме: Граф и его элементы.
А) Запишите количество ребер и вершин графа;
В) Определить кратчайший путь из вершины 1 в вершину 8 для графа, представленного на рисунке;
С) Запишите номера вершин, имеющих одинаковую степень:
| 1. | 
| 4. | 
|
| 2. | 
| 5. | 
|
| 3. | 
| 6. | 
|
Задание: Выполните задание по теме: Граф и его элементы.
|
из
5.00
|
Обсуждение в статье: Для каких цепей справедлива методика расчета цепей несинусоидального тока, основанная на разложении ЭДС и токов источников в ряды Фурье? |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

