 |
Главная |
Вычисление площадей плоских фигур
|
из
5.00
|
Площадь криволинейной трапеции (рис.1) с основанием на оси ох вычисляется по формуле
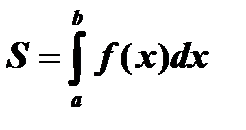
| y |
| x |
| 0 |

|

|

|
Рис. 1.
Если  , т.е. криволинейная трапеция расположена ниже оси ох (рис.2), то её площадь вычисляется по формуле
, т.е. криволинейная трапеция расположена ниже оси ох (рис.2), то её площадь вычисляется по формуле
| y |
| x |
| 0 |

|

|
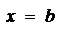
|
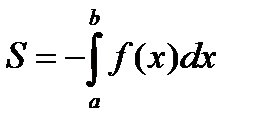
Рис. 2.
Если для всех 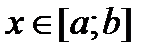 выполняется условие
выполняется условие 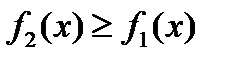 , т.е.
, т.е. 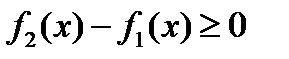 , то площадь фигуры, ограниченной графиками непрерывных функций
, то площадь фигуры, ограниченной графиками непрерывных функций  ,
, 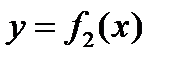 и прямыми
и прямыми 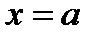 ,
,  ,
,  (рис.3), вычисляется по формуле
(рис.3), вычисляется по формуле
| y |
| x |
| 0 |

|

|

|

|

Рис. 3.
Площадь криволинейной трапеции с основанием на оси оу (рис.4) вычисляется по формуле:
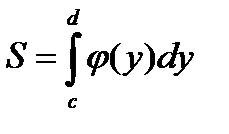
| y |
| x |
| 0 |
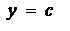
|
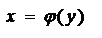
|
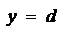
|
Рис. 4.
Если 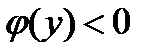 , т.е. криволинейная трапеция расположена левее оси оу (рис.5), то её площадь вычисляют по формуле
, т.е. криволинейная трапеция расположена левее оси оу (рис.5), то её площадь вычисляют по формуле

| y |
| x |
| 0 |
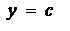
|
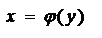
|
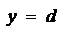
|
Рис. 5.
Если для всех 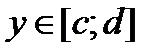 выполняется условие
выполняется условие 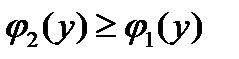 , т.е.
, т.е. 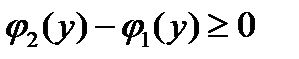 , то площадь криволинейной трапеции, ограниченной графиками непрерывных функций
, то площадь криволинейной трапеции, ограниченной графиками непрерывных функций  ,
, 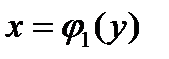 и прямыми
и прямыми  ,
,  ,
, 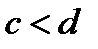 (рис.6), вычисляется по формуле
(рис.6), вычисляется по формуле
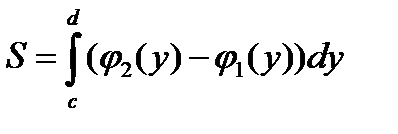
| y |
| x |
| 0 |
|
|
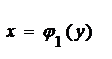
|

|
Рис. 6.
Вычисление объёмов тел вращения
Объём тела, образованного вращением вокруг оси ох криволинейной трапеции, ограниченной непрерывной линией 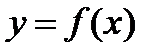 , отрезком оси абсцисс
, отрезком оси абсцисс  и прямыми
и прямыми 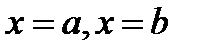 , вычисляется по формуле
, вычисляется по формуле
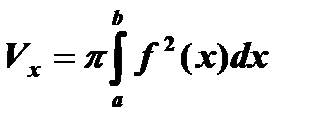 .
.
Объём тела, образованного вращением вокруг оси оу криволинейной трапеции, ограниченной непрерывной линией 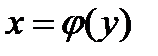 , отрезком оси ординат
, отрезком оси ординат  и прямыми
и прямыми  , вычисляется по формуле
, вычисляется по формуле
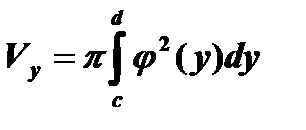 .
.
Содержание отчета
1. Титульный лист в соответствии с СТП1.2-2005.
2. Цель работы
3. Задание
4. Выполненная практическая работа в соответствии с заданием
5. Ответы на контрольные вопросы
6. Вывод
Контрольные вопросы:
1. Дайте определение неопределенного интеграла.
2. Запишите основные правила интегрирования.
3. Дайте определение определенного интеграла.
4. Запишите основные свойства определенного интеграла.
5. Запишите формулу Ньютона-Лейбница.
ПРАКТИЧЕСКАЯ РАБОТА №6
Тема:Решение дифференциальных уравнений первого порядка с разделяющимися переменными.
Цель работы:Закрепить и систематизировать знания по теме «Обыкновенные дифференциальные уравнения».
Задание: Проверить подстановкой, что данная функция является общим решением (интегралом) данного дифференциального уравнения:
| 1. | 1.  ; ; 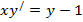
| 4. |  
|
| 2. | 1. 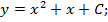 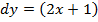
| 5. | 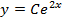 ; ; 
|
| 3. | 1. 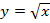 ; ; 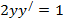
| 6. | 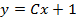 ; ; 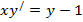
|
Задание: Найти общие решения дифференциальных уравнений методом разделения переменных:
| 7. | 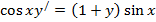
| 10. | 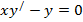
|
| 8. | 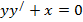
| 11. | 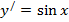
|
| 9. | 
| 12. | 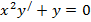
|
Задание: Найти частные решения уравнений первого порядка, удовлетворяющие указанным начальным условиям:
| 13. | 
| 16. | 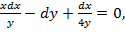
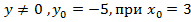
|
| 14. | 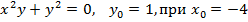
| 17. | 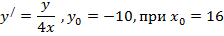
|
| 15. | 
| 18. | 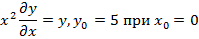
|
Задание: Решить линейные уравнения первого порядка:
| 19. | 
| 22. | 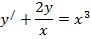
|
| 20. | 
| 23. | 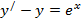
|
| 21. | 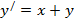
| 24. | 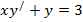
|
Задание: Найти частные решения однородных дифференциальных уравнений:
| 25. | 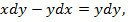
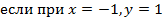
| 28. | 
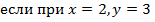
|
| 26. | 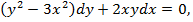
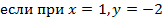
| 29. | 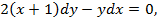
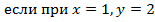
|
| 27. | 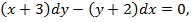
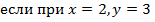
| 30. | 
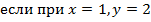
|
Пояснения к работе:
Необходимые формулы:
|
из
5.00
|
Обсуждение в статье: Вычисление площадей плоских фигур |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

