По какой формуле вычисляются касательные напряжения в произвольной точке поперечного сечения вала? Чему равны наибольшие касательные напряжения при кручении?

Подставив выражение (5.7) в формулу (5.4), получим:

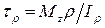. (5.8)

Формула (5.8) позволяет вычислить касательное напряжение в любой точке поперечного сечения вала.

Наибольшие касательные напряжения возникают в точках контура поперечного сечения при . Они равны:

.

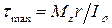Введя обозначение , окончательно получим:

. (5.9)

Величина 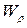называется моментом сопротивления при кручении (или полярным моментом сопротивления) и является геометрической характеристикой поперечного сечения вала. Момент сопротивления при кручении определяет способность вала сопротивляться кручению. Он измеряется в единицах длины в кубе (как правило, в см³).

Заметим, что буквенное обозначение W, выбранное для обозначения момента сопротивления при кручении, очень похоже на перевернутую букву M, что способствует лучшему запоминанию формулы (5.9).

Для стержня круглого поперечного сечения:

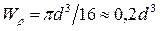. (5.10)

Для полого вала, имеющего внутренний диаметр d и внешний – D, полярный момент сопротивления равен:

,

где .

5.11. Как записывается условие прочности при кручении?

Прочность вала считается обеспеченной, если наибольшие касательные напряжения, возникающие в его опасном поперечном сечении, не превышают допускаемых касательных напряжений при кручении:

. (5.11)

Формула (5.11) служит для проверочного расчета вала на прочность.

Заметим, что незначительное превышение расчетного напряжения над допускаемым напряжением разрешается (не более 5 %).

При проектировочном расчете требуемый полярный момент сопротивления определяется по следующей формуле, вытекающей из условия прочности (5.11):

.

Отсюда легко можно найти требуемый диаметр вала. Например, для вала сплошного поперечного сечения, используя (5.10), получим:

. (5.12)

Для вала постоянного диаметра опасным является сечение, в котором возникает наибольший крутящий момент . Если же вал имеет переменное по длине поперечное сечение, то может оказаться, что наибольшие касательные напряжения возникают не там, где крутящий момент максимален. Следовательно, в этом случае вопрос об опасном сечении должен быть исследован дополнительно.

Допускаемое напряжение для пластичных материалов назначается в зависимости от их предела текучести при кручении (сдвиге):

.

Для хрупких материалов – в зависимости от предела прочности :

.

5.12. По какой формуле вычисляется угол закручивания вала?

Из (5.7) следует, что угол закручивания вала определяется по формуле

.

Если диаметр d постоянен по длине вала l и крутящий момент 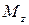имеет во всех поперечных сечениях одинаковое значение, то

.

5.13. Как записывается условие жесткости при кручении?

За меру жесткости при кручении принимается относительный угол закручивания вала . Условие жесткости имеет вид:

, (5.13)

где – значение допускаемого относительного угла закручивания, рад/м, которое зависит от назначения вала и условий его работы.

Если задано в град/м, то преобразовывать формулу (5.13) не следует. Проще просто перевести в рад/м, учитывая, что 1 рад » 57,3 град.

Неравенство (5.13) позволяет определить требуемый диаметр вала из условия жесткости. Так, для сплошного вала мы получим

. (5.14)

Напомним, что вал должен удовлетворять и условию прочности, и условию жесткости. Поэтому из двух значений диаметра, найденных нами по формулам (5.12) и (5.14), мы должны взять наибольшее значение.

5.14. По какой формуле вычисляется потенциальная энергия деформации при кручении вала?

При кручении, как и при других видах деформации стержня, работа внешней силы (скручивающего момента) расходуется на создание в деформируемом теле определенного запаса энергии (потенциальной энергии деформации), которая определяется по формуле (см. также беседу 15):

.