НАПРЯЖЕННОЕ СОСТОЯНИЕ В ТОЧКЕ ТЕЛА

С понятием о напряженном состоянии в точке тела мы уже встречались ранее. Так, в первой беседе мы обращали внимание Читателя на то, что нельзя говорить о напряжении в точке тела, не указывая положение площадки, на которой оно возникает, поскольку на различных площадках, проходящих через данную точку тела, могут возникнуть разные напряжения. Изучали мы напряженное состояние и в точке центрально растянутого (сжатого) стержня.

Ввиду того, что понятие о напряженном состоянии в точке тела является одним из ключевых понятий в курсе сопротивления материалов, считаем необходимым в этой беседе остановиться на этом вопросе более подробно.

6.1. Что понимается под напряженным состоянием в точке тела?

Напряженным состоянием (НС) в точке тела называют совокупность нормальных и касательных напряжений, возникающих на всевозможных площадках, проходящих через данную точку.

6.2. Какова конечная цель исследования НС в точке тела?

Для оценки прочности материала нас в первую очередь интересуют наибольшие значения нормальных и касательных напряжений, возникающих в данной точке тела. В дальнейшем мы установим, что для их определения нам необходимо знать нормальные и касательные напряжения на любых трех взаимно перпендикулярных площадках, проходящих через данную точку тела.

Кроме того, нам необходимо знать и направления «действия» этих наибольших нормальных и касательных напряжений или, иными словами, на каких площадках, проходящих через данную точку тела, они возникают.

Здесь и далее кавычки нами используются потому, что внутренние усилия не могут действовать, поскольку не являются активными силами.

6.3. С чего начинается исследование НС в некоторой точке тела?

Оно начинается с того, что в окрестности исследуемой точки, например точки К (рис. 6.1), из нагруженного тела, находящегося в равновесии, мысленно вырезается элементарный параллелепипед со сторонам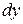и , и . Ввиду малости этого параллелепипеда можно считать, что НС во всех его внутренних точках одинаково (то есть однородно) и совпадает с НС в непосредственно исследуемой точке К. Поэтому мы будем предполагать, что как по граням, так и по любым другим сечениям элементарного параллелепипеда нормальные и касательные напряжения распределяются равномерно.

Эти предположения позволяют нам исследовать закон изменения напряжений по наклонным сечениям элементарного параллелепипеда, считая, что эти сечения проходят через исследуемую нами точку К.

6.4. Какие различают виды НС в точке тела?

В дальнейшем мы увидим, что в окрестности любой точки деформированного твердого тела всегда можно выделить элементарный параллелепипед, ориентированный в пространстве таким образом, что по его граням будут возникать только нормальные напряжения. В зависимости от того, испытывает ли такой параллелепипед «растяжение» («сжатие») в одном, в двух или в трех направлениях, различают следующие виды НС (рис. 6.2).

С линейным НС мы уже сталкивались при изучении центрального растяжения (сжатия) стержня.

В задачах сопротивления материалов наиболее часто встречается плоское НС. Его характерным признаком является полное отсутствие нормальных и касательных напряжений на двух параллельных гранях элементарного параллелепипеда.

Именно этому случаю НС мы и уделим в дальнейшем основное внимание. В частности, мы будем полагать, что напряжения не возникают на гранях элементарного параллелепипеда с нормалью x.Тогда вместо объемного параллелепипеда, с целью упрощения, мы будем на рисунках показывать плоский элемент, то есть проекцию параллелепипеда на плоскость 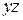. При этом штриховкой мы будем указывать внутреннюю область этого элемента.

Объемное НС в курсе сопротивления материалов практически не изучается.

6.5. Какие правила знаков для нормальных и касательных напряжений принимаются в сопротивлении материалов при изучении плоского НС?

Установим следующие правила знаков.

Для нормальных напряжений оно формулируется очень просто: нормальное напряжение, соответствующее растяжению, считается положительным, а сжатию – отрицательным.

Несколько сложнее выглядит правило для касательных напряжений.

Касательное напряжение будем считать положительным, если одновременно выполняются (или одновременно не выполняются) следующие два условия:

· во-первых, направление напряжения совпадает с положительным направлением соответствующей координатной оси;

· во-вторых, внешняя нормаль к площадке, на которой оно возникает, направлена в ту же сторону, что и другая соответствующая координатная ось.

Например, все напряжения на рис. 6.3, возникающие по граням элементарного параллелепипеда, показаны положительными. Поскольку, как уже отмечалось, во всех точках элементарного параллелепипеда НС считается однородным, одноименные напряжения, возникающие на параллельных гранях элемента, численно равны друг другу.

Отметим, что при анализе НС в некоторой точке тела нормальные и касательные напряжения, возникающие по граням элементарного параллелепипеда, считаются заданными.

6.6. Как формулируется закон парности касательных напряжений?

Элементарный параллелепипед должен находиться в равновесии. В частности, он не должен вращаться вокруг оси x, проходящей через точку К (см. рис. 6.3), поэтому суммарный момент всех сил, возникающих по его граням, относительно этой оси должен быть равен нулю:

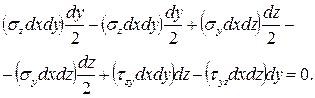(6.1)

В формуле (6.1) в скобки заключены соответствующие силы, а их плечи указаны за скобками.

После элементарных упрощений выражения (6.1) найдем:

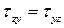. (6.2)

Соотношение (6.2) и называется законом парности касательных напряжений: на любых двух взаимно перпендикулярных площадках касательные напряжения, направленные по перпендикуляру к линии пересечения этих площадок, равны по величине. При этом касательные напряжения либо сходятся к линии пересечения площадок, либо расходятся от нее.