 |
Главная |
Симплекс алгоритм. Процесс приближения к оптимуму (направленный перебор краевых вершин)
|
из
5.00
|
Пусть задача представлена в К В, соответственно сразу получаем некое исходное базисное решение.
Возникают следующие вопросы:
- Оптимально ли и единственно ли оно;
- Если не оптимально, а ранее мы показали, что поиск решения состоит в переборе краевых вершин, то возникает вопрос, как осуществить переход к следующему решению.
Вспоминая, что целевая функция выглядит следующим образом:
n
Z=Σ СjXj
j=1
Просуммируем соответствующие уравнения в системе (2) умножив их на коэффициент Сj.
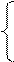 C1x1 + a1m+1xm+1 + … + a1nxn = C1B1
C1x1 + a1m+1xm+1 + … + a1nxn = C1B1
…
Cmxm + amm+1xm+1 + … + amnxn = CmBm
Имеем:
n n m
∑ СjXj + ∑ СjXj = Z0 + ∑ СjXj (3)
j=1 j=m+1 j=m+1
Где C j - коэффициент при свободных переменных и зависит от значения aij , Вi. По своему смыслу Z0 есть значение целевой функции для исходного базисного решения.
Теорема:
Допустимое базисное решение xi = Вi при i = 1…m, xj = 0 при j = m+1…m, является оптимальным, если коэффициенты Cj в выражении (3) не отрицательны.
Доказательство:
Если переменные C ≥ 0, то при любых значениях (не отрицательных) переменных xj , разность Z и Z0 неотрицательна и ее минимум есть 0, следовательно, Z не будет меньше Z0, что говорит о том, что его нельзя уменьшить.
Следствия:
n
- Любое решение системы (1), которому соответствует нулевая сумма (Σ СjXj) при
j=m+1
любых Cj ≥0 и xj ≥0 будет оптимальным, соответственно при существовании C j < 0, решение может быть улучшено.
- Допустимое оптимальное базисное решение окажется единственным, если все C j > 0 (строго больше).
Данные следствия являются сформулированными признаками оптимальности и единственности оптимального решения.
Теперь рассмотрим, как осуществить переход к новому решению и сформулируем критерий оптимальности выбора направления перехода.
Пусть среди коэффициентов C j есть отрицательные значения, это значит, что давая приращения, соответственным переменным, целевую функцию можно уменьшить, чтобы перейти к другому целевому решению (как следует из интерпретации) необходимо сделать положительной (ввести в базис) какую-то из переменных xn+1 = … =xn = 0, обратив в 0 одну из переменных x1…xn . соответственно в базис должно вводиться та переменная (ей дается положительное приращение), которая имеет в выражении для целевой функции отрицательный коэффициент.
Обозначим через S тот номер j из n+1,…,n величина коэффициента C j для которого отрицательна и максимальна по модулю.
Cs=min[C j <0]
Отсюда бросается в глаза очевидный подход к поиску оптимального решения, который и используется в С А.
Соответственно будем давать положительное приращение к переменной Xs . Давая данное приращение, из уравнений (2), получаем:
 x1 = B1 - a1s xs
x1 = B1 - a1s xs
…
xm = Bm - ams xs
Для Z имеем:
Z = Z0 + Сs Xs (Сs < 0)
Естественно, что выбрав направление движения, целесообразно максимально увеличить переменную Xs, чтобы получить максимальное выражении в значении целевой функции. Однако возрастание переменной Xs ввиду требования к неотрицательной переменной возможно до тех пор, пока какая-то из свободных переменных не обратиться в ноль, то есть, пока не достигнем граничного значения.
Это произойдет если хотя бы один коэффициент с индексом Xs положителен по условию и среди Вi нет отрицательных. Если все ais положительны, то первая в 0 обратиться та базисная переменная, для которой будет выполняться:
Xs = min [Вi / ais]
Это и есть формализованное условие перехода к последующей краевой вершине.
Симплекс метод.
Ранее было показано, что СА предполагает направленный перебор краевых вершин. Мы определились с тем, каким образом осуществлять данный перебор, как выбрать направления перебора, как определить, что в итоге получено оптимальное решение (все это ранее было выражено в формальном виде – приведены соответствующие формулы для расчетов).
Однако остается проблема, состоящая в том, как найти то первое допустимое решение (а это должна быть краевая точка), с которой начинать направленный перебор вершин (т.е. когда уже становится возможным применение СА). Для это цели и служит СМ, состоящий в двухэтапном решении задачи. На первом этапе требуется найти какое-либо решение задачи (исходную краевую точку), на втором – осуществить перебор вершин с целью поиска оптимального решения. При этом будем помнить, что краевая точка легко отыскивается, в случае представления задачи в КВ (см. выше).
С М предполагает в общем случае двухэтапного применения С А.
Первый этап начинают с формального введения в каждую строку стандартной системы искусственной неотрицательной переменной для получения К В (напомним, что при представлении задачи в данном виде сразу же можно определить решение задачи).
Исходная:
 a11x1 + … + a1nxn = b1
a11x1 + … + a1nxn = b1
a1mx1 + … + amnxn = bm
К В:
 a11x1 + … + a1nxn + xn+1= B1
a11x1 + … + a1nxn + xn+1= B1
a1mx1 + … + amnxn + xn+m= Bm
Однако этим мы изменили собственно задачу. В каком случае решение новой задачи и исходной задачи будут совпадать?
Если существует решение для первой задачи, то оно допустимо и для второй при условии xn+1 = … =xn+m = 0 (т.к. именно эти переменные были нами введены, ввиду их неотрицательности, при данном условии все переменные обращаются в 0).
Рассмотрим сумму (W= xn+1 + …+ =xn+m ) наименьшее значение которой есть 0 ввиду неотрицательности переменных при xn+1 = … =xn+m = 0. Таким образом, проверка условия minW=0 для второй системы ограничений, является условием совпадения решения для первой и второй задач.
С учетом сказанного, первый этап решения С М состоит в поиске какого-либо решения исходной задачи, по средствам решения следующей оптимизационной задачи:
m
minW=Σ xn+j .
j=1
с учетом ограничений (системы), заданных для второй задачи.
Для данной задачи, приведенной к К В (то есть может быть применен С М), легко находится первое решение. xn+1 = В1, …, xn+m =Bm , а x1 =…= xn =0. После чего может быть использован С А с целью поиска оптимального решения. Если удается найти оптимальное решение, для которого W=0, это решение является исходным для основной задачи. В противном случае задача не разрешима.

Второй этап состоит в решении основной задачи, в использовании С А уже для решения основной задачи, при этом получим решение вспомогательной задачи рассмотренное как исходное для основной, проверяется на оптимальность при необходимости осуществления последовательного перебора решений (Замечание: здесь уже используется целевая функция Z).
|
из
5.00
|
Обсуждение в статье: Симплекс алгоритм. Процесс приближения к оптимуму (направленный перебор краевых вершин) |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

