 |
Главная |
Векторная интерпретация задачи. Место эвристики
|
из
5.00
|
На практике практически отсутствуют системы, характеризуемые одним единственным параметром, который может рассматриваться в качестве критерия оптимальности. Поэтому для сравнительного анализа необходимо учитывать одновременно несколько параметров, характеризуемых разнородностью (производительность, надежность, стоимость, габариты и т.д. и т.п.) Как же произвести подобное сравнение? С этой целью используются методы многокритериальной оптимизации.
Данный класс задач предполагает сравнение вариантов решения одновременно по нескольким параметрам, где каждый n–ый вариант характеризуется m-ым числом параметров:
n, n=1,N
m, m=1,M
(qnm, n=1,N, m=1,M – в общем случае некая функция)
Для сравнения вариантов между собой необходимо сведение задачи к однокритериальной. Существует два основных подхода, различающихся типом «свертки» параметров.
Это мультипликативная и аддитивная свертка.
M
Фn = П qnm – мультипликативная
m=1
N
 Yn = ∑ qnm - аддитивная
Yn = ∑ qnm - аддитивная
n=1
Первый подход предполагает простое перемножение параметров между собою. Не говоря об отсутствии обоснованного физического смысла (производительность умножается на надежность) данный подход характеризуется следующим огромным недостатком – существенная зависимость агрегатирующего критерия оптимальности от отдельных локальных качеств (если умножить на 0, то результатом будет 0).
В связи с этим на практике широкое применение нашла аддитивная свертка. Для ее применения необходимо решить два вопроса:
1. Как учесть разный физический смысл (природу) различных параметров.
2. Как учесть различную относительную важность разнородных параметров.
Дадим векторную интерпретацию задачи. Рассмотрим данную задачу на плоскости:
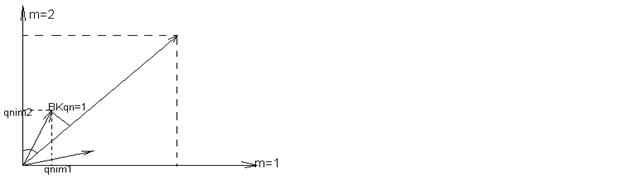
Каждый вариант решения на плоскости образует вектор качества. В рамках данной интерпретации получаем, что вариант решения характеризуется длиной вектора качества и величиной угла с неким идеальным вектором, или длиной проекции на идеальный вектор:
 |Xn|→max
|Xn|→max
→ Xno=Xn cosαno
αno→min
Т.е., в предположении, что задан некоторый идеальный вектор качества (qn=0), лучший вариант можно определить по длине вектора и углу вектора с идеальным. Или сводя задачу к однокритериальной по длине проекции вектора качества на идеальный вектор. Ранее мы показывали, что в ортонормированном базисе данная длина определяется следующей функцией:
M N

 Xm = (1/√M)*∑qnm = Yn = ∑qnm
Xm = (1/√M)*∑qnm = Yn = ∑qnm
m=1 n=1
а это ни что иное, как аддитивная свертка.
Таким образом, аддитивный критерий оптимальности может интерпретироваться как приведенная (умноженная на коэффициент 1/√M) длина проекции вектора качества варианта на идеальный вектор качества.
Возникают 2 вопроса:
1. Как задать идеальный вектор (соответственно, как нормировать параметры).
2. Как учесть относительную важность разнородных параметров.
Рассмотрим альтернативные варианты решения.
|
из
5.00
|
Обсуждение в статье: Векторная интерпретация задачи. Место эвристики |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

