 |
Главная |
ОЦЕНКА ДОСТОВЕРНОСТИ СРЕДНИХ И ОТНОСИТЕЛЬНЫХ ВЕЛИЧИН
|
из
5.00
|
При оценке достоверности средних или относительных величин руководствуются следующим правилом:средняя арифметическая или относительная величина при числе наблюдений в выборочной совокупности 30 и более должны превышать свою ошибку не менее чем в 2 раза.
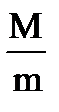 > 2или
> 2или 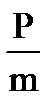 > 2
> 2
В рассматриваемых примерах средняя арифметическая, характеризующая рост восьмилетних мальчиков и показатель „индекс здоровья” превышают свои ошибки соответственно:
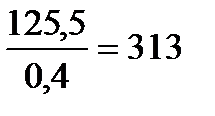 раз,
раз, 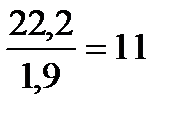 раз, что соответствует высокой степени их статистической достоверности с вероятностью более чем 99,7 %.
раз, что соответствует высокой степени их статистической достоверности с вероятностью более чем 99,7 %.
Высказанное положение вытекает из теории «вероятности», под которой понимается числовая мера объективной возможности появления случайного события.
Вероятность - число, которое находится между 0 и 1, или между 0% и 100%. Математиками определено, что той или иной вероятности, выраженной в процентах, соответствует определенное значение критерия t Стьюдента.
Так, например, вероятности равной Р = 68,3% соответствует t= 1,0,
вероятности равной Р = 95,5 %соответствуетt = 2,0
вероятности равнойР = 99,7 %соответствуетt = 3,0 .
В медико-биологических исследованиях событие является статистически достоверным, если вероятность его появления соответствует значению критерия t Стьюдента, равное 2.
Средняя ошибка позволяет не только оценить достоверность относительного показателя или средней величины, но и найти доверительные границы средней величины или относительного показателя в генеральной совокупности
М ген.= М выб. ± t * m
Р ген. = Р выб . ± t *· m
Как уже было сказано, величина средней ошибки указывает, насколько средняя величина и относительный показатель выборочной совокупности отличаются от соответствующих величин в генеральной совокупности. Величина t*m является тем доверительным интервалом по отношению к средней или относительной величине, в котором с определенной степенью вероятности можно ожидать нахождение средней или относительной величины в генеральной совокупности.
Пример 10.
М выб .= 125,5 см; m = ± 0,4 см.
При 95% вероятности t =2, при 99,7 % - t = 3 .
М ген.= 125,5 см ± 2 · 0,4 см = 124,7 - 126,3 см
М ген.= 125,5 см ± 3 · 0,4 см = 124,3 - 126,7 см.
Таким образом, с вероятностью 95% можно ожидать, что средняя будет находиться в пределах от 124,7 до 126,3 см и с вероятностью 99,7% - в пределах от 124,3 до 126,7 см.
Понятно, что действительное значение средней можно получить только при обследовании всех 8-летних мальчиков, но как это очевидно из полученных данных, подобное исследование нецелесообразно, т.к. средняя арифметическая статистически достоверна (Р > 99,7%), а доверительный интервал для средней в генеральной совокупности является весьма незначительным -t*m- = 3*0,4 т.е. всего по 1,2 см от средней выборочной совокупности в большую и меньшую сторону.
|
из
5.00
|
Обсуждение в статье: ОЦЕНКА ДОСТОВЕРНОСТИ СРЕДНИХ И ОТНОСИТЕЛЬНЫХ ВЕЛИЧИН |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

