Тесты для самоконтроля. 1. Достоверность средней арифметической величины зависит от следующих элементов

 

1. Достоверность средней арифметической величины зависит от следующих элементов (верно все, кроме одного):

1. колеблемость ряда

2. условная средняя

3. её ошибка

4. среднее квадратическое отклонение

2. Достоинство средней величины состоит в том, что она позволяет

1. анализировать большое число наблюдений

2. выявить закономерности при малом числе наблюдений и большом разбросе показателей

3. с помощью одного числа получить представление о совокупности массовых явлений

3. Мерилом достоверности средней и относительной величины является

1. среднее квадратическое отклонение

2. размах вариации

3. ошибка репрезентативности

4. коэффициент вариации

4. Процентное отношение среднего квадратического отклонения к средней арифметической - это

1. ошибка репрезентативности

2. условная средняя

3. доверительный коэффициент

4. коэффициент вариации

5. критерий достоверности разности

5. Граница генеральной совокупности при заданной степени вероятности характеризует

1. среднее квадратическое отклонение

2. степень вариации

3. доверительный коэффициент

4. ошибка

5. доверительный интервал

6. При расчете доверительных границ средней и относительной величины при числе наблюдения n<30 доверительный коэффициент (t) определяется

1. по специальной формуле

2. по таблице со специальным коэффициентом

3. по таблице Стьюдента

4. с помощью коэффициента

7. Для медицинских исследований достаточной степенью вероятности является (%)

1. 75

2. 99,9

3. 95,0

4. 68

8. Разность сравниваемых величин существенна, если

1. t >=1

2. t >=2

3. t <=2

9. За условную среднюю можно принять

1. моду

2. моду, медиану

3. моду, медиану, любую варианту ряда

4. моду, медиану, любую варианту ряда, любое числовое значение

5. моду, медиану, любую варианту ряда, любое числовое значение, доверительный коэффициент

10. Для определения ошибки средней величины при большом числе наблюдений используется:

1. m =

2.

3. m = ±

4.

11. Средняя арифметическая по способу моментов равна:

1. полусумме крайних показателей вариационного ряда

2. любой варианте ряде плюс среднее отклонение от нее всех вариант

3. наименьшей варианте ряда плюс среднее отклонение от нее всех вариант

12. Ошибка средней арифметической величины показывает

1. в каких пределах могут колебаться полученные средние арифметические величины

2. как отличается максимальный показатель ряда от средней арифметической величины

3. как отличается минимальный показатель ряда от средней арифметической величины

4. степень вероятности результата

13. Для вычисления средней арифметической взвешенной применяется формула:

1. M =

2. M =

3. M = М₁ +

4. M = М₁ + i

14. Для оценки достоверности разности сравниваемых относительных величин используется формула:

1.

2. t =

3. t =

4.

15. Установить соответствие

Степень разнообразия признака	Величина коэффициента вариации
1. сильная	а) 15-25
2. средняя	б) до 15
3. слабая	в) до 10
	г) 10-15
	д) 10-20
	е) более 20

Ключ к тестам:

№ вопроса	Ответ
	2, 3
	1- Е; 2 - Д; 3 - В

 

КРИТЕРИЙ СООТВЕТСТВИЯ ( 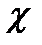²) - «ХИ-КВАДРАТ»

С помощью ² (хи-квадрат) определяют соответствие (согласие) эмпирического распределения теоретическому, и тем самым оценивают достоверность различий между выборочными совокупностями. Критерий применяется в тех случаях, когда нет необходимости знать величину того или иного параметра (среднюю или относительную величину) и требуется оценить достоверность различий не только двух, но и большего числа групп.

Критерий соответствия применяется для статистической оценки результатов исследования в случаях, когда нет необходимости знать величину самого показателя, размер связи, а требуется лишь подтвердить, существенно ли влияние изучаемого фактора или оно случайно, и подтвердить наличие взаимосвязи между явлениями. В отличие от метода оценки достоверности по критерию Стьюдента, который позволяет проводить только попарное сравнение, критерий соответствия применяется для сопоставления не только двух, но и большего числа групп, в этом его преимущество. Определение критерия соответствия основано на довольно распространенном в исследованиях приеме: доказывать от противного.

В практическом здравоохранении метод ² может широко использоваться при оценке эффективности прививок, действия препаратов, результатов различных методов лечения и профилактики заболеваний влияния условий труда и быта на заболеваемость работающих. С помощью критерия можно определить, влияют или нет сроки госпитализации на течение заболеваемости, влияет ли материальное обеспечение населения на уровень заболеваемости и т.д. Критерий определяется по формуле:

² =

где Р - фактические (эмпирические) данные;

Р₁ - «ожидаемые» (теоретические) данные, вычисленные на основании нулевой гипотезы;

- знак суммы.

Определение критерия основано на расчете разницы между фактическими и «ожидаемыми» данными. Чем больше эта разность (Р - Р₁), тем с большей вероятностью можно утверждать, что существуют различия в распределении сравниваемых выборочных совокупностей, и наоборот, чем меньше разность, тем меньше шансов на то, что сравниваемые выборочные совокупности различны между собой.

Пример.При изучении организации специализированной помощи больным ревматизмом (табл. 1) были проанализированы сроки постановки диагноза с момента обращения в поликлинику (менее 15 дней, 15 дней и более) 73 пациентов поликлиники №1, где прием больных вел специалист в кардиоревматологическом кабинете, и 21 пациента поликлиники № 2, где специализированного кабинета не было (прием вел терапевт).

Определите, существенно ли различаются группы больных ревматизмом по срокам постановки диагноза с момента обращения в поликлинику в зависимости от наличия в поликлинике кардиологического кабинета.

Последовательность решения:

1 этап- распределение фактических данных (Р) по всем группам, суммирование итогов 61+33=94.

2 этап- определение ожидаемых величин (Р₁) на основе «нулевой гипотезы». Согласно «нулевой гипотезе», допускают, что наличие или отсутствие в поликлинике кардиоревматологических кабинетов не влияет на сроки постановки диагноза у больных ревматизмом. В этом случае распределение двух групп больных, обслуживаемых с участием специалистов кардиоревматологического кабинета и без него, по срокам постановки диагноза должно быть одинаковым и соответствовать итоговому фактическому распределению всех наблюдаемых больных, т.е. 61 и 33. При таком условии в первой группе (кардиоревматологический кабинет есть) «ожидаемое» число больных со сроком установления диагноза менее 15 дней определяется по следующей пропорции:

94 - 61

73-х х = 47,4

«Ожидаемое» число больных со сроком установления диагноза 15 дней и более получается путем вычисления 73 - 47,4=25,6. Подобным же образом рассчитывают «ожидаемые» числа больных второй группы. Полученные «ожидаемые» числа по всем группам заносят в таблицу.

3 этап- определяют разность между фактическими и «ожидаемыми» числами (Р - Р₁).

Первая группа больных (Р - Р₁) = 54 - 47,4 = +6,6;

19-25,6= -6,6.

Вторая группа больных (Р - Р₁) = 7-13,6=-6,6;

14-7,4=+6,6 (в числовом отношении разность между фактическими и «ожидаемыми» числами (Р - Р₁) одинакова, что позволяет проверить правильность расчетов).

4 этап- определяют квадрат разностей (Р- Р₁)² по всем группам.

5 этап- квадрат разности делят на ожидаемое число во всех группах и результаты заносят в таблицу, например, 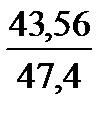= 0,9 и т.д.

6 этап- критерий соответствия определяется путем суммирования предыдущих результатов по всем группам:

² = = 0,9+1,7+3,2+5,9 = 11,7.

Таблица 1

Распределение больных ревматизмом по срокам установления диагноза в поликлиниках с разной системой организации специализированной помощи

 

Кардио- ревматологический кабинет	Число больных	1 этап	2 этап	3 этап	4 этап	5 этап
Р	Р1	Р-Р1	(Р-Р1)2
<15 дней	15 и >	<15 дней	15 и >	<15 дней	15 и >	<15 дней	15 и >	<15 дней	15 и >
Есть				47,4	25,6	+6,6	-6,6	43,56	43,56	0,9	1,7
Нет				13,6	7,4	-6,6	+6,6	43,56	43,56	3,2	5,9
Итого

Величина критерия 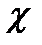² зависит от величины разности между фактическими и «ожидаемыми» числами и от числа слагаемых (т.е. числа сравниваемых групп по графам и строкам). Чем большеразность, тем больше критерий. Если бы фактические данные были равны «ожидаемым», то х был бы равен нулю и «нулевую гипотезу» надо было бы признать существенной, и, наоборот, чем больше величина критерия, тем «нулевая гипотеза» становится менее вероятной, несущественной.

Для оценки критерия учитывают число рядов (R) и число строк (S) распределения фактических чисел (без итоговых) и на основании этих данных вычисляют так называемое число степеней свободы n' = (R-1) • (S-1). В нашем примере R=2, S=2, при этом n'= (2-1) • (2-1)=1. Число степеней свободы указывает на число «свободно варьирующих» элементов, или число клеток таблицы, которые могут быть заполнены любыми числами без изменения общих итоговых данных.

Полученную величину оценивают по специальной таблице (прил. 3). Для того, чтобы опровергнуть «нулевую гипотезу», вычисленный критерий соответствия должен быть равен или больше табличного (критического) значения 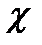² при уровне вероятности «нулевой» гипотезы р = 5%.

При альтернативном распределении применяется упрощенная формула расчета 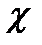² на основе таблицы взаимной сопряженности (четырехпольной таблицы):

	p2	q2	Всего
p1	а	с	а + с
q1	b	d	b + d
Всего	а + b	с + d	a + b + c + d

 

Величину 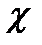² можно оценить и без таблицы, по упрощенной формуле: если больше 3, то «нулевая гипотеза» отвергается.

² =

где р, q — значения альтернативных признаков в обеих группах;

а, b, с, d — абсолютные величины в клетках таблицы.

ЭТАЛОН РЕШЕНИЯ(по «четырехпольной таблице»):

1. Согласно «нулевой гипотезе» допускаем, что наличие или отсутствие в поликлинике кардиоревматологических кабинетов не влияет на сроки постановки диагноза у больных ревматизмом.

2. Составляем «четырехпольную таблицу»

Наличие кардиологического кабинета в поликлинике	Срок постановки диагноза менее 15 дней (р)	Срок постановки диагноза 15 дней и более (q)	Всего
Есть кабинет (р)	54 (а)	19 (с)
Кабинета нет (q)	7(b)	14 (d)
Всего

² = =

= = 11,8.

3. Оцениваем число степеней свободы. В нашем примере имеется только одно число степеней свободы n = 1. Это указывает на то, что достаточно найти только одно «ожидаемое» число, тогда три остальных числа можно легко получить как дополнение до итоговых чисел.

4. Полученную величину критерия при n = 1 оценивают по специальной таблице (приложение 1). Вычисленная нами величина 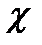^{2 =} 11,8 больше критического значения 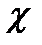²,при котором уровень ее вероятности подтверждения «нулевой гипотезы» будет равен 0,1%. Это дает основание опровергнуть «нулевую гипотезу» и признать существенными различия в распределении по срокам постановки диагноза двух сравниваемых групп (обследованных специалистом, работающим в кардиоревматологическом кабинете, и при отсутствии такого специалиста).

5. Следовательно, на основании проведенного исследования можно утверждать, что организация специализированных кардиоревматологических кабинетов в поликлиниках позволяет снизить сроки обследования больных ревматизмом.

Приложение 1

Таблица оценки значений критерия соответствия 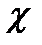²

n - 1	Уровень вероятности подтверждения «нулевой гипотезы»
5%	1%	0,1%
	3,8	6,6	10,8
	6,0	9,2	13,8
	7,8	11,3	16,3
	9,5	13,3	18,5
	11,1	15,1	20,5
	12,6	16,8	22,5
	14,1	18,5	24,3
	15,5	20,1	26,1
	16,9	21,7	27,9
	18,3	23,2	25,6
	19,6	24,7	31,3
	21,0	26,2	32,9
	22,4	27,7	34,5
	23,7	29,1	36,1
	25,0	30,6	37,7
	26,3	32,0	39,3
	27,6	33,4	40,8
	28,9	34,8	42,3
	30,1	36,9	43,8
	31,4	37,6	45,3
	32,7	38,9	46,8
	33,9	40,3	48,7
	35,2	41,6	49,7
	36,4	43,0	51,2
	37,6	44,3	52,6
	38,9	45,6	54,1
	40,1	47,0	55,5
	41,3	48,3	56,9
	42,6	49,6	58,3
	43,8	50,9	59,7

 

Контрольные вопросы

1. С какой целью применяются критерий соответствия?

2. Укажите условия применения критерия соответствия?

3. Что означает понятие «нулевая гипотеза»?

4. Какими критериями необходимо пользоваться при выборе того или иного непараметрического метода оценки достоверности?

5. Возможно ли применение критерия соответствия для относительных величин и средних?

6. Как определить число степеней свободы при вычислении критерия соответствия?

7. Укажите достоинства и недостатки критерия соответствия.

8. Пользуясь таблицей критерия соответствия, назовите подтверждение или опровержение «нулевой гипотезы при

n = 2 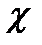² = 14

n = 3 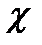² = 7,2

n = 4 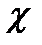² = 9,7

n = 6 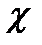² = 17

n = 2 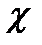² = 6,3

9. Можно ли оценить величину 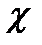² без таблицы? Каковы критерии оценки?