 |
Главная |
Теоретические сведения. Лабораторная работа №1
|
из
5.00
|
Лабораторная работа №1
Построение модели линейной парной регрессии, анализ статистической значимости и выполнение прогноза
Цель: провести спецификацию модели; оценить параметры линейной парной регрессии; проанализировать статистическую значимость результатов регрессионного моделирования и качество линейного уравнения парной регрессии; оценить тесноту связи фактора с результативным признаком; выполнить прогнозирование; интерпретировать результаты; проверить полученные результаты с помощью ППП MS Excel.
Теоретические сведения
Парная регрессия – уравнение связи двух переменных у и х:  ,
,
где у – зависимая переменная (результативный признак); х – независимая, объясняющая переменная (признак - фактор). Различают линейные и нелинейные регрессии. Линейная регрессия: 
Любое эконометрическое исследование начинается со спецификации модели, т.е. с формулировки вида модели, исходя из соответствующей теории связи между переменными. В парной регрессии выбор вида математической функции  может быть осуществлен тремя методами: графическим; аналитическим; экспериментальным. Аналитический метод основан на изучении материальной природы связи исследуемых признаков. Экспериментальный метод основан на сравнении величины остаточной дисперсии, рассчитанный при разных моделях. Графический метод достаточно нагляден и основан на поле корреляции.
может быть осуществлен тремя методами: графическим; аналитическим; экспериментальным. Аналитический метод основан на изучении материальной природы связи исследуемых признаков. Экспериментальный метод основан на сравнении величины остаточной дисперсии, рассчитанный при разных моделях. Графический метод достаточно нагляден и основан на поле корреляции.
Построение уравнения регрессии сводится к оценке ее параметров.
Для оценки параметров регрессии, линейных по параметрам, используют метод наименьших квадратов (МНК). МНК позволяет получить такие оценки параметров, при которых сумма квадратов отклонений фактических значений результативного признака  от теоретических
от теоретических  минимальна, т.е.
минимальна, т.е. 
Получаем следующую систему нормальных уравнений для оценки параметров а и  :
:  решая которую либо методом последовательного исключения переменных, либо методом определителей, находят искомые оценки параметров а и
решая которую либо методом последовательного исключения переменных, либо методом определителей, находят искомые оценки параметров а и  . Можно воспользоваться следующими готовыми формулами:
. Можно воспользоваться следующими готовыми формулами:  ;
;  , где
, где  - ковариация признаков,
- ковариация признаков,  - дисперсия признака х,
- дисперсия признака х, 

Параметр  называется коэффициентом регрессии. Его величина показывает среднее изменение результата с изменением фактора на одну единицу. Параметр a может не иметь экономического содержания. Интерпретировать можно лишь знак при параметре а. Если а>0, то относительное изменение результата происходит медленнее, чем изменение фактора.
называется коэффициентом регрессии. Его величина показывает среднее изменение результата с изменением фактора на одну единицу. Параметр a может не иметь экономического содержания. Интерпретировать можно лишь знак при параметре а. Если а>0, то относительное изменение результата происходит медленнее, чем изменение фактора.
Тесноту связи изучаемых явлений оценивает линейный коэффициент парной корреляции  для линейной регрессии
для линейной регрессии 
 , причем
, причем 
Для оценки качества подбора функции рассчитывается квадрат коэффициента корреляции, называемый коэффициентом детерминации. Коэффициент детерминации характеризует долю дисперсии результативного признака у, объясняемую регрессией, в общей дисперсии результативного признака:
 .
.
Коэффициент эластичности определяется по формуле  первая производная, характеризующая соотношение приростов результата и фактора для соответствующей формы связи. Средний коэффициент эластичности
первая производная, характеризующая соотношение приростов результата и фактора для соответствующей формы связи. Средний коэффициент эластичности  показывает, на сколько процентов в среднем по совокупности изменится результат у от своей средней величины при изменении фактора х на 1% от своего среднего значения.
показывает, на сколько процентов в среднем по совокупности изменится результат у от своей средней величины при изменении фактора х на 1% от своего среднего значения.
Средняя ошибка аппроксимации – среднее отклонение расчетных значений  от фактических у:
от фактических у:

 - относительная ошибка аппроксимации. Возможно и иное определение средней ошибки аппроксимации:
- относительная ошибка аппроксимации. Возможно и иное определение средней ошибки аппроксимации:  Ошибка аппроксимации в пределах 5 – 7% свидетельствует о хорошем подборе модели к исходным данным. Допустимый предел значений
Ошибка аппроксимации в пределах 5 – 7% свидетельствует о хорошем подборе модели к исходным данным. Допустимый предел значений  - не более 8 – 10%.
- не более 8 – 10%.
Оценка значимости уравнения регрессии в целом дается с помощью F – критерии Фишера. При этом выдвигается нулевая гипотеза Н0 о статистической незначимости уравнения регрессии и показателя тесноты связи и выполняется сравнение фактического Fфакт и критического (табличного) Fтабл значений F – критерия Фишера.
Непосредственному расчету F– критерия предшествует анализ дисперсии. Центральное место в нем занимает разложение общей суммы квадратов отклонений переменной у от среднего значения 
 на две части – “объясненную” (или “факторную”, т.е.
на две части – “объясненную” (или “факторную”, т.е.  ) и “необъясненную” (или остаточную, т.е.
) и “необъясненную” (или остаточную, т.е.  ):
):  .
.
Любая сумма квадратов отклонений связана с числом степеней свободы, т.е. c числом свободы независимого варьирования признака: n-1=m+(n-m-1), где n – число наблюдений, m – число параметров при переменных х.
Разделив каждую сумму квадратов на соответствующее ей число степеней свободы, получим средний квадрат отклонений, или, что то же самое, дисперсию на одну степень свободы D.
Dобщ=  ; Dфакт=
; Dфакт=  ; Dост=
; Dост=  .
.
Сопоставляя факторную и остаточную дисперсии в расчете на одну степень свободы, получим F критерий: Fфакт=  или Fфакт=
или Fфакт= 
Табличное значение F – критерия – это максимально возможное значение критерия под влиянием случайных факторов при уровне значимости 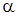 и данных степенях свободы (k1=m; k2=n-m-1). Уровень значимости
и данных степенях свободы (k1=m; k2=n-m-1). Уровень значимости 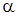 - вероятность отвергнуть правильную гипотезу при условии, что она верна (обычно
- вероятность отвергнуть правильную гипотезу при условии, что она верна (обычно 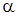 =0,05 или
=0,05 или 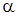 =0,01).
=0,01).
Если Fфакт> Fтабл , то Н0 – гипотеза о случайной природе оцениваемых характеристик отклоняется и признается их статистическая значимость . Если Fфакт<Fтабл , то гипотеза Н0 не отклоняется и признается статистическая незначимость уравнения регрессии.
Оценка значимости уравнения регрессии обычно дается в виде таблицы дисперсионного анализа (табл.1)
Таблица 1
| Источники вариации | Число степеней свободы | Сумма квадратов отклонений | Дисперсия на одну степень свободы | F – отношение | |
| фактическое | Табличное при 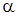 =… =…
| ||||
| Общая | n-1 | 
| Dобщ= 
| ||
| Объясненная (факторная) | m | 
| Dфакт= 
| Fфакт= 
| Fтабл=
F( 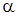 ;m;n-m-1) ;m;n-m-1)
|
| Остаточная | n-m-1 | 
| Dост= 
|
Для оценки статистической значимости коэффициентов регрессии и корреляции рассчитываются t критерии Стьюдента и доверительные интервалы каждого из показателей. Выдвигается гипотеза Н0 о случайной природе показателей, т.е. о незначимом их отличии от нуля. Оценка значимости коэффициентов регрессии и корреляции с помощью t – критерия Стьюдента проводится путем сопоставления их значений с величиной случайной ошибки: 
Случайные ошибки параметров регрессии и коэффициента корреляции определяются по формулам:

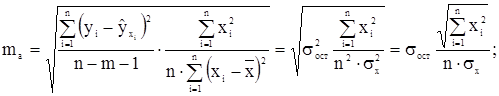
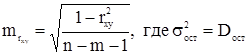 - остаточная дисперсия на одну степень свободы:
- остаточная дисперсия на одну степень свободы:  .
.
Между F критерием Фишера и t статистикой Стьюдента существует связь, которую можно выразить равенством  .
.
Критическое (табличное) значение t статистики определяется уровнем значимости 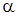 и числом степеней свободы d.f.=n-m-1,т.е. tтабл=t(
и числом степеней свободы d.f.=n-m-1,т.е. tтабл=t( 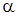 ;n-m-1)
;n-m-1)
Если tфакт> tтабл, то Н0 отклоняется, т.е. a,b,rxy не случайно отличаются от нуля и сформировались под влиянием систематически действующего фактора x. Если tфакт< tтабл, то Н0 не отклоняется и признается случайная природа формирования a,b,rxy
Для расчета доверительного интервала определяем предельную ошибку  для каждого показателя:
для каждого показателя:  и границы доверительных интервалов имеют вид:
и границы доверительных интервалов имеют вид: 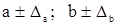 .
.
Если в доверительный интервал попадает ноль (т.е. нижняя граница отрицательна, а верхняя положительна), то оцениваемый параметр принимается нулевым, так как он не может одновременно принимать и положительное, и отрицательное значения.
Прогнозное значение  определяется путем подстановки в уравнение регрессии соответствующего прогнозного значения
определяется путем подстановки в уравнение регрессии соответствующего прогнозного значения  . Вычисляется средняя стандартная ошибка прогноза:
. Вычисляется средняя стандартная ошибка прогноза:
 и строится доверительный интервал прогноза, границы которого определяются как
и строится доверительный интервал прогноза, границы которого определяются как  предельная ошибка прогноза.
предельная ошибка прогноза.
Постановка задачи
По территориям региона приводятся данные за 199Х год (табл.2).
Таблица 2
| № региона | Среднедушевой прожиточный минимум в день , руб.,x | Среднедневная заработная плата , руб., y |
Продолжение таблицы 2
Требуется:
1. Построить поле корреляции.
2. Для характеристики зависимости у от х:
а) построить линейное уравнение парной регрессии у от х;
б) оценить тесноту связи с помощью коэффициентов корреляции и детерминации;
в) оценить качество линейного уравнения с помощью средней ошибки аппроксимации;
г) дать оценку силы связи с помощью среднего коэффициента эластичности;
д) оценить статистическую значимость результатов регрессионного моделирования с помощью F – критерия Фишера.
е) оценить статистическую значимость параметров регрессии и корреляции,
ж) найти прогнозное значение результата, если прогнозное значение фактора увеличится на 5% от среднего уровня . Определить доверительный интервал прогноза при уровне значимости 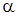 =0,05 .
=0,05 .
3. Проверить полученные результаты с помощью ППП МS Excel.
|
из
5.00
|
Обсуждение в статье: Теоретические сведения. Лабораторная работа №1 |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

