 |
Главная |
Теоретические сведения. Множественная регрессия – уравнение связи с несколькими независимыми переменными:
|
из
5.00
|
Множественная регрессия – уравнение связи с несколькими независимыми переменными:  , где у – зависимая переменная (результативный признак);
, где у – зависимая переменная (результативный признак);  - независимые переменные (факторы).
- независимые переменные (факторы).
Для построения уравнения множественной регрессии чаще используют следующие функции:
- линейная - 
- степенная -  ;
;
- экспонента -  ;
;
- гипербола -  .
.
Для оценки параметров уравнения множественной регрессии применяют МНК. Для линейных уравнений и нелинейных уравнений, приводимых к линейным, строится следующая система нормальных уравнений, решение которой позволяет получить оценки параметров регрессии:

Для ее решения может быть применен метод определителей: 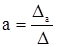 ;
;  ; …;
; …; 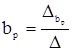 , где
, где  определитель системы,
определитель системы,  а,
а,  b
b  ;…;
;…;  – частные определители, которые получаются путем замены соответствующего столбца матрицы определителя системы данными левой части системы.
– частные определители, которые получаются путем замены соответствующего столбца матрицы определителя системы данными левой части системы.
Другой вид уравнения множественной регрессии – уравнение регрессии в стандартизованном масштабе: ty=  , где
, где  стандартизованные переменные;
стандартизованные переменные;  - стандартизованные коэффициенты регрессии.
- стандартизованные коэффициенты регрессии.
К уравнению множественной регрессии в стандартизованном масштабе применим МНК. Стандартизованные коэффициенты регрессии (  - коэффициенты) определяются из следующей системы уравнений:
- коэффициенты) определяются из следующей системы уравнений:

где  парные коэффициенты корреляции результата с каждым фактором,
парные коэффициенты корреляции результата с каждым фактором,  - коэффициенты межфакторной корреляции.
- коэффициенты межфакторной корреляции.
Связь коэффициентов множественной регрессии bi со стандартизованными коэффициентами  описывается соотношением bi =
описывается соотношением bi = 
 .
.
Параметр aопределяется как  .
.
Коэффициенты «чистой» регрессии bi несравнимы между собой. В силу того, что все переменные заданы как центрированные и нормированные, стандартизованные коэффициенты регрессии  сравнимы между собой. Сравнивая их друг с другом, можно ранжировать факторы по силе их воздействия на результат.
сравнимы между собой. Сравнивая их друг с другом, можно ранжировать факторы по силе их воздействия на результат.
Средние по совокупности коэффициенты эластичности для линейной множественной регрессии рассчитываются по формуле  , при этом воздействие остальных факторов считается неизменным.
, при этом воздействие остальных факторов считается неизменным.
Для расчета частных коэффициентов эластичности применяется следующая формула  , где
, где  частное уравнение регрессии, т.е. уравнение регрессии, которое связывает результативный признак y с фактором xi при закреплении факторов x1, x2,…, xi-1, xi+1,…,xp на среднем уровне.
частное уравнение регрессии, т.е. уравнение регрессии, которое связывает результативный признак y с фактором xi при закреплении факторов x1, x2,…, xi-1, xi+1,…,xp на среднем уровне.
Тесноту совместного влияния факторов на результат оценивает индекс множественной корреляции  , причем
, причем  и
и 
 (i=1,…,p).
(i=1,…,p).
Для уравнения в стандартизованном масштабе  . При линейной зависимости R
. При линейной зависимости R  =
=  , где
, где  определитель матрицы парных коэффициентов корреляции,
определитель матрицы парных коэффициентов корреляции,  определитель матрицы межфакторной корреляции, т.е.
определитель матрицы межфакторной корреляции, т.е.


Частные коэффициенты (или индексы) корреляции, измеряющие влияние на у фактора хi при неизменном уровне других факторов можно определить по формулам: r  или
или
r  =
=  .
.
Частные коэффициенты корреляции изменяются в пределах от –1 до 1.
Качество построенной модели в целом оценивает коэффициент (индекс) детерминации, который рассчитывается как квадрат индекса множественной корреляции:  . Скорректированный индекс множественной детерминации содержит поправку на число степеней свободы и рассчитывается по формуле
. Скорректированный индекс множественной детерминации содержит поправку на число степеней свободы и рассчитывается по формуле  , где n число наблюдений, m число факторов.
, где n число наблюдений, m число факторов.
Средняя ошибка аппроксимации и оценка значимости уравнения множественной регрессии в целом определяется аналогично парной регрессии и корреляции.
Частный F – критерий оценивает статистическую значимость присутствия каждого из факторов в уравнении. В общем виде фактическое значение частного F критерия для фактора xi определится как  .
.
Фактическое значение частного F-критерия сравнивается с табличным Fтабл = F ( 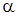 ;1; n – m – 1). Если
;1; n – m – 1). Если  , то дополнительное включение фактора xi в модель статистически оправданно и коэффициент чистой регрессии bi при факторе xi статистически значим. Если
, то дополнительное включение фактора xi в модель статистически оправданно и коэффициент чистой регрессии bi при факторе xi статистически значим. Если  , то нецелесообразно включение фактора xi в модель.
, то нецелесообразно включение фактора xi в модель.
Оценка значимости коэффициентов чистой регрессии с помощью t – критерия Стьюдента производится аналогично парной регрессии и корреляции, причем справедливо соотношение  , а также
, а также  , где
, где 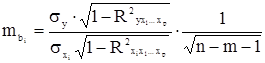 средняя квадратическая ошибка коэффициента регрессии bi.
средняя квадратическая ошибка коэффициента регрессии bi.
Постановка задачи
По 20 предприятиям региона (табл. 9) изучается зависимость выработки продукции на одного работника у (тыс. руб.) от ввода в действие новых основных фондов х1 (% от стоимости фондов на конец года) и от удельного веса рабочих высокой квалификации в общей численности рабочих х2 (%).
Таблица 9
| Номер предприятия | y | х1 | x2 | Номер предприятия | у | x1 | x2 |
| 7,0 | 3,9 | 10,0 | 9,0 | 6,0 | 21,0 | ||
| 7,0 | 3,9 | 14,0 | 11,0 | 6,4 | 22,0 | ||
| 7,0 | 3,7 | 15,0 | 9,0 | 6,8 | 22,0 | ||
| 7,0 | 4,0 | 16,0 | 11,0 | 7,2 | 25,0 | ||
| 7,0 | 3,8 | 17,0 | 12,0 | 8,0 | 28,0 | ||
| 7,0 | 4,8 | 19,0 | 12,0 | 8,2 | 29,0 | ||
| 8,0 | 5,4 | 19,0 | 12,0 | 8,1 | 30,0 | ||
| 8,0 | 4,4 | 20,0 | 12,0 | 8,5 | 31,0 | ||
| 8,0 | 5,3 | 20,0 | 14,0 | 9,6 | 32,0 | ||
| 10,0 | 6,8 | 20,0 | 14,0 | 9,0 | 36,0 |
Требуется:
1. Оценить показатели вариации каждого признака и сделать вывод о возможностях применения МНК для их изучения.
|
из
5.00
|
Обсуждение в статье: Теоретические сведения. Множественная регрессия – уравнение связи с несколькими независимыми переменными: |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

