Проверка качества уравнения регрессии

Регрессионный анализ позволяет определить оценки коэффициентов регрессии. Но они не позволяют сдеалть вывод, насколько точно эмпирическое уравнение регресси соответствует уравнению для всей генеральной совокупности, насколько близки оценк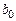и и 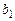коэффициентов к своим теоретическим прототипам 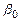и 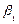, как близко оцененное значение 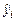к условному математическому ожиданию 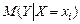, насколько надежны найденные оценки. Для ответа на эти вопросы необходимы дополнительные исследования.

Как следует из соотношения (1.6), значения 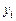зависят от значений 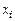и случайных отклонений . Следовательно, переменная 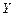является случайной величиной, напрямую связанной с . Таким образом, пока не будет определенности в вероятностном поведении , нет уверенности в качестве оценок.

Доказано, что для получения по МНК наилучших результатов необходимо, чтобы выполнялся ряд предпосылок относительно случайного отклонения (предпосылки Гаусса-Маркова):

1. Математическое ожидание случайного отклонения равно нулю: 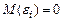для всех наблюдений. Данное условие означает, что случайное отклонение в среднем не оказывает влияния на зависимую переменную. В каждом конкретном наблюдении может быть либо положительным, либо отрицательным, но он не должен иметь систематического смещения. Выполнимость влечет выполнимость

2. Дисперсия случайных отклонений постоянна: для любых наблюдений i и j. Данное условие подразумевает, что несмотря на то, что при каждом конкретном наблюдении случайное отклонение может быть либо большим, либо меньшим, не должно быть некой причины, вызывающей большую ошибку (отклонение).

3. Случайные отклонения и являются независимыми друг от друга для . Выполнимость данной предпосылки предполагает, что отсутствует систематическая связь между любыми случайными отклонениями.

4. Случайное отклонение должно быть независимо от объясняющих переменных.

5. Модель является линейной относительно параметров.

Теорема Гаусса-Маркова. Если предпосылки 1-5 выполнены, то оценки, полученные по МНК, обладают следующими свойствами:

1. Оценки являются несмещенными, т.е. 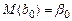, . Это вытекает из того, что 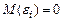, и говорит об отсутствии систематической ошибки в определении положения линии регрессии.

2. Оценки состоятельны, так как дисперсия оценок параметров при возрастании числа наблюдений стремится к нулю: , . Другими словами, при увеличении объема выборки надежность оценок увеличивается ( 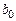близко к 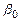, а 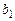близко к .

3. Оценки эффективны, т.е. они имеют наименьшую дисперсию по сравнению с любыми другими оценками данных параметров, линейными относительно величин .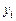

Если предпосылки 2 и 3 нарушены, то свойства несмещенности и состоятельности сохраняются, но свойство эффективности – нет.