 |
Главная |
Дисперсии отклонений неизвестны
|
из
5.00
|
Для применения ВМНК необходимо знать фактические значения дисперсий  . На практике такие значения известны очень редко. Следовательно, чтобы применить ВМНК, необходимо сделать реалистические предположения о значениях
. На практике такие значения известны очень редко. Следовательно, чтобы применить ВМНК, необходимо сделать реалистические предположения о значениях  .
.
- Может оказаться целесообразным предположить, что дисперсии  отклонений
отклонений  пропорциональны значениям
пропорциональны значениям 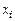 , что отражено на рисунке 4.3.
, что отражено на рисунке 4.3.
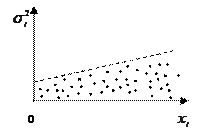
Рис. 4.3
В этом случае  (
(  – коэффициент пропорциональности). Тогда уравнение (4.5) преобразуется делением его левой и правой части на
– коэффициент пропорциональности). Тогда уравнение (4.5) преобразуется делением его левой и правой части на  :
:
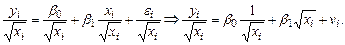 (4.8)
(4.8)
При этом для случайных отклонений  выполняется условие гомоскедастичности. Оценив для (4.8) коэффициенты
выполняется условие гомоскедастичности. Оценив для (4.8) коэффициенты 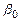 и
и  , затем возвращаются к исходному уравнению регрессии (4.5).
, затем возвращаются к исходному уравнению регрессии (4.5).
Если в уравнении регрессии присутствуют несколько объясняющих переменных, можно поступить следующим образом. Вместо конкретной объясняющей переменной  используются значения, рассчитанные по эмпирическому уравнению регрессии:
используются значения, рассчитанные по эмпирическому уравнению регрессии:  . В этом случае получают следующую регрессию:
. В этом случае получают следующую регрессию:
 (4.9)
(4.9)
- Можно сделать предположение о том, что дисперсии  отклонений
отклонений  пропорциональны значениям
пропорциональны значениям  , что отражено на рисунке 4.4.
, что отражено на рисунке 4.4.
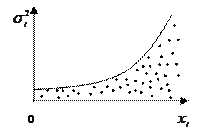
Рис. 4.4
В этом случае необходимо преобразовать (4.5) делением на 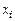 к виду:
к виду:
 . (4.10)
. (4.10)
При этом для случайных отклонений  выполняется условие гомоскедастичности. Оценив для (4.10) коэффициенты
выполняется условие гомоскедастичности. Оценив для (4.10) коэффициенты 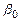 и
и  , затем возвращаются к исходному уравнению регрессии (4.5).
, затем возвращаются к исходному уравнению регрессии (4.5).
Для применения описанных выше методов весьма значимы знания об истинных значениях дисперсий отклонений  , либо предположения, какими эти дисперсии могут быть. На практике рекомендуется применять несколько методов определения гетероскедастичности и способов ее корректировки.
, либо предположения, какими эти дисперсии могут быть. На практике рекомендуется применять несколько методов определения гетероскедастичности и способов ее корректировки.
Пример.Исследуем зависимость между доходом (Х) домохозяйства и его расходом (Y) на продукты питания. Выборочные данные по 40 домохозяйствам представлены в таблице 4.1.
Таблица 4.1
| X | Y | X | Y | X | Y | X | Y | |||
| 25,5 | 14,5 | 42,5 | 14,9 | 61,0 | 10,9 | 79,2 | 19,8 | |||
| 26,5 | 11,3 | 44,2 | 11,6 | 61,7 | 16,1 | 81,5 | 21,2 | |||
| 27,2 | 14,7 | 44,8 | 21,5 | 62,5 | 10,5 | 82,4 | 29,0 | |||
| 29,6 | 10,2 | 45,5 | 10,8 | 64,7 | 10,6 | 82,8 | 17,3 | |||
| 35,7 | 13,5 | 45,5 | 13,8 | 69,7 | 29,0 | 83,0 | 23,5 | |||
| 38,6 | 9,9 | 48,3 | 16,0 | 71,2 | 8,2 | 85,9 | 22,0 | |||
| 39,0 | 12,4 | 49,5 | 18,2 | 73,8 | 14,3 | 86,4 | 18,3 | |||
| 39,3 | 8,6 | 52,3 | 19,1 | 74,7 | 21,8 | 86,9 | 13,7 | |||
| 40,0 | 10,3 | 55,7 | 16,3 | 75,8 | 26,1 | 88,3 | 14,5 | |||
| 41,9 | 13,9 | 59,0 | 17,5 | 76,9 | 20,0 | 89,0 | 27,3 |
Построим эмпирическое уравнение регрессии и проведем анализ модели на наличие гетероскедастичности.
По (1.11) определим коэффициенты эмпирического уравнения регрессии:  ,
, 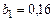 . Следовательно, уравнение имеет вид:
. Следовательно, уравнение имеет вид:  .
.
Определим отклонения  (где
(где  ),
),  , ранги
, ранги 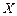 и
и  . Рассчитанные величины представим в таблице 4.2.
. Рассчитанные величины представим в таблице 4.2.
Таблица 4.2
| X | Y | 
| 
| 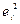
| Ранг Х | Ранг  (абсол. вел.) (абсол. вел.)
| 
| 
| ||
| 25,5 | 14,5 | 11,120 | 3,380 | 11,4244 | -33 | |||||
| 26,5 | 11,3 | 11,280 | 0,020 | 0,0004 | -17 | |||||
| 27,2 | 14,7 | 11,392 | 3,308 | 10,9429 | -30 | |||||
| 29,6 | 10,2 | 11,776 | -1,576 | 2,4838 | -11 | |||||
| 35,7 | 13,5 | 12,752 | 0,748 | 0,5595 | -19 | |||||
| 38,6 | 9,9 | 13,216 | -3,316 | 10,9959 | -4 | |||||
| 39,0 | 12,4 | 13,280 | -0,880 | 0,7744 | -9 | |||||
| 39,3 | 8,6 | 13,328 | -4,728 | 22,3540 | ||||||
| 40,0 | 10,3 | 13,440 | -3,140 | 9,8596 | -2 | |||||
| 41,9 | 13,9 | 13,744 | 0,156 | 0,0243 | -11 | |||||
| 42,5 | 14,9 | 13,840 | 1,060 | 1,1236 | -15 | |||||
| 44,2 | 11,6 | 14,112 | -2,512 | 6,3101 | -2 | |||||
| 44,8 | 21,5 | 14,208 | 7,292 | 53,1733 | -25 | |||||
| 45,5 | 10,8 | 14,320 | -3,520 | 12,3904 | ||||||
| 45,5 | 13,8 | 14,320 | -0,520 | 0,2704 | -4 | |||||
| 48,3 | 16,0 | 14,768 | 1,232 | 1,5178 | -13 | |||||
| 49,5 | 18,2 | 14,960 | 3,240 | 10,4976 | -15 | |||||
| 52,3 | 19,1 | 15,408 | 3,692 | 13,6309 | -17 | |||||
| 55,7 | 16,3 | 15,952 | 0,348 | 0,1211 | -3 | |||||
| 59,0 | 17,5 | 16,480 | 1,020 | 1,0404 | -5 | |||||
| 61,0 | 10,9 | 16,800 | -5,900 | 34,8100 | ||||||
| 61,7 | 16,1 | 16,912 | -0,812 | 0,6593 | ||||||
| 62,5 | 10,5 | 17,040 | -6,540 | 42,7716 | ||||||
| 64,7 | 10,6 | 17,392 | -6,792 | 46,1313 | ||||||
| 69,7 | 29,0 | 18,192 | 10,808 | 116,8129 | -15 | |||||
| 71,2 | 8,2 | 18,432 | -10,232 | 104,6938 | ||||||
| 73,8 | 14,3 | 18,848 | -4,548 | 20,6843 | ||||||
| 74,7 | 21,8 | 18,992 | 2,808 | 7,8849 | -2 | |||||
| 75,8 | 26,1 | 19,168 | 6,932 | 48,0526 | -8 | |||||
| 76,9 | 20,0 | 19,344 | 0,656 | 0,4303 | ||||||
| 79,2 | 19,8 | 19,712 | 0,088 | 0,0077 | ||||||
| 81,5 | 21,2 | 20,080 | 1,120 | 1,2544 | ||||||
| 82,4 | 29,0 | 20,224 | 8,776 | 77,0182 | -6 | |||||
| 82,8 | 17,3 | 20,288 | -2,988 | 8,9281 | ||||||
| 83,0 | 23,5 | 20,320 | 3,180 | 10,1124 | ||||||
| 85,9 | 22,0 | 20,784 | 1,216 | 1,4787 | ||||||
| 86,4 | 18,3 | 20,864 | -2,564 | 6,5741 | ||||||
| 86,9 | 13,7 | 20,944 | -7,244 | 52,4755 | ||||||
| 14,5 | 21,168 | -6,668 | 44,4622 | ||||||
| 89,0 | 27,3 | 21,280 | 6,020 | 36,2404 |
 Проанализируем графически остатки, представив зависимость
Проанализируем графически остатки, представив зависимость  от
от 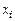 (рис. 4.5).
(рис. 4.5).
Рис. 4.5
Изучая график, можно обнаружить, что с увеличением 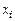 возрастает разброс значений
возрастает разброс значений  , что свидетельствует о наличии гетероскедастичности.
, что свидетельствует о наличии гетероскедастичности.
Применим для обнаружения гетероскедастичности тест ранговой корреляции Спирмена. Для этого рассчитаем по (4.1) коэффициент ранговой корреляции:

Рассчитаем  -статистику:
-статистику:
 .
.
Из приложения 1 определим критическое значение  -статистики для числа степеней свободы
-статистики для числа степеней свободы  и уровня значимости
и уровня значимости  :
:  . Так как рассчитанное значение
. Так как рассчитанное значение  -статистики превышает критическое, определенное по приложению 1, то гипотеза об отсутствии гетероскедастичности отклоняется с уровнем значимости
-статистики превышает критическое, определенное по приложению 1, то гипотеза об отсутствии гетероскедастичности отклоняется с уровнем значимости  .
.
Проверим гипотезу об отсутствии гетероскедастичности с помощью теста Голдфелда-Квандта. Для этого разобьем ряд на три подвыборки размерности 14, 12, 14.
Определим дисперсии отклонений для первой и третьей подвыборок:
 и
и  .
.
Определим значение  -статистики.
-статистики. 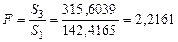 .
.
Из приложения 2 определим критическое значение  -статистики для числа степеней свободы
-статистики для числа степеней свободы  и уровня значимости
и уровня значимости  :
:  . Так как рассчитанное значение
. Так как рассчитанное значение  -статистики превышает критическое, определенное по приложению 2, то гипотеза об отсутствии гетероскедастичности отклоняется с уровнем значимости
-статистики превышает критическое, определенное по приложению 2, то гипотеза об отсутствии гетероскедастичности отклоняется с уровнем значимости  .
.
Следовательно, по всем трем тестам гетероскедастичность в данной модели присутствует.
Автокорреляция
|
из
5.00
|
Обсуждение в статье: Дисперсии отклонений неизвестны |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

