Логарифмические (лог-линейные) модели

 

Рассмотрим модель парной регрессии. Пусть некоторая экономическая зависимость моделируется формулой:

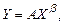(3.1)

где – параметры модели (константы, подлежащие определению).

Это функция может отражать зависимость спроса 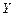на благо от его цены 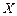(тогда 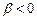); зависимость спроса 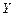на благо от дохода 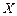(тогда ); зависимость объема выпуска 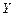от использования ресурса 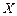(тогда ).

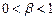Для анализа функций вида (3.1) используется логарифмирование по экспоненте. Прологарифмировав обе части, имеем:

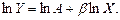(3.2)

Заменим 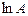на :

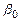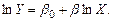(3.3)

С целью статистической оценки коэффициентов добавим в модель случайную погрешность , в результате получим двойную логарифмическую модель (и зависимая переменная, и объясняющая переменная заданы в логарифмическом виде):

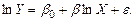(3.4)

Введем замены 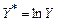и 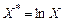, получаем:

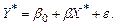(3.5)

Модель (3.5) является линейной моделью, подробно рассмотренной ранее. Коэффициент определяет эластичность переменной 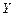по переменной 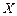, т.е. процентное изменение 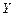для данного процентного изменения 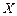. Действительно, продифференцировав обе части (3.4), получаем:

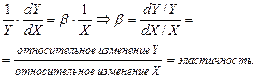
В случае парной регрессии обоснованность использования логарифмической модели проверить достаточно просто. Для этого определяются точки 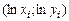, , 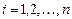которые затем наносятся на корреляционное поле. Если их расположение соответствует прямой линии, то использование данной модели обоснованно.

При большем числе переменных:

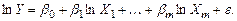(3.6)

Коэффициенты являются эластичностями переменной 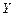по переменной .

 

Полулогарифмические модели

Полулогарифмическими моделями являются модели вида (в случае парной регрессии):

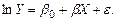(3.7)

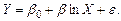(3.8)

Лог-линейная модель

Рассмотрим известную в банковском анализе зависимость:

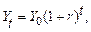(3.9)

где 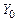– первоначальный вклад в банке; – процентная ставка; 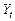– вклад в банке в момент времени .

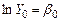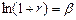Прологарифмировав обе части (3.9): и введя обозначение , , а также введя случайное слагаемое 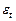, получаем модель вида (3.7):

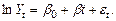
Полулогарифмическая модель (3.7) легко сводится к линейной модели путем замены 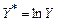, т.е. .

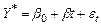Коэффициент в (3.7) имеет смысл темпа прироста переменной 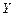по переменной 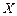. Действительно, продифференцировав обе части (3.7), получаем:

 

Линейно-логарифмическая модель

Линейно-логарифмическая модель (3.8) сводится к линейной модели путем замены: 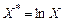, т.е.:

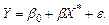(3.10)

Коэффициент в (3.8) определяет изменение переменной 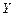вследствие единичного относительного прироста 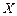. Действительно, продифференцировав обе части (3.8), получаем:

 

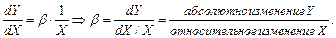
Обратная модель

 

Обратной моделью называется модель вида:

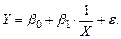(3.11)

Она сводится к линейной путем замены: 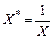. Таким образом:

(3.12)

В зависимости от знаков возможны случаи, представленные на рис. 3.1.

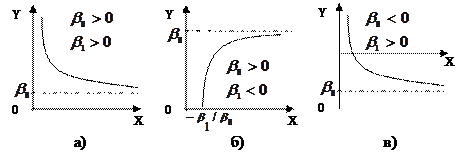
Рис. 3.1

 

График рис. 3.1, а может отражать зависимость между объемом выпуска 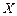и средними фиксированными издержками 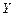. График рис. 3.1, б может отражать зависимость между доходом 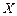и спросом на блага 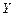. График рис. 3.1, в может отражать зависимость между уровнем безработицы 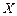в процентах и процентным изменением заработной платы (кривая Филлипса).

 

Показательная модель

 

Показательная функция имеет вид:

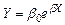(3.13)

и сводится к лог-линейной модели путем логарифмирования:

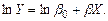(3.14)

Сведение лог-линейной модели к линейной рассмотрено в главе 3.2.

 

Выбор формы модели

 

Многообразие и сложность экономических процессов предопределяют многообразие моделей, используемых для экономического анализа. Это существенно усложняет процесс нахождения максимально адекватной формулы зависимости. Для случая парной регрессии подбор модели обычно осуществляется на основе расположения наблюдаемых точек на корреляционном поле. Однако нередки ситуации, когда расположение точек приблизительно соответствует нескольким функциям и необходимо из них выявить наилучшую.

На практике неизвестно, какая модель является верной, и зачастую подбирают такую модель, которая наиболее точно соответствует реальным данным. Признаками «хорошей» модели являются:

1. Скупость (простота). Модель должна быть максимально простой. Данное свойство определяется тем фактом, что модель не отражает действительность идеально, а является ее упрощением. Поэтому из двух моделей, приблизительно одинаково отражающих реальность, предпочтение отдается модели, содержащей меньшее число объясняющих переменных.

2. Единственность. Для любого набора статистических данных определяемые коэффициенты должны вычисляться однозначно.

3. Максимально соответствие. Уравнение тем лучше, чем большую часть разброса зависимой переменной оно может объяснить. Поэтому стремятся построить уравнение с максимально возможным скорректированным коэффициентом детерминации .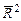

4. Согласованность с теорией. Никакое уравнение не может быть признано качественным, если оно не соответствует известным теоретическим предпосылкам.

5. Прогнозные качества. Модель может быть признана качественной, если полученные на ее основе прогнозы подтверждаются реальностью. Другим критерием прогнозных качеств оцененной модели регрессии может служить следующее отношение:

, (3.15)

где 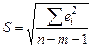– стандартная ошибка регрессии, 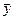– среднее значение зависимой переменной. Если мала (она определяет относительную ошибку прогноза в процентах) и отсутствует автокорреляция остатков, то прогнозные качества модели высоки.

Пример. Анализируется индекс потребительских цен 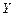по объему денежной массы 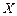на основании приведенных в таблице 3.1 данных. Необходимо построить логарифмическую модель.

Таблица 3.1

Год			Год
	72,5			106,5
	77,5
				115,5
	85,5			118,5
	88,5
				120,5

 

Решение.

Логарифмическая модель имеет вид: . Данная модель сводится к линейной следующим образом: 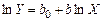(глава 3.1). Для определения коэффициентов в этой модели определим логарифмы переменных 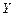и 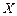, , 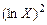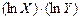и представим их в таблице 3.2.

 

Таблица 3.2

Год
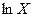
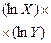
			4,1744	4,7005	22,0947	19,6218
			4,2195	4,8283	23,3125	20,3730
	72,5		4,2836	4,8828	23,8417	20,9160
	77,5		4,3503	4,9200	24,2064	21,4035
			4,4067	5,0752	25,7577	22,3649
	85,5		4,4485	5,1761	26,7920	23,0259
	88,5		4,4830	5,2575	27,6413	23,5694
			4,5109	5,3706	28,8433	24,2262
			4,5539	5,4596	29,8072	24,8625
			4,6052	5,4806	30,0370	25,2393
	106,5		4,6681	5,5013	30,2643	25,6806
Продолжение табл. 3.2 92			4,7185	5,5215	30,4870	26,0532
	115,5		4,7493	5,6168	31,5484	26,6759
	118,5		4,7749	5,6525	31,9508	26,9901
			4,7875	5,6870	32,3420	27,2265
	120,5		4,7916	5,7683	33,2733	27,6394
			4,7958	5,8406	34,1126	28,0103
Сумма			77,3217	90,7392	486,3122	413,8784
Среднее	96,4118	219,8235	4,5483	5,3376	28,6066	24,3458

 

Затем, по аналогии с примером, приведенным в главе 1, рассчитываются коэффициенты для этой модели следующим образом:

 

Следовательно, модель имеет вид: 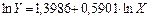. Если свести данную модель к виду , то получим:

 

(т.к. , следовательно, ).

 

Представим графически корреляционное поле для переменных и 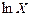, а также график рассчитанной модели (рис. 3.2).

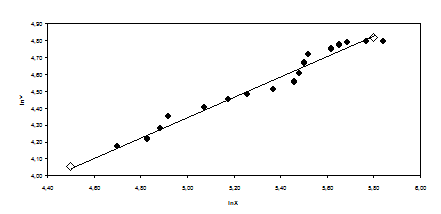Рис. 3.2

 

После определения коэффициентов модели необходимо проверить значимость коэффициентов уравнения регрессии, определить их интервальные оценки и рассчитать коэффициент детерминации. Расчет проводится аналогично примеру в главе 1 для модели вида .

 

 

Гетероскедастичность