 |
Главная |
Проверка выполнимости предпосылок МНК. Статистика Дарбина-Уотсона
|
из
5.00
|
Статистическая значимость коэффициентов регрессии и близкое к единице значение коэффициента детерминации  не гарантируют высокое качество уравнения регрессии. Поэтому следующим этапом проверки качества уравнения регрессии является проверка выполнимости предпосылок МНК. Причины и последствия невыполнимости этих предпосылок, методы корректировки регрессионных моделей будут рассмотрены в последующих главах. В данном параграфе рассмотрим популярную в регрессионном анализе статистику Дарбина-Уотсона.
не гарантируют высокое качество уравнения регрессии. Поэтому следующим этапом проверки качества уравнения регрессии является проверка выполнимости предпосылок МНК. Причины и последствия невыполнимости этих предпосылок, методы корректировки регрессионных моделей будут рассмотрены в последующих главах. В данном параграфе рассмотрим популярную в регрессионном анализе статистику Дарбина-Уотсона.
При статистическом анализе уравнения регрессии на начальном этапе часто проверяют выполнимость одной предпосылки: условия статистической независимости отклонений между собой. При этом проверяется некоррелированность соседних величин  (2.7).
(2.7).
Для анализа коррелированности отклонений используют статистику Дарбина-Уотсона:
 . (2.27)
. (2.27)
Критические значения  и
и 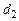 определяются на основе специальных таблиц (приложение 3) для требуемого уровня значимости
определяются на основе специальных таблиц (приложение 3) для требуемого уровня значимости  , числа наблюдений
, числа наблюдений  и количества объясняющих переменных
и количества объясняющих переменных  .
.
Выводы об отсутствии автокорреляции остатков осуществляются по следующей схеме (рис. 2.1).

 Рис. 2.1
Рис. 2.1
Не обращаясь к таблицам, можно пользоваться «грубым» правилом и считать, что автокорреляция остатков отсутствует, если 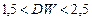 . Для более надежного вывода целесообразно обращаться к табличным значениям.
. Для более надежного вывода целесообразно обращаться к табличным значениям.
Пример.Анализируется объем  сбережений домохозяйства за 10 лет. Предполагается, что его размер
сбережений домохозяйства за 10 лет. Предполагается, что его размер 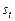 в текущем году
в текущем году  зависит от величины
зависит от величины  располагаемого дохода
располагаемого дохода 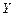 и от величины
и от величины  реальной процентной ставки
реальной процентной ставки  . Статистические данные представлены в таблице 2.1.
. Статистические данные представлены в таблице 2.1.
Таблица 2.1
| Год | |||||||||||
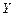 , тыс.у.е. , тыс.у.е.
 , % , %
 , тыс.у.е. , тыс.у.е.
|
Средние значения исходных данных равны:  ,
,  ,
,  .
.
Представим требующиеся для построения модели множественной регрессии и проведения дальнейшего анализа промежуточные вычисления в таблице 2.2.
Таблица 2.2
| Год | 
| 
| 
| 
| 
| 
|
| 5831,4050 | 1,8595 | 282,8512 | 104,1322 | 1284,2975 | 22,9339 | |
| 4404,1322 | 1,8595 | 139,6694 | 90,4959 | 784,2975 | 16,1157 | |
| 1322,3140 | 0,1322 | 46,4876 | 13,2231 | 247,9339 | 2,4793 | |
| 695,0413 | 1,8595 | 46,4876 | 35,9504 | 179,7521 | 9,2975 | |
| 267,7686 | 0,1322 | 3,3058 | 5,9504 | 29,7521 | 0,6612 | |
| 267,7686 | 0,4050 | 1,3967 | -10,4132 | -19,3388 | 0,7521 | |
| 13,2231 | 0,4050 | 10,1240 | 2,3140 | 11,5702 | 2,0248 | |
| 558,6777 | 0,1322 | 1,3967 | -8,5950 | 27,9339 | -0,4298 | |
| 2876,8595 | 0,4050 | 51,5785 | 34,1322 | 385,2066 | 4,5702 | |
| 5422,3140 | 2,6777 | 173,7603 | 120,4959 | 970,6612 | 21,5702 | |
| 6995,0413 | 2,6777 | 330,5785 | 136,8595 | 1520,6612 | 29,7521 | |

| 28654,5455 | 12,5455 | 1087,6364 | 524,5455 | 5422,7273 | 109,7273 |
Расчет коэффициентов уравнения регрессии производится по формулам (2.17):

Таким образом, эмпирическое уравнение регрессии имеет вид:

Подставляя соответствующие значения  и
и 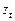 в эмпирическое уравнение регрессии, получаем
в эмпирическое уравнение регрессии, получаем 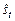 . Расчет отклонений
. Расчет отклонений  реальных значений от модельных представлен в таблице 2.3.
реальных значений от модельных представлен в таблице 2.3.
Таблица 2.3
| Год | 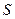
| 
| 
| 
| 
| 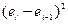
|
| 22,489 | -2,48873 | 6,19375 | - | - | ||
| 23,731 | 1,26939 | 1,61134 | 3,75811 | 14,1234 | ||
| 31,01 | -1,01008 | 1,02026 | -2,27947 | 5,19597 | ||
| 28,698 | 1,30183 | 1,69475 | 2,31191 | 5,34491 | ||
| 33,494 | 1,50614 | 2,26845 | 0,20431 | 0,04174 | ||
| 37,048 | 0,95234 | 0,90696 | -0,55380 | 0,30669 | ||
| 39,531 | 0,46856 | 0,21955 | -0,48378 | 0,23404 | ||
| 38,461 | -0,46142 | 0,21291 | -0,92998 | 0,86487 | ||
| 45,741 | -1,74089 | 3,03069 | -1,27947 | 1,63703 | ||
| 51,778 | -1,77846 | 3,16293 | -0,03758 | 0,00141 | ||
| 53,02 | 1,97965 | 3,91900 | 3,75811 | 14,1234 | ||
| сумма | 
| 24,24060 | 4,46837 | 41,8734 | ||
| 36,8182 | 36,8182 |
Рассчитаем дисперсию регрессии по формуле (2.19):
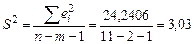 .
.
Определим дисперсии и стандартные ошибки коэффициентов по (2.20):
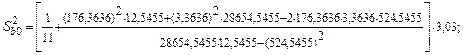
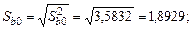




Рассчитаем по формуле (2.22) соответствующие  -статистики:
-статистики:
 ,
,  ,
, 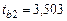 .
.
Проверим статистическую значимость коэффициентов на основе распределения Стьюдента. По таблице, приведенной в приложении 1, определим критические значения с уровнем значимости  :
:  . Таким образом,
. Таким образом,  ,
, 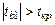 ,
,  .
.
По формуле (2.21) определим 95%-е интервальные оценки коэффициентов:
для 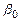 : (2,962233–2,306×1,8929; 2,962233+2,306×1,8929), т.е. (–1,4028; 7,3273);
: (2,962233–2,306×1,8929; 2,962233+2,306×1,8929), т.е. (–1,4028; 7,3273);
для  : (0,124189–2,306×0,0212; 0,124189+2,306×0,0212), т.е. (0,0753; 0,1731);
: (0,124189–2,306×0,0212; 0,124189+2,306×0,0212), т.е. (0,0753; 0,1731);
для 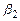 : (3,553796–2,306×1,0146; 3,553796+2,306×1,0146), т.е. (1,2141; 5,8935).
: (3,553796–2,306×1,0146; 3,553796+2,306×1,0146), т.е. (1,2141; 5,8935).
Рассчитаем коэффициент детерминации по формуле (2.23):
 .
.
Анализ статистической значимости коэффициента детерминации осуществляется на основе  -статистики (2.26):
-статистики (2.26):

Определим по приложению 2 критическую точку распределения Фишера:  с 95%-ой вероятностью. Очевидно, что 175,3722>4,46, следовательно, коэффициент детерминации статистически значим, т.е. совокупное влияние переменных
с 95%-ой вероятностью. Очевидно, что 175,3722>4,46, следовательно, коэффициент детерминации статистически значим, т.е. совокупное влияние переменных 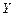 и
и  на переменную
на переменную  существенно.
существенно.
На основе проведенных рассуждений и вычислений можно заключить, что построенное уравнение регрессии объясняет 97,77% разброса зависимой переменной  . Однако для уверенности и обоснованности (чтобы исключить автокорреляцию) проведем исследование с помощью статистики Дарбина-Уотсона.
. Однако для уверенности и обоснованности (чтобы исключить автокорреляцию) проведем исследование с помощью статистики Дарбина-Уотсона.
Рассчитаем статистику по формуле (2.27):
 .
.
По приложению 3 определим критические точки для уровня значимости 0,05 и числа наблюдений 11:  .
.
Таким образом,  , т.е. (
, т.е. (  ), следовательно, имеются основания считать, что автокорреляция отсутствует. Это является одним из подтверждений высокого качества модели.
), следовательно, имеются основания считать, что автокорреляция отсутствует. Это является одним из подтверждений высокого качества модели.
По всем статистическим показателям модель может быть признана удовлетворительной.
Нелинейная регрессия
Во многих практических случаях моделирование экономических зависимостей линейными уравнениями дает вполне удовлетворительный результат и может использоваться для анализа и прогнозирования. Однако многие экономические зависимости не являются линейными по своей сути, и поэтому их моделирование линейными уравнениями регрессии не даст положительного результата.
Построение и анализ нелинейных моделей имеют свою специфику. Рассмотрим нелинейные модели, допускающие сведение их к линейным. Такие модели называют линейными относительно параметров моделями. Будем рассматривать модели парной регрессии с целью простоты изложения и графической иллюстрации.
|
из
5.00
|
Обсуждение в статье: Проверка выполнимости предпосылок МНК. Статистика Дарбина-Уотсона |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

