Задания для самостоятельного решения. Определить устойчивость системы, используя алгебраические и частотные критерии

Определить устойчивость системы, используя алгебраические и частотные критерии устойчивости. Определить критический коэффициент усиления.

Структурные схемы системы и параметры для различных вариантов приведены на рис. 8.18 – 8.22.

 

Схема № 8.1.

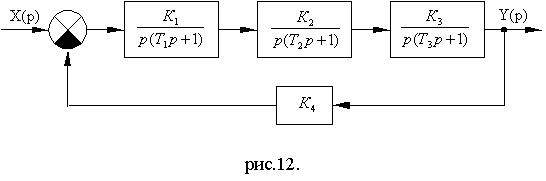
Рис. 8.18

 

 

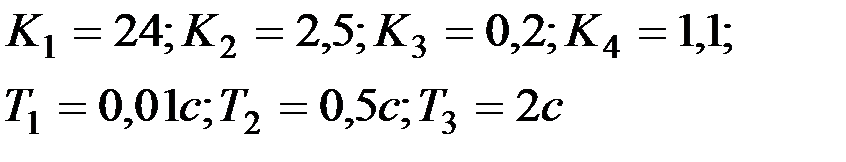
Вариант № 0	Вариант № 1
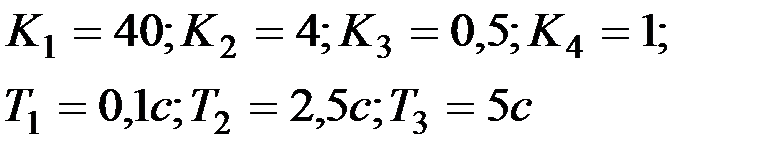
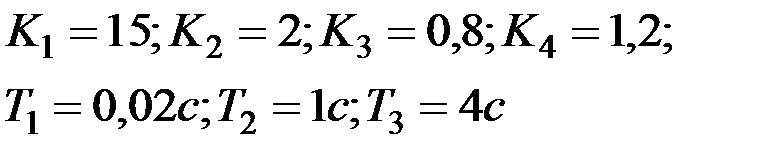
Вариант № 10	Вариант № 11
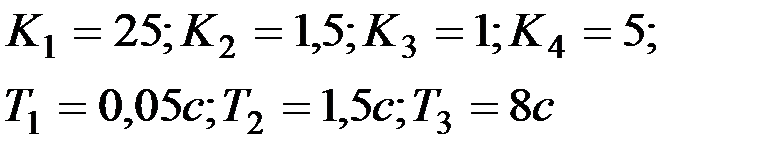
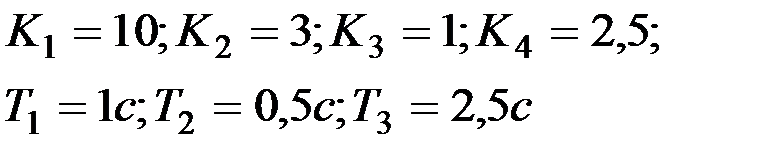
Вариант № 12	Вариант № 13
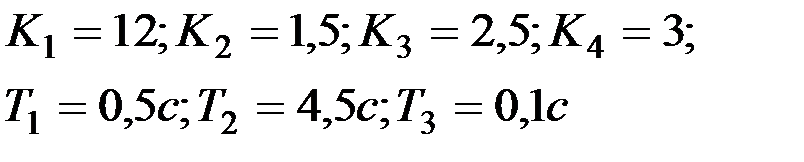
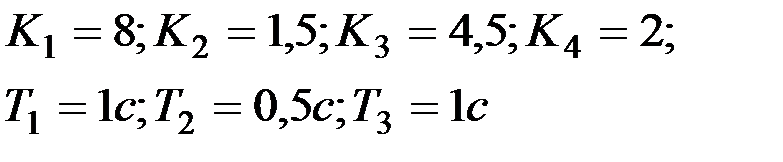
Вариант № 14	Вариант № 15

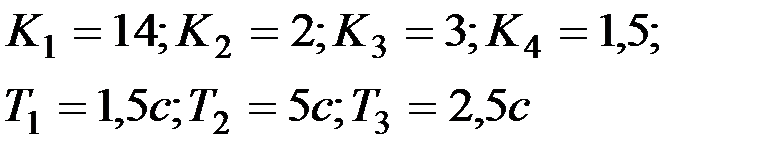
Схема № 8.2.

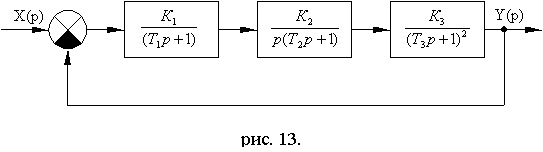
Рис. 8.19

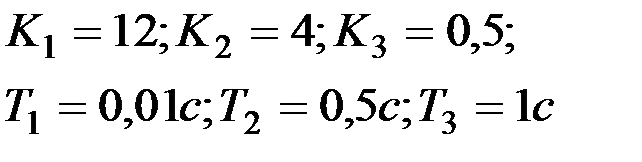
Вариант № 2	Вариант № 3
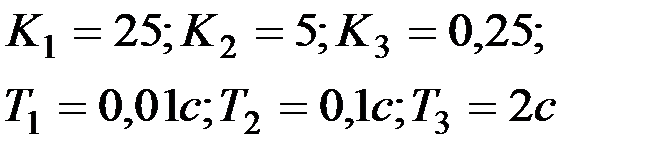
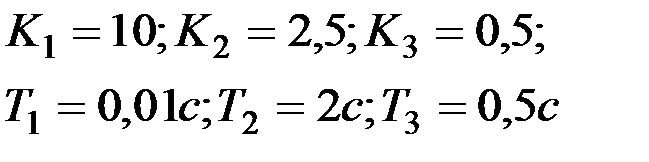
Вариант № 16	Вариант № 17
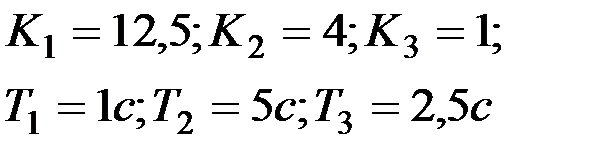
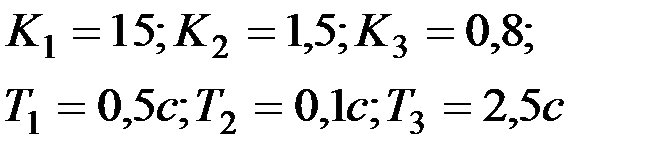
Вариант № 18	Вариант № 19
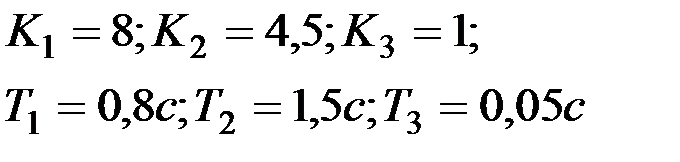
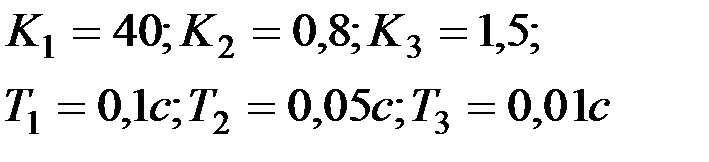
Вариант № 20	Вариант № 21

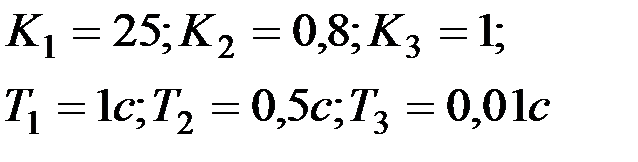
Схема № 8.3

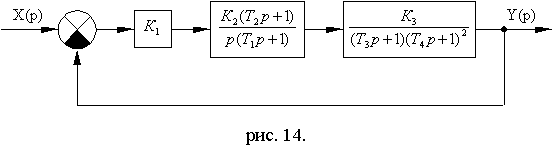
Рис. 8.20

Вариант № 4	Вариант № 5
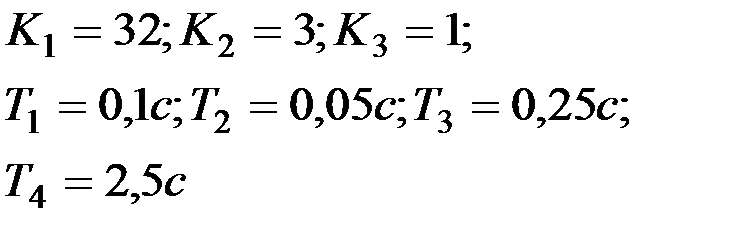
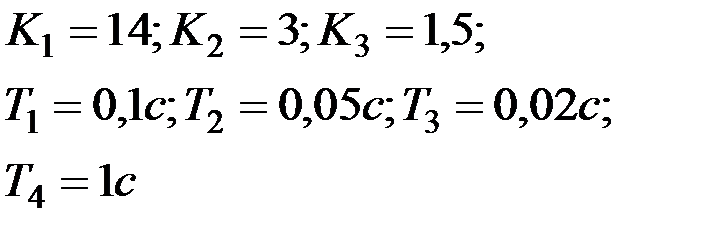
Вариант № 22	Вариант № 23
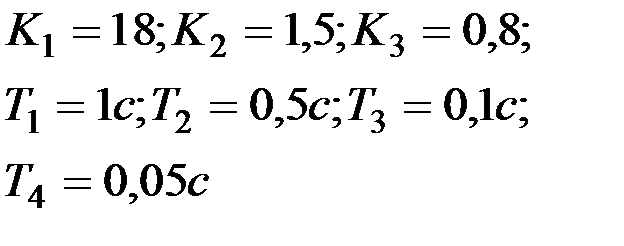
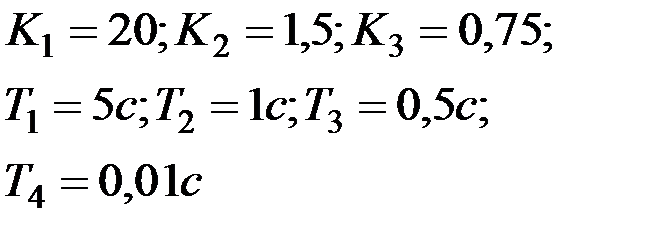
Вариант № 24	Вариант № 25

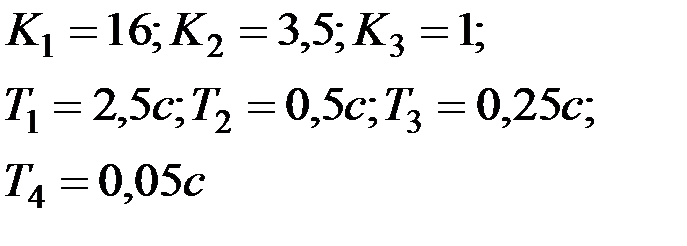
Схема№ 8.4

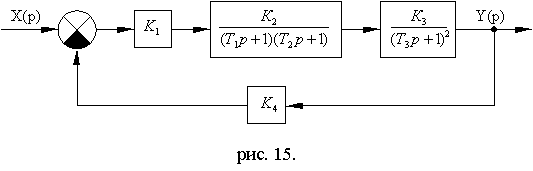
Рис. 8.21

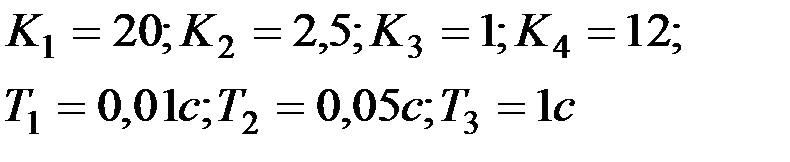
Вариант № 6	Вариант № 7
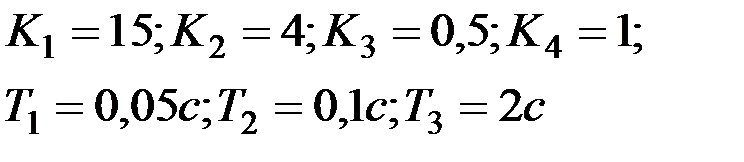
Вариант № 26	Вариант № 27

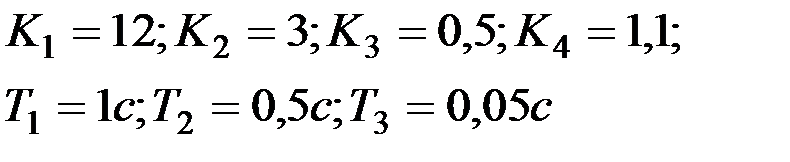
Схема № 8.5

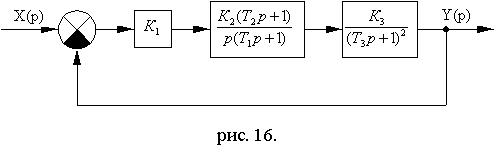
Рис. 8.22

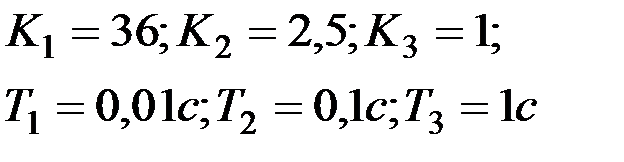
Вариант № 8	Вариант № 9
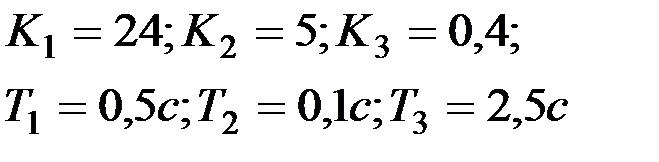
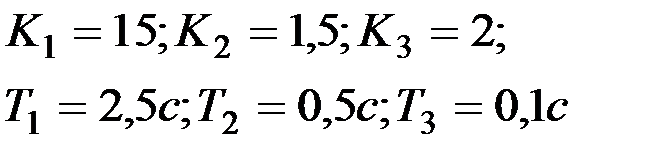
Вариант № 28	Вариант № 29

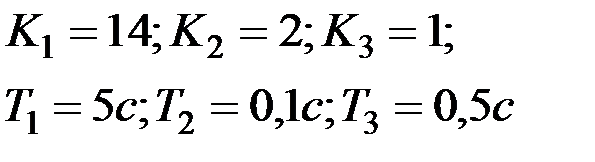
Контрольные вопросы

 

1.Дайте определение устойчивости системы с физической и математической точек зрения.

2.Какой характер имеет переходный процесс в устойчивой и неустойчивой системах?

3.Сформулируйте необходимое условие устойчивости.

4.Что такое критерии устойчивости?

5.Что такое граница устойчивости? Каким образом при этом расположены корни характеристического уравнения системы на плоскости комплексного переменного?

6Сформулируйте принцип аргумента.

7Сформулируйте критерий устойчивости Михайлова.

 

 

Практическая работа № 9

Исследование устойчивости линейных систем на основе построения
графиков вещественной и мнимой функций Михайлова.

 

 

Цель работы: Изучение частотного метода исследования устойчивости линейной системы автоматического управления на основе построения
графиков вещественной и мнимой функций Михайлова

 

Задание: Для оценки устойчивости системы на основе построения
графиков вещественной и мнимой функций Михайлова необходимо выполнить следующие этапы:

- определить передаточную функцию замкнутой системы;

- привести её к дробно-рациональному виду и получить характеристическое уравнение системы;

- в последнем произвести формальную замену оператора р на 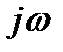и выделить вещественную и мнимую части этого выражения;

- задаваясь произвольно значениями 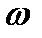от 0 до рассчитать значения и полученные значения свести в таблицу. Рекомендуется посчитать по 2-3 точки для каждого квадранта;

- построить графики вещественной и мнимой функций Михайлова и дать оценку устойчивости системы.

Общие сведения

1. Устойчивость САУ по виду частотных характеристик определяется с помощью частотных критериев, основанных на использовании принципа аргумента Коши, известного из теории функций комплексного переменного. Это критерии Михайлова, Найквиста и D-разбиения.

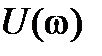Критерий устойчивости Михайлова основан на рассмотрении характеристического многочлена , но имеющего несколько иное представление. Подставим в этот многочлен . В результате получим комплексную функцию . Вещественная часть получена из членов многочлена , содержащих четные степени , а мнимая часть получена из членов с нечетными степенями 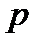. Функция 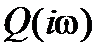отображается в виде годографа на комплексной плоскости (рисунок 9.1). Этот годограф называют годографом Михайлова. Каждому значению соответствуют определенные значения и и определенная точка на комплексной плоскости. При функция 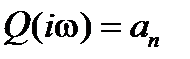, т.е. годограф начинается на действительной оси. При .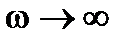

 

 

V(w)

U(w)

w®¥

an

 

Рисунок 9.1 Годограф Михайлова

 

Критерий Михайлова формулируется следующим образом: система устойчива, если годограф , начинаясь на действительной полуоси, огибает против часовой стрелки начало координат, проходя последовательно 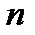квадратов, где 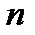-порядок системы (степень характеристического полинома).

На рисунке 9.1 годограф 1 относится к устойчивой САУ, годографы 3, 4. 5, 6, 7 - к неустойчивой САУ. Если годограф проходит через начало координат (кривая 2 на рисунке 9.1), то система находится на границе устойчивости. Действительно, в этом случае существует значение , при котором , т.е. характеристическое уравнение системы, имеет пару сопряженных мнимых корней . А это и означает наличие в системе незатухающих колебаний, т.е. нахождение ее на границе устойчивости. Незначительное изменение параметров системы, в результате которого годограф на рисунке 9.1 отойдет влево от начала координат, делает систему устойчивой, а изменение параметров в другую сторону - неустойчивой.

При построении годографа прежде всего находят точки его пересечения с осями координат. Для этого, определив из уравнения 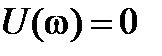значения частот, соответствующих точкам пересечения годографа с мнимой осью, подставляют их в выражение . В результате получают соответствующие ординаты. Аналогично находят точки пересечения с действительной осью, приравнивая к нулю мнимую часть . Как видно из рисунка 9.1, годограф устойчивой системы имеет такой вид, что действительная 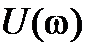и мнимая части функции должны строго по очереди обращаться в нуль, причем должна обращаться в нуль раз, если - четное, раз, если 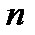- нечетное число, т.е. должна иметь при , соответственно, или корней. Мнимая часть должна обращаться в нуль раз, если 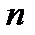- четное, раз, если - нечетное число, т.е. должна иметь при , соответственно, или корней.

При переходе годографа из одного квадранта в другой попеременно обращаются в нуль его вещественная и мнимая части. Отсюда вытекает следствие из критерия Михайлова, заключающееся в том, что для устойчивой системы корни уравнений U (w) = 0 и V (w) = 0 должны чередоваться (условие перемежаемости корней) и общее число этих корней должно быть равно порядку характеристического полинома.

Таким образом, условие перемежаемости корней и можно принять за новый критерий устойчивости (рисунок 9.2).

V

U

w

V

U

w

 

а) б)

 

Рисунок 9.2 Условия перемежаемости корней :

выполняется (а), не выполняется (б)

 

Для устойчивости системы необходимо и достаточно, что бы корни функций и 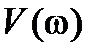строго перемежались. Критерий Михайлова в этой форме иногда называют критерием перемежаемости корней.

U(w)

jV(w)

n=3

устойчива

неустойчива

U(w)

jV(w)

n=3

апериодическая граница

колебательная граница

U(w)

jV(w)

n=5

D(jw)

x

y

На рисунке 9.3, а показана кривая Михайлова неустойчивой сис­темы, у которой нарушена последовательность обхода квадрантов комплексной плоскости. Система находится на апериодической гра­нице устойчивости (рисунок 9.3, б), если кривая при w = 0 начинается в начале координат, и на периодической границе устойчивости, если кривая при w ¹ 0 проходит через начало координат. Заметим, что обо­значения осей U(ω) и V(ω) обычно используются при построении час­тотных характеристик на комплексной плоскости не по всей переда­точной функции, а лишь по ее знаменателю.

 

а б в

 

Рисунок 9.3

 

Число правых корней характеристического уравнения можно определить по формуле , где 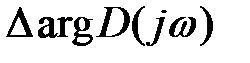– это полное приращение аргумента характеристической функции (суммарный угол поворота). Вектор D(jω) системы пятого порядка (рисунок 14, в) сначала поворачивается на угол 3·(π/2) или три квад­ранта против часовой стрелки, затем возвращается на угол 2·(π/2) или два квадранта по часовой стрелке, что в итоге соответствует полному приращению 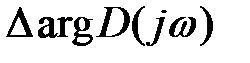= π/2. Отсюда число правых корней m равно 5/2–1/2=2 (числу неправильных пересечений кривой осей координат).

Характеристическая кривая всегда начинается в точке на дейст­вительной оси, удаленной от начала координат на величину a_n. По­этому, если k входит только в свободный член a_n уравнения D(s) = 0, то критические значения k_кр определяются из графика при нулевом значении мнимой координаты V(w) = 0: апериодическая граница по условию a_n = 0, периодическая граница по a_n = |x| + y (рисунок 9.3, а).

Кривая Михайлова представляет собой уходящую в бесконеч­ность развертывающуюся спираль, у которой при высоком порядке уравнения практически не видно начальную часть, вследствие этого ее чертят обычно не в точном масштабе, а лишь фиксируя последова­тельность и места пересечения с осями.

Действительная часть содержит только четные степени переменной ω и называется четной функцией, мнимая часть содержит только нечетные сте­пени переменной ω и называется нечетной функцией.

Пример: оценить устойчивость по критерию Михайлова системы, задан­ной ПФ

 

Выписываем характеристическое уравнение D(s) = s³ + 2s² + 3s + 4 = 0. Производим замену s = jw, снижаем порядок j и группируем

D(jw) = ( jw)³ + 2( jw)² + 3jw + 4 = 4 - 2w² + jw(3 – w²).

 

Здесь 4 - 2w² – это четная (действительная) функция U(w),а w(3 – w²) – это нечетная (мнимая) функция V(w).

Приравнивая поочередно четную и нечетную функции нулю, находим частоты 1,41 и 1,73, соот­ветствующие пересечению кривой с осями коорди­нат, подставляем эти частоты в характеристическую функцию и заполняем таблицу. Строим график – начинаясь на действительной положительной полу­оси при ω = 0, он проходит последовательно против часовой стрелки n = 3 квадрантов комплексной плоскости, уходя в бесконечность при ω = ∞.

 

Таблица частот

w	U(w)	V(w)
¥	-¥	-¥
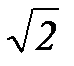=1,41		1,41
=1,73	-2

 

 

Система устойчива (рисунок 9.4, а). Она будет находиться на апериодиче­ской границе устойчивости при a_n = 0 и на периодической границе устойчивости при a_n = 2 + 4 = 6.

U(w)

jV(w)

n=3

-2 4

1.41

U(w)

V(w)

U(w),V(w)

w

1.41

-2

n=3

1.41

1.73

а б

 

Рисунок 9.4

 

Существует еще одна формулировка критерия Михайлова, ос­нованная на анализе графиков четной и нечетной функций. Она носит название следствия или второй формы критерия Михайлова.

Система устойчива, если четная U(w) и нечетная V(w) функции при изменении частоты w от нуля до плюс бесконечности обраща­ются в нуль поочередно, начиная с нечетной функции, т.е. их корни перемежаются. Это вытекает из условия последовательного прохож­дения квадрантов. Для построения графика (рисунок 9.4 б) использу­ется та же таблица частот, что и в первой форме.

Очевидно, что при нарушении очередности пересечения функ­циями оси абсцисс (частот) система неустойчива (рисунок 9.5, а). Сис­тема находится на апериодической границе устойчивости (рисунок 9.5, б), если обе функции начинаются в начале координат, и на периодиче­ской границе устойчивости (рисунок 9.5, в), если при w ¹ 0 кривые пе­ресекают ось частот в одной точке. В остальном диапазоне изменения функций условия устойчивости при этом не должны нарушаться. Час­тота w, при которой система находится на периодической границе ус­тойчивости, равна частоте незатухающих колебаний.

 

 

а б в г

 

Рисунок 9.5

 

На графике с кривой Михайлова обязательно должен указывать­ся порядок системы n, так как при его отсутствии может быть сделан ошибочный вывод. В данной работе необходимо:

Оценить устойчивости линейной системы автоматического управления на основе построения графиков вещественной и мнимой функций Михайлова и выполнить расчеты задания № 1

Задание №1

1. Определить устойчивость автоматической системы на основе построения графиков вещественной и мнимой функций Михайлова, если характеристическое уравнение имеет вид

 

вариант	а0	а1	а2	а3
	0,004	0,5
	0,005	0,4
	0,012	0,20
	0,058	0,8
	0,890	0,40
	0,47	0,7
	0,65	0,1

 

2. Исследовать влияние коэффициента α на устойчивость автоматической системы на основе построения графиков вещественной и мнимой функций Михайлова, если характеристическое уравнение имеет вид

 

 

где а0=0,000524 , а1 =0,0589, а2 = 1,014 , а3 = 2,619+35*α , а4=87 ,если коэффициент α принимает значения 0,02; 0,115 ; 0,25 ; 0,4.

 

3. На основе построения графиков вещественной и мнимой функций Михайлова определить граничное значение коэффициента передачи регулятора К_р, если характеристическое уравнение системы имеет вид

 

 

где а0=0,004 , а1 =0,35, а2 = 4,2 , а3 = 30 , Ко=2

 

4. Определить на основе построения графиков вещественной и мнимой функций Михайлова устойчивость автоматической системы, используя условие перемежаемости корней, уравнение свободного движения которой имеет вид

 

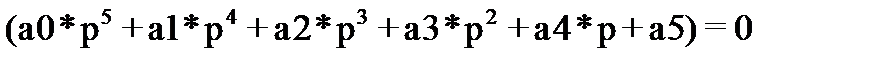
где а0=6*10^-4 , а1 =10^-2, а2 = 0,2 , а3 = 1, а4 = 1,8, а5 = 2

а0=7*10^-4 , а1 =10^-2, а2 = 0,8, а3 = 47, а4 = 0,41, а5 = 0

а0=1*10^-4 , а1 =10^-1, а2 = 0,3 , а3 = 5, а4 = 1,22, а5 = 5

а0=3*10^-4 , а1 =10^-2, а2 = 0,12 , а3 = 0,8, а4 = 4, а5 = 100

 

5. Определить устойчивость автоматической системы на основе построения графиков вещественной и мнимой функций Михайлова, для системы со следующей структурной схемой

 

 

Вариант	к1	к2	к3	к4	Т1	Т2	Т3	Т4
		0,58			0,1	0,5		4,7
		0,34		1,5	0,1	0,6		1,5
		0,69		7,6	0,1	0,7		6,4
		0,33		8,6	0,1		0,5	3,8
		0,10		4,5	0,1	1,0

 

6. Определить устойчивость замкнутой и разомкнутой системы автоматического управления на основе построения графиков вещественной и мнимой функций Михайлова со следующей структурной схемой

 

 

К1= 120 Т1= 0,25 ξ=0,05

 

7. Определить устойчивость замкнутой и разомкнутой системы автоматического управления на основе построения графиков вещественной и мнимой функций Михайлова со следующей структурной схемой

 

 

 

К1= 48 Т1= 0,47 ξ=0,5 К2=10

 

8. Определить устойчивость замкнутой и разомкнутой системы автоматического управления на основе построения графиков вещественной и мнимой функций Михайлова со следующей структурной схемой

 

 

 

Вариант	к1	к2	Т1	Т2	ξ
			0,1	2,56	0,5
			0,23	5,63	0,6
			0,14	4,5	0,7
			0,19	4,7
			0,42	1,28	1,0