 |
Главная |
Пример преобразования регулярной грамматики к автоматному виду
|
из
5.00
|
Рассмотрим в качестве примера следующую простейшую регулярную грамматикy: G({"a","(","*",")","{","}"},{S,C,K},P,S) (символы а, {, *, ), {, }из множествa терминальных символов грамматики взяты в кавычки, чтобы выделить их среди фигурных скобок, обозначающих само множество):
P:
S → C*) | K}
С → (* | Ca | C{ | C} | C( | С* | С)
К → { | Ka [ К( | К* | K) | K{
Преобразуем ее в автоматный вид.
Шаг 1.Построим множество VN' - {S. С, K}.
Шаг 2.Начинаем просматривать множество правил P грамматики G.
Для правила S → C*) во множество VN' включаем символ S1, а само правило разбиваем на два: S→ S1) и S1→C*; включаем эти правила во множество правил P'.
Правило S → K} переносим во множество правил P' без изменений.
Для правила С → (*во множество VN' включаем символ C1, а само правило разбиваем на два: С→ С1* и С1→(; включаем эти два правила во множество правил Р'.
Правила С → Ca | C{ | C} | C( | С* | С) переносим во множество правил Р' без изменений.
Правила К → { | Ka [ К( | К* | K) | K{ переносим во множество правил Р' без изменений.
Шаг 3.Правил вида A → B или вида A → λ во множестве правил P' не содержится.
Шаг 4.Переходим к шагу 5.
Шаг 5.Целевым символом грамматики G' становится символ S.
В итоге получаем автоматную грамматику:
G' ( {"a", "(", "*", ")", "{","}"}, {S,S1,C,C1,K},P',S):
P':
S → S1) | K}
S1 → С*
С → C1* | Ca | C{ | C} | C( | С* | С)
C1 → (
К → { | Ka | K( | К* | К) | K{
Алгоритм построения конечного автомата на основе автоматной леволинейной грамматики
Построение KA M(Q,V, δ,q0,F) на основе автоматной леволинейной грамматики G(VT,VN,P,S) выполняется по следующему алгоритму:
Шаг 1.Строим множество состояний автомата Q. Состояния автомата строятся таким образом, чтобы каждому нетерминальному символу из множества VN грамматики G соответствовало одно состояние из множества Q автомата M. Кроме того, во множество состояний автомата добавляется еще одно дополнительное состояние, которое будем обозначать H. Сохраняя обозначения нетерминальных символов грамматики G, для множества состояний автомата M можно записать: Q = VN 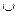 {H}.
{H}.
Шаг 2.Входным алфавитом автомата M является множество терминальных символов грамматики G: V = VT.
Шаг 3.Просматриваем все множество правил исходной грамматики.
Если встречается правило вида A → t 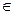 P, где A
P, где A 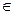 VN, t
VN, t 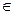 VT, то в функцию переходов δ (H,t) автомата M добавляем состояние A: A
VT, то в функцию переходов δ (H,t) автомата M добавляем состояние A: A 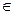 δ (H,t).
δ (H,t).
Если встречается правило вида A → Bt 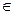 P, где A,B
P, где A,B 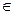 VN, t
VN, t 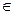 VT, то в функцию переходов δ (Н,t) автомата M добавляем состояние A: A
VT, то в функцию переходов δ (Н,t) автомата M добавляем состояние A: A 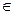 δ (B,t).
δ (B,t).
Шаг 4.Начальным состоянием автомата M является состояние H: q0 = H.
Шаг 5.Множество конечных состояний автомата M состоит из одного состояния. Этим состоянием является состояние, соответствующее целевому символу грамматики G: F = {S}.
На этом построение автомата заканчивается.
|
из
5.00
|
Обсуждение в статье: Пример преобразования регулярной грамматики к автоматному виду |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

