Алгебраические неравенства с одной переменной

 

Неравенством с одной переменной х называют соотношения вида:

1)

2) (21)

3)

4)

где – некоторые выражения зависящие от переменной х при условии, что ставится задача нахождения всех тех значений , при которых эти неравенства верны. Неравенства 1) и 2) называются строгими, а 3) и 4) – нестрогими.

Решением неравенств типа (21) называют такое значение переменной х, при котором оно обращается в верное числовое неравенство.

Решить неравенство – значит найти множество всех его решений или доказать, что неравенство решений не имеет.

Два неравенства называются равносильными, если они имеют, одно и то же множество решений.

 

Свойства равносильности неравенств:

 

1) неравенства и – равносильны;

2) неравенства и – равносильны;

3) если то и – равносильны;

4) если то – равносильны;

5) неравенства и – равносильны;

6) неравенства и равносильны;

7) если , (22)

и , то неравенство (22) равносильно неравенству . (23)

Аналогичные свойства имеют место для всех остальных неравенств.

Неравенство вида:

где – называется линейным неровенством.

Неравенство вида

называется квадратнымнеравенством.

В основе решения квадратного неравенства лежит графический метод. В зависимости от знака коэффициента а и дискриминанта D возможен один из шести случаев расположения графика функций (табл. 1).

Табл. 1

D а	– корни	– корень	нет корней

 

Решение квадратного неравенства находят по расположению соответствующего графика функции относительно оси

Неравенство

(24)

где – многочлен степени , называется неравенством высшей степени.

Основной метод решения неравенств типа (24) – метод интервалов. Он состоит в следующем.

1. Многочлен необходимо разложить на множители. Допустим, получено неравенство

где квадратный трехчлен имеет

2. Коэффициент А и квадратный трехчлен следует «отбросить». Если или то знак неравенства при этом изменяется на противоположный.

Допустим, что приходим к неравенству вида:

(25)

где корни расположены в порядке возрастания.

3. Корни наносят на числовую ось. Справа от самого большого корня ставят знак «+» над промежутком, далее идет чередование знаков.

4. Необходимо нарисовать кривую знаков.

5. Штрихуют те промежутки, которые отвечают смыслу неравенства (т.е. для неравенства (25) это множество тех значений х, для которых кривая знаков находится под осью Ох).

6. записывают ответ в виде промежутка, объединения промежутков (если их несколько) или множества из отдельных точек.

Если в результате преобразований неравенство приняло вид

где и расположены в порядке возрастания, то для решения используют обобщенный метод интервалов. Он состоит в следующем.

1. Корни наносят на числовую ось.

2. Справа от самого большого корня ставят на промежутком знак «+».

а) если – нечетное число, то при «переходе» через корень знак изменится на противоположный (т.е. следующий промежуток отметим знаком «–»);

б) если – четное число, то при переходе через корень знак не изменится;

в) аналогично при «переходе» через остальные корни.

3. Необходимо нарисовать кривую знаков.

4. Штрихуют те промежутки, которые соответствуют смыслу неравенства.

5. Ответ записывают в виде промежутка, объединения промежутков (если их несколько) или множества из отдельных точек.

Метод интервалов – частный случай обобщенного метода интервалов.

Неравенства типа

(26)

где – некоторые многочлены, называется дробно-рациональным неравенством. Его запись (26) называется стандартным видом дробно-рационального неравенства.

Основными методами решения данных неравенств являются:

– метод интервалов (или обобщенный метод интервалов);

– метод замены переменной.

При решении строгих неравенств типа (26) вначале их записывают в виде

,

а затем используют метод интервалов или обобщенный метод интервалов.

Решение нестрогих неравенств

сводится к решению системы

В любом случае, при изображении нулей знаменателя на числовой оси точки, представляющие их, выкалываются.

Неравенства вида

называются двойными неравенствами, они равносильны системе:

Решением системы неравенств называют такие значения переменной, при которых каждое из заданных неравенств обращается в верное числовое неравенство.

При решении совокупности неравенств, полученные решения каждого неравенства объединяются.

Замечание: решать неравенство вида

по основному свойству пропорции нельзя, т.к. в общем случае выражения являются знакопеременными. Вначале их следует привести к стандартному виду (26).

 

Пример1. Решить неравенство

.

Решение.

Данное неравенство равносильно неравенству:

.

Преобразуем его разложив на множители:

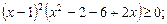
Используем обобщенный метод интервалов (рис. 3).

 

Рис.3

Заметим, что – двукратный корень, при переходе через данное значение, знак не меняется. Поскольку неравенство нестрогое, в качестве решения подходят также те значения, при которых многочлен обращается в 0, т.е. .

Получаем ответ: .

Пример 2.Решить неравенство

Решение. ОДЗ: .

С учетом ОДЗ данное неравенство равносильно неравенству:

;

;

;

.

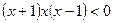Методом интервалов решаем последнее неравенство (рис. 4), учитывая ОДЗ.

Рис.4

Получаем решение:

Пример 3.Найти наибольшее решение системы неравенств

Решение.

Заданная система равносильна системе:

 

Рис. 5

Решением (рис. 5) является промежуток: . Наибольшее значение на данном промежутке

 

Пример 4.Решить совокупность неравенств

Решение.

Решим каждое неравенство заданной совокупности отдельно:

.

Приходим к неравенству

.

Используя метод интервалов (рис. 6), получаем

 

 

Рис. 6

.

2) Решаем второе неравенство совокупности. Находим корни и разлагаем на множители, получаем (рис. 7)

.

 

 

Рис.7

В итоге имеем: .

Объединяя полученные решения двух неравенств совокупности (рис 8), приходим к ответу: .

 

 

Рис. 8