 |
Главная |
Построение статической модели динамики объекта управления
|
из
5.00
|
Поведение объекта управления в динамике можно описать непрерывным дифференциальным уравнением
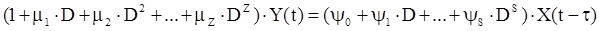 ,
,
где  - выходной и входной сигналы объекта; D – дифференциальный оператор, равный
- выходной и входной сигналы объекта; D – дифференциальный оператор, равный  ;
; 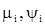 - неизвестные параметры; t - время запаздывания.
- неизвестные параметры; t - время запаздывания.
Для дискретных сигналов связь между входным Х(t) и выходным Y(t) сигналами в момент времени t=0, 1, 2… описывается разностным уравнением
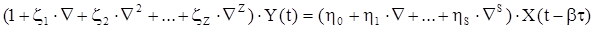 . (25)
. (25)
Линейную модель (25) можно эквивалентным образом описать с помощью оператора сдвига назад 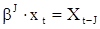 путем замены
путем замены 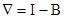 , в ходе преобразований получим:
, в ходе преобразований получим:
 . (26)
. (26)
Другими словами выход Yt и вход Xt связаны линейным фильтром:
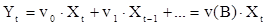 ,
,
где v0, v1 – дискретная функция отклика на единичный импульс.
Теперь рассмотрим решение задачи идентификации или нахождение коэффициентов dI и wj модели (26). Пусть известны вход Xt и выход Yt объекта.
Полагаем, что входной процесс Xt описывается моделью авторегрессии третьего порядка:
 . (27)
. (27)
Опишем последовательность нахождения Фi , i=1, 2, 3 в уравнении авторегрессии третьего порядка (27), представленной в виде
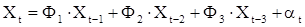 . (28)
. (28)
Умножим (28) на Xt-k и перейдя к математическим ожиданиям величин, получим разностное уравнение
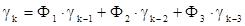 . (29)
. (29)
Отметим, что  , а поскольку импульсы
, а поскольку импульсы 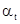 не коррелируются с
не коррелируются с 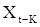 . Параметр
. Параметр  называется автоковариацией с задержкой К и вычисляется по формуле:
называется автоковариацией с задержкой К и вычисляется по формуле:
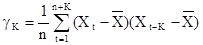 , К=0, -1, -2… (30)
, К=0, -1, -2… (30)
Введем коэффициент корреляции
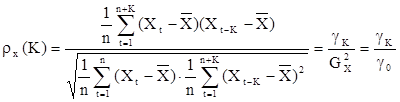 . (31)
. (31)
Разделив левую и правую часть уравнения (30) на 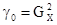 , получим:
, получим:
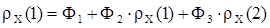 ;
;
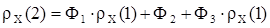 ;
;
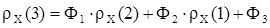 . (32)
. (32)
Зная 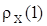 ,
,  ,
, 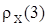 , систему уравнений (32) легко разрешить относительно Фi, i=1, 2, 3.
, систему уравнений (32) легко разрешить относительно Фi, i=1, 2, 3.
Теперь перейдем к определению дискретной весовой функции: v0, v1, ...vK , для этого определим коэффициент взаимной ковариации
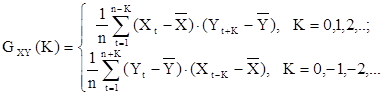 (33)
(33)
Коэффициент взаимной корреляции:
 .
.
С помощью рядов (28) вычислим Ga, Gb, at и Bt, t=0, 1, 2,…n. Затем, умножая обе части уравнения (28) на Bt+k, Gb и разделив на Ga и Gb получим коэффициент взаимной корреляции
 , причем
, причем 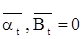 .
.
Оценки весовой функции вычисляются по формуле
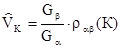 , К=0, 1, 2,…10.
, К=0, 1, 2,…10.
Если окажется, что оценки  малы по сравнению с
малы по сравнению с 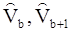 , то это значит запаздывание равно B. Для модели (26) оценки dI и
, то это значит запаздывание равно B. Для модели (26) оценки dI и 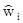 определяются следующим образом:
определяются следующим образом:
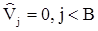 ,
,
 ,
,

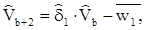
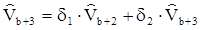 .
.
Из последних двух уравнений вычисляются оценки  и
и  , которые при подставке в третье и четвертое уравнения позволяют определить оценки
, которые при подставке в третье и четвертое уравнения позволяют определить оценки 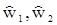 .
.
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ
1 Закгейм А.Ю. Введение в моделирование химико-технологических процессов. Математическое описание процессов. – М.: Химия, 1973. – 224 с.
2 Советов Б.Я., Яковлев С.А. Моделирование систем: Учебник для вузов по спец. «Автоматизированные системы управления». – М.: Высш. шк., 2001. – 271 с.: ил.
3 Харин Ю.С., Малюгин В.И., Кирлица В.П. и др. Основы имитационного и статистического моделирования.: Учеб. пособие – Мн.: Дизайн ПРО, 1997,- 288 с.:ил.
4 Кузичкин Н.В. и др. Методы и средства автоматизированного расчета химико-технологических систем.: Учеб. пособие для вузов – Л.: Химия, 1987. – 152 с.
КРАТКИЙ КУРС ЛЕКЦИЙ ПО ДИСЦИПЛИНЕ «МОДЕЛИРОВАНИЕ ОБЪЕКТОВ И СИСТЕМ УПРАВЛЕНИЯ ОТРАСЛЬЮ»
для студентов дневной и заочной форм обучения специальности 53 01 01 - «Автоматизация технологических
процессов и производств»
Составитель к.т.н., Иванова Ирина Дмитриевна
Редактор Бажанова Т.Л.
Технический редактор Щербакова А.А
___________
Подписано в печать_____________ Формат 60х84 1/16
Печать офсетная. Усл. печ. л.___________ Уч.-изд. л.______
Тираж ______экз.______Заказ_________ Бесплатно
Лицензия № 226 от 12.02.2003 г.
___________
Отпечатано на ризографе МГУП
212027, г. Могилев, пр-кт Шмидта, 3.
|
из
5.00
|
Обсуждение в статье: Построение статической модели динамики объекта управления |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

