 |
Главная |
Моделирование некоторой химической реакции
|
из
5.00
|
Предположим, что компоненты А и В вступают в некоторой емкости в химическую реакцию, протекающую в соответствии со следующим стехиометрическим уравнением:
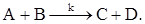
Модель реактора идеального смешивания представлена на рисунке 5. В самой емкости и в выходном потоке содержатся 4 компоненты: А, В, С, D. Выражение, определяющее скорость реакции выглядит так
R=kVCACB,
где R – скорость реакции в объеме V, моль/ед. времени;
CA и CB - концентрации компонент соответственно А и В;
k – константа скорости реакции.
 |
Рисунок 5 – Модель реактора идеального смешивания (емкость с мешалкой)
Рассмотрим R как входной параметр для балансов по компонентам А и В и как выходной – для С и D. Уравнение материального баланса выглядит следующим образом:
[скорость накопления] = [приток] - [сток]. (5)

Из уравнения (5) определяется объем системы как
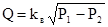 ,
,
где (Р1-Р2) – перепад давления;
kв – коэффициент пропускной способности.
Для каждой из четырех компонент запишем уравнения материальных балансов:
 - материальный баланс компонента А,
- материальный баланс компонента А,
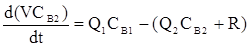 - компонента B,
- компонента B,
 - компонента С,
- компонента С,
 - компонента D,
- компонента D,
где  - скорость накопления.
- скорость накопления.
Из уравнений материальных балансов по отдельным компонентам, вводя в них потоки QjCi, определяем количество компонентов VCi. Поскольку объем V в эти уравнения вводится извне, то можно определить интересующую нас концентрацию Ci на выходе из емкости.
По схеме:
Вход ® Модель системы ® Выход
строим совмещенную математическую и концептуальную модель.
Моделирование гидравлической емкости
Рассмотрим емкость, в которую поступает жидкость с известным расходом Q1 и расходом Q2 – вытекающей жидкости. Требуется найти величину уровня жидкости в емкости для любого момента времени t, если Q1 и Q2 изменяются известным образом во времени (см. рисунок 5).
Согласно определения (5), записывается уравнение материального баланса, где скорость накопления жидкости – это изменение объема жидкости во времени т.е. dV/dt.
Если площадь поперечного сечения емкости равна S (где S – const), а уровня жидкости H, то объем жидкости равен SH, тогда
 . (5а)
. (5а)
По полученной математической модели строим концептуальную модель, совмещенную с математической по схеме:
Вход ® Модель системы ® Выход.
Модель отражает тот факт, что задавая величины расходов Q1 и Q2, как непрерывные функции времени, можно вычислить величину производной dH/dt также как непрерывную функцию времени. Если интегрировать эту производную, то получаем величину Y – уровень жидкости в емкости. Для решения уравнений необходимо задать Q1(t), Q2(t) и начальное значение уровня H0.
|
из
5.00
|
Обсуждение в статье: Моделирование некоторой химической реакции |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

