Проводники в электрическом поле

При внесении проводника в электрическое поле носители заряда в нем приходят в движение под действием сил электрического поля. В результате у концов проводника возникают заряды противоположного знака, их назы­ва­ют индуцированными зарядами (см. раздел 1.1.). Поле этих зарядов направлено противоположно внешнему полю. Перераспределение зарядов продол­жа­ется до тех пор, пока напряженность внутри проводника не станет равной нулю. Таким образом, всюду внутри проводника

Е= 0 (28) В соответствии с (19) это означает, что потенциал внутри проводника должен быть постоянен ( ) и равен потенциалу на его поверхности. В свою очередь, постоянство потенциала на поверхности проводника означает, что его поверхность является эквипотенциальной и силовые линии электри­чес­ко­го поля перпендикулярны к этой поверхности в каждой ее точке. Если внутри проводника имеется полость, то при равновесном распределении индуцированных зарядов поле внутри нее также обращается в нуль. На этом основана электростатическая защита. Если какой-то объект хотят защитить от воздействия внешних электростатических полей, его окружают проводящим экраном. Внутри экрана внешнее поле компенсируется полем индуцированных зарядов, возникающих на его поверхности. Если проводящему телу сообщить некоторый заряд q, то он распределится так, чтобы соблюдались условия равновесия. Рассмотрим замкнутую поверхность внутри проводника. Поле внутри проводника отсутствует, поток вектора Е через эту поверхность равен нулю и согласно теореме Гаусса алгебраическая сумма зарядов внутри по­­верхности тоже будет равна нулю. Таким образом, в любом месте внутри объема проводника отсутствуют избыточные заряды. Все они расположатся по поверхности проводника с некоторой плотностью s.

Рассмотрим поверхность цилиндра, образующая которого нормальна к поверхности проводника, а основания, площадь которых dS расположены одно снаружи проводника, а одно внутри (рис. 10).

Рис. 10

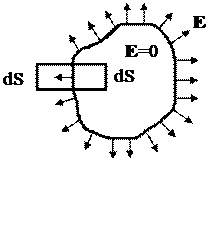Поток вектора Е через эту поверхность пред­ставляет собой поток через боковую поверхность (он равен нулю, т.к. нормаль к боковой по­верхности перпендикулярна к Е), поток через внутреннее основание (он равен нулю, т.к. внутри проводника поле отсутствует) и потока через внеш­нее основание (этот поток отличается от нуля). Т.к. вблизи провод­ника Е перпендикулярен поверхности, то поток через внешнее основа-

ние (он равен потоку через всю поверхность цилиндра) равен EdS и теорему Гаусса для этой поверхности можно записать

, откуда

(29) Формула (29) показывает, что напряженность поля вблизи проводящей по­верх­ности вне проводника определяется поверхностной плотностью заряда на нем. Заряды же эти распределяются по поверхности неравномерно. Наи­боль­шая их плотность имеет место вблизи заострений. У таких мест по (29) велика и Е. Это приводит к интересному явлению «стекания» заряда с метал­ли­ческих острий. В больших полях воздух вблизи острий ионизируется. Ионы с тем же знаком заряда, что и у острия, движутся от острия, ионы с противоположным знаком движутся к острию и уменьшают его заряд. Дви­жущиеся от острия ионы увлекают нейтральные молекулы воздуха, отчего возникает электрический ветер. Его можно обнаружить по отклонению пламени свечи, поднесенной к острию.

 

 

Электрическая емкость

Рассмотрим некоторое уединенное проводящее тело. Если сообщить ему заряд q₁, то тело относительно бесконечно удаленной точки приобретет потенциал j₁. При сообщении этому телу другого заряда q₂ потенциал будет j₂, для заряда q₃ это будет j₃ и т.д. Интересно отметить, что при этом отношение заряда, сооб­щен­ного телу, к величине возникающего при этом на теле потенциала будет величиной посто­ян­ной и не будет зависеть от величины заряда, переданного телу. Для другого те­ла это отношение будет тоже величиной постоянной, но сама величина отношения будет уже иной. Таким образом, появляется возможность ввести еще одну харак­те­ристику проводящего тела. Эту характеристику назвали электрическая емкость. Если обозначить электроемкость как С, то по сказанному выше

, (30) где q – сообщенный телу заряд, а j – возникающий при этом потенциал этого те­ла. В системе СИ за единицу электроемкости (часто говорят емкости тела) прини­мают емкость, которой обладает уединенное проводящее тело, которое при сооб­ще­нии ему заряда в 1 Кл, приобретает потенциал в 1 В. Такую единицу электроем­кости называют фарад (Ф). Фарад очень большая емкость (скоро мы в этом убе­дим­ся), поэтому на практике в электро- и радиотехнике часто пользуются более мелкими единицами электроемкости пикофарад (пкФ) и микрофарад (мкФ).

1 Ф = 10⁶мкФ = 10¹²пкФ.

Подсчитаем электрическую емкость уединенной проводящей сферы. Ее потенциал относительно бесконечно удаленной точки равен

, R – радиус сферической поверхности. Подставив j в (30), получаем

. (31) Таким образом, емкость уединенного тела прямо пропорциональна его размерам (в нашем случае радиусу). Для оценки величины единицы емкости попробуем оценить емкость Земного шара. Его радиус . Подставим этот радиус в (31)

С = 4×3,14×8,85×10^-12Ф/м×6,4×10⁶ м = 7,11×10^-4Ф = 711 мкФ. Таким образом, фарад действительно большая единица, если такой емкостью обладает шар, радиус которого в 1/0,000711 = 1406 раз больше радиуса Земли.

Как мы только что увидели, уединенные проводники обладают малой емкостью. Однако емкость уединенного тела можно значительно увеличить, если поднести к нему другое тело или тела. Поскольку на практике нужны устройства с большой электроемкостью, это обстоятельство стали использовать для создания таких устройств. В основе описанного возрастания емкости тел при приближении к ним других тел лежит следующее. При сближении тел заряды, противоположные по знаку заряду рассматриваемого проводника, располагаются ближе к проводнику, чем одноименные, и оказывают большое влияние на его потенциал. Потенциал проводника уменьшается, а емкость, как видно из (30), растет.

Систему двух (или более) проводящих тел, емкость которых уже не зависит от других окружающих тел, принято называть конденсатором. Сами эти тела на­зы­вают обкладками конденсатора. Силовые линии, исходящие из одной обкладки заканчиваются на другой (других). В зависимости от геометрии обкладок различа­ют 3 вида конденсаторов. С плоским конденсатором мы уже сталкивались. Обклад­ки плоского конденсатора представляют собой две параллельные пласти­ны, расстояние между которыми мало по сравнению с их размерами. Простым конден­сатором является также сферический конденсатор, обкладки которого две кон­цент­рические сферы. Трубчатый или цилиндрический конденсатор имеет обкладки в форме коаксиальных цилиндров. Для любой формы конденсаторов можно легко экспериментально установить, что с ростом площади обкладок и с уменьшением расстояния между ними емкость конденсатора возрастает.

Попробуем теперь вычислить емкость самого простого плоского кон­денсатора. Разность потенциалов между его обкладками дается формулой (24), а заряд на обкладках площадью S находится легко . Подставив значения заряда и разности потенциалов в (30), получаем 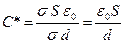(32)

В формуле (32) d – расстояние между обкладками. Емкость конденсатора легко увеличить, не меняя его геометрию, а заполнив пространство между обкладками диэлектриком. От этого емкость конденсатора возрастает в e раз. Величину e назы­вают относительной диэлектрической проницаемостью диэлектрика. К этому понятию мы вернемся, рассматривая электрические поля, создаваемые зарядами внутри диэлектрика. Итак, для плоского конденсатора, заполненного диэлектри­ком, получаем

(33) Анализируя выражение (33) нетрудно увидеть, что, как и следует из экспери­мента, емкость можно увеличить, увеличивая S и уменьшая d.

Хотя промышленность выпускает множество самых разных конденсаторов, отличающихся формой обкладок, видом диэлектрика, емкостью, но часто на прак­тике приходится сталкиваться с необходимостью использовать конденсатор с но­ми­налом, которого нет в наличии. В этих случаях можно с целью подбора нуж­ной емкости составить батарею из конденсаторов, имеющихся в наличии. Проще всего рассчитывать емкости таких батарей, если конденсаторы в них включены последо­вательно или параллельно. Посмотрим, как это можно сделать. Начнем с последова­тель­ного включения. Оно изображено на рис. 11.

		C1 C2

 

 

Два конденсатора С₁ и С₂, состав­ляющие эту батарею, включены последовательно. Наша задача найти емкость С, которой можно заменить эту батарею конденсаторов. Создав разность потенциа­лов между обкладками конденсаторов, входящих в батарею, мы заряжаем их. До­пустим, заряд левой обкладки конденсатора С₁ является отрицательным (его мо­дуль обозначим q₁), а заряд правой обкладки конденсатора С₂ является положит­ельным (обозначим q₂). На внутренних обкладках конденсатора при этом происхо­дит смещение зарядов. Внутренняя обкладка конденсатора С₁ приобретает заряд q₁, а конденсатора С₂ – заряд q₂. До зарядки конденсаторов суммарный заряд на внутренних обкладках был равен нулю и т.к. через идеальный конденсатор заряд пройти не может, он таким и остается. Поэтому +q₁- q₂=0 и q₁= q₂, т.е. заряды на последовательно включенных конденсаторах одинаковы. Можно утвер­ждать, что заряд, подошедший при зарядке к конденсатору С q= q₁= q₂, т.к. этот конденсатор заменяет последовательно включенные конденсаторы. Итак, для трех рассматри­ва­емых нами конденсаторов можно написать Найдя из этих равенств , , 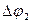и подставив в

(34) получаем

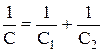, (35) откуда

. (36) При последовательном включении нескольких конденсаторов равенство (35) переходит в

(37)

Теперь остановимся на параллельном включении конденсаторов. Такая батарея приведена на рис. 12.

C1

 

В этом случае заряд, подходящий к обкладкам конденсатора С равен сумме зарядов, подходящих к обкладкам конденсато­ров С₁ и С₂

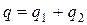(38) Разности же потенциалов между обкладками всех конденсаторов одинаковы и равны U. Найдя из заряды и подставив их в (38) получаем

(39) При параллельном включении большого числа конденсаторов получаем

(40)