Метод наименьших квадратов

 

Если задача может быть описана моделью, определенной линейной системой уравнений, аналогичных уравнению времени пробега, для вывода решения можно использовать разложение по методу наименьших квадратов. Приведем краткое описание этого метода применительно к разложению наблюденных времен пробега на составляющие статики точек взрыва и приема.

Рис.3.101 Сумма ОСТ наземной съемки с примененной полевой статикой.

 

Рассмотрит геометрию луча на рис.3.98а, проходящего от j-того ПВ (А) к i-тому сейсмоприемнику (D). Время пробега t_ij для вступления преломленной волны можно выразить в виде линейной комбинации трех элементов (Farrell и Euwema, 1984):

tij = sj + ri + xij/vb

(3.45)

где x_ij = AD и

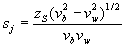
(3.46а)

и

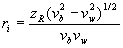
(3.46b)

для общего случая различных глубин до коренных пород под точками (z_S) и приема (z_R). Неизвестными величинами являются s_j – часть отрезка, отсекаемого продолжением годографа ПВ на оси времен, ассоциированная с положением j-того источника, и r_j – часть отрезка, ассоциированная с положением i-того сейсмоприемника. Поскольку вступления преломленной волны обычно исправляются за линейное приращение (LMO) с использованием оцененной скорости в преломляющей поверхности, третий элемент в уравнении (3.45) должен быть интерпретирован как остаточное LMO.

Поскольку уравнение (3.45) не содержит структурного элемента, любая длинноволновая статическая аномалия разделяется между элементами. Этого не происходит в случае модели остаточной статики, основанной на использовании отраженных волн [уравнение (3.25)]. Поэтому после коррекции полевой статики с целью учета изменения отметок превышения рассмотрим коррекцию остаточной статики, выполняемую в два шага:

1. 1. Коррекция статики, основанная на использовании преломленных волн с целью удаления длинноволновых аномалий.

2. 2. Коррекция остаточной статики, основанная на использовании отраженных волн с целью удаления каких-либо оставшихся коротковолновых статических смещений.

Отметим, что линейной модели времени пробега в уравнении (3.45) свойственна некоторая неопределенность величины скорости в ЗМС, как и в методе «плюс-минус» и GRM.

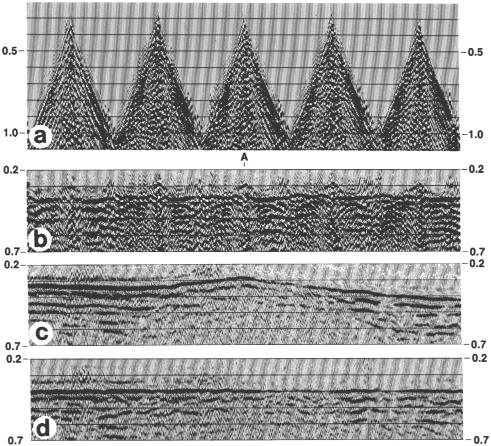
На рис.3.101 показан суммарный разрез, где применена только полевая статика. Вздутие в положении средней точки А, вероятно, связано с аномалией длинноволновой статики. Начнем с выборок ОСТ (рис.3.102а) и применим к ним поправку за линейное приращение (рис.3.102b). Предполагая, что первые вступления соответствуют преломляющей поверхности ВЧР, используем скорость, оцененную по первым вступлениям (обычно по части косы), чтобы ввести эту поправку. Суммарный разрез верхней части данных после ввода поправки за линейное приращение показан на рис.3.102с. Этот разрез эквивалентен разрезу опорной трассы, который ассоциирован с коррекцией статики, основанной на использовании отраженных волн (пример этого показан на рис.3.85). Отклонение времен пробега оценены по выборкам, исправленным за линейное приращение (рис.3.102b) и разложен на составляющие отрезки, отсекаемые продолжением годографа ПВ на оси времен, ассоциированные с точками взрыва и приема [уравнение (3.45)]. Эти отрезки используются для расчета статических поправок за точки взрыва и приема, которые затем применяются к выборкам ОСТ, показанным на рис.3.102а. На разрезе (рис.3.102с) после коррекции статики, основанной на использовании преломленных волн, можно видеть, что произошло удаление значительной части аномалии длинноволновой статики с центром в положении средней точки А (рис.3.102d). Суммарный разрез ОСТ после коррекции статики, основанной на использовании преломленных волн (рис.3.103) больше не содержит ложной структуры (сравните с рис.3.101). Эта длинноволновая аномалия не может быть удалена с помощью коррекции статики, основанной на использовании отраженных волн (рис.3.104), но она, тем не менее, удалила коротковолновые компоненты статики, присутствовавшие в данных. Объединяя две поправки, мы получаем улучшенный разрез (рис.3.105).

Рис.3.102 (а) Выборки ОСТ, взяты по профилю на рис.3.101; (b) выборки ОСТ после поправки за линейное приращение; (с) сумма выборок, исправленных за линейное приращение; (d) сумма выборок, исправленных за линейное приращение после удаления длиннопериодной статики сравните с (с).

 

Рис.3.103 Сумма ОСТ после удаления длиннопериодной статики с использованием вступлений преломленной волны (сравните с рис.3.101).

 

Рис.3.104 Сумма ОСТ после коррекции остаточной статики с использованием отраженных волн (сравните с рис.3.101).

 

Рис.3.105 Сумма ОСТ после коррекции статики с использованием преломленных и отраженных волн (сравните с рис.3.101, 3.103 и 3.104).

 

УПРАЖНЕНИЯ

 

Упражнение 3-1. Почему соль характеризуется аномально высокой скоростью (от4.5 до 5.5 км/c)?

Упражнение 3-2. Измерьте времена пробега, соответствующие выносам 1 и 3 км на рис.3.5. Затем рассчитайте скорость над отражающей поверхностью и проверьте, что она равна 2264м/с. Трасса с нулевым выносом не регистрируется, поэтому t(0) – обычно неизвестная величина.

Упражнение 3-3. Обратитесь к рис.3.25 и рассчитайте интервальные скорости между отражениями при t(0) = 0.4 и 0.8мс и при t(0) = 1.2 и 1.6с, используя метод прямого края (Clearbout?s straightedge method). Проверьте результаты, сопоставления с функцией интервальной скорости на рис.3.11.

Упражнение 3-4. Обратитесь к рис.3.8. Выборка ОСТ на рис.3.8а содержит гиперболу. Являются ли кривые гиперболическими, если ввести поправку за нормальное приращение и использовать скорости 2000 (рис.3.8b) и 2500м/с (рис.3.8с)?

Упражнение 3-5. Выполните выбор скорости из развертки постоянной скорости на рис.3.26.

Упражнение 3-6. Выполните выбор скорости из панели CVS на рис.3.27. Идентифицируйте кратные отражения.

Упражнение 3-7. Выполните выбор скорости из панели CVS на рис.3.106.

Упражнение 3-8. Выведите соотношение Levin [уравнение (3.7)] для скорости нормального приращения в случае одной наклонной отражающей поверхности (см. рис.3.16).

Упражнение 3-9. Рассмотрим два пересекающихся профиля. Ожидаете ли вы, что скоростной анализ в точке пересечения дает одну и ту же скоростную функцию?

Упражнение 3-10. Что является правильным: скоростной анализ по линии приведения или скоростной анализ по поверхности?

Упражнение 3-11. Почему уравнение (3.3) содержит элементы только с четными степенями?

Упражнение 3-12. Выведите выражение для интервальной скорости как функции среднеквадратичной скорости, используя уравнение (3.4).

Упражнение 3-13. Выведите соотношение Levin для трехмерного случая, используя геометрические построения по рси.3.17.

Упражнение 3-14. Выведите соотношение для растяжения нормального приращения, описанного уравнением (3.6).

Упражнение 3-15. Заполните пропуски в таблице. Средняя скорость v_avg, которая связывает вертикальное время пробега с глубиной в горизонтально-слоистой среде, определяется как:

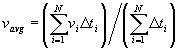
где Dt_i = Dz_i/v_i, Dz_i = мощность слоя, v_i = интервальная скорость. Среднеквадратичная скорость определяется уравнением (3.4).

Мощность слоя м	Интервальная скорость м/с	Среднеквадратичная скорость м/c	Средняя скорость м/с
		*	*
		*	*
		*	*
		*	*
		*	*

Упражнение 3-16. Объясните, почему скорость для горизонта А на рис.3.48 ведет себя так, как показано на изображении HVA под соляным куполом S. Соль является высокоскоростным слоем.

Рис.3.106 Панель CVS по профилю на площади со сложными структурами (см. упражнение 3.7).

 

Рис.3.106 продолжение

 

Рис.3.106 продолжение

 

Рис.3.106 продолжение

 

Упражнение 3-17. Предположим, что вы хотите аппроксимировать множество наблюденных времен пробега параболой вида t(x) = a + bx + cx². Входные значения приведены ниже в виде таблицы:

i	xi	t?i
		0.4 1.1 3.5 7.9 14.4

Имеются пять уравнений и три неизвестных. Поставьте задаче наименьших квадратов и решите относительно a, b, и c.

Упражнение 3-18. Решите систему

x1 – 2x2 = 1 x1 + 4x2 = 4

используя итеративный метод Гаусса-Зайделя. Проверьте результаты, решив эти уравнения методом подстановки, чтобы получить решение: х₁ = 2 и х₂ = 0.5.

Упражнение 3-19. Решите систему

x1 + 4x2 = 4 x1 – 2x2 = 1

используя итеративный метод Гаусса-Зайделя. Это такая же задача, что в упражнении 3-18, но изменен порядок уравнений. Решение должно быть таким же. Вы увидите, что решение не может быть получено, т.к. процесс итерации не сходится. Это указывает на необходимость соблюдения порядка при решении методом Гаусса-Зайделя.

Упражнение 3-20. Запишите уравнения (3.38) и (3.39) для i = 1,2,3 и j = 1,2,3. Вы увидите, что имеется шесть неизвестных при пяти независимых уравнениях.

Упражнение 3-21. Используя геометрические построения на рис.3.97, выведите выражение для глубины до коренных пород [уравнение (3.41)].

Упражнение 3-22. Используя геометрические построения на рисунке 3.98а, покажите, что время «плюс», определенное уравнением (3.43а) – это точка пересечения продолжения годографа ПВ с осью времени, а время «минус» относится к обратной величине скорости в коренных породах.

Упражнение 3-23. Можете ли вы использовать методики введения статических поправок, основанные на использовании преломленных волн на площадях с ММП?

Упражнение 3-24. Какие из перечисленных фактов оказывают неблагоприятное воздействие на качество спектра скоростей: аномалии длинноволновой или коротковолновой (меньше длины косы) статики?

Упражнение 3-25. Каким образом внутреннее обнуление выборки ОСТ влияет на спектр скоростей?