Потери при нескольких временах релаксации

Обобщим формулы для ε' и ε" на случай набора времен релаксации. Пусть f(τ) — относительная вероятность, что время релаксации равно τ. Если у всех молекул одно и то же τ, эта вероятность равна единице. При наборе времен релаксации f(τ)dτ есть вероятность того, что время релаксации лежит в интервале от τ до τ+dτ, причем

.

Интегрирование выполняется от нуля до бесконечности, так как время релаксации должно иметь какое-либо значение в этих пределах. Если же нет времен релаксации, меньших τ_a и больших τ_b, то в интеграле можно было бы в качестве пределов интегрирования взять τ_a и τ_b. Значение интеграла не изменилось бы, так как интеграл от нуля до τ_a и от τ_b до бесконечности был бы равен нулю вследствие равенства нулю вероятности f(τ) при τ < τ_a и τ > τ_b. Поэтому, принимая в качестве пределов интегрирования нуль и бесконечность, мы не изменяем значение интеграла. При учете распределения времен релаксации [см. ] выражения для ε' и ε" изменятся и запишутся следующим образом:

,

.

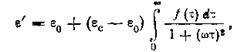В случае одного времени релаксации эти формулы принимают вид выражений .

Функцию распределения можно подобрать так, чтобы вычисленные значения соответствовали экспериментальным данным, однако при этом функция распределения может иметь сложный вид. Простые функции распределения, в частности функция распределения Гаусса, приводят к сложным зависимостям ε' и ε" от частоты, которые в некоторых случаях относительно хорошо совпадают с экспериментальными данными.

При выборе функции распределения f(τ) необходимо учитывать, что одновременно с расширением максимума в частотном ходе ε" или tgδ происходит уменьшение максимальных значений ε" и tgδ. Вследствие этого площадь S, ограниченная кривой, изображающей зависимость ε" от ln ω, и осью абсцисс, на которой отложен ln ω, не зависит от конкретного вида правильно выбранной функции распределения f(τ). На Рис. 7‑8 эта площадь заштрихована.

Рис. 7‑8. К определению функции распределения времен релаксации f (τ), которая выбирается так, чтобы заштрихованная площадь равнялась

Вычислим площадь

.

Здесь использована формула для ε" и принято во внимание, что при ω == 0. Меняя в порядок интегрирования, находим

Так как , то

.

Условие учитывается при выборе вида выражения для ε", правильно описывающего зависимость ε" от частоты в случае, когда имеется распределение времен релаксации.

7.7.3. Рассмотрим одно из выражений для ε", предложенное Фуоссом и Кирквудом. Перепишем в виде

.

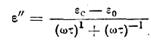Когда ωτ == 1, ε" принимает значение

.

Значение ε" в максимуме можно уменьшить, умножив правые части выражений и на λ, где 0 < λ < 1.

Выражение для ε" Фуосс и Кирквуд записывают в виде

,

здесь τ_в - наиболее вероятное время релаксации, вокруг которого группируются времена релаксации молекул,
0 < λ < 1 дает более широкий и менее высокий максимум, чем формула .

Величина ε" в максимуме при ωτ_в == 1 равна

.

Чем меньше λ, тем слабее зависимость ε" от ω, тем шире максимум в частотном ходе ε" и тем более широкая функция распределения времен релаксации f(τ). Как легко проверить, функция Фуосса и Кирквуда удовлетворяет условию .

Диаграммы Коула—Коула

Большое значение при исследовании распределения времен релаксации имеют диаграммы, предложенные братьями Коул, так называемые диаграммы Коула—Коула. На диаграммах, Коула—Коула строится зависимость ε" от ε'.

В случае одного времени релаксации эта диаграмма представляет собой полуокружность, радиус которой 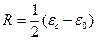и центр лежит на оси ε' на расстоянии от начала координат (Рис. 7‑9). Исследуя уравнения , видим, что при ωτ = 0 составляющие комплексной диэлектрической проницаемости ε' == ε_c и ε" == 0, и определяем соответствующую точку на окружности, лежащую на оси ε'. При эти составляющие ε' == ε₀ и ε" == 0, что дает другую точку на оси ε'. При ωτ == 1 получаем

Рис. 7‑9. Диаграмма Коула— Коула для случая, когда имеется только одно время релаксации

,

.

Уравнение окружности Коула—Коула можно записать в виде

.

Подставляя сюда значение ε' и ε" из уравнений и выбирая

,

,

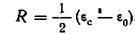Рис. 7‑10. Диаграмма Коула— Коула для случая, когда имеются два времени релаксации

можно показать, что уравнение удовлетворяется.

Если имеется несколько времен релаксации, то вид диаграмм Коула—Коула усложняется. Например, в случае двух времен релаксации на диаграмме будут две полуокружности вместо одной. Диаграмма Коула—Коула для частотной зависимости ε' и tgδ, изображенной на Рис. 7‑5, приведена на Рис. 7‑10.

Рассмотрим, как преобразуются диаграммы Коула—Коула в случае набора времен релаксации, группирующихся вокруг наиболее вероятного времени релаксации τ_в. Заметим, что выражение для комплексной диэлектрической проницаемости е* можно записать в двух эквивалентных формах:

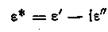
где ε' и ε" определяются уравнениями и

.

Отделяя в выражении вещественную часть от мнимой, можно показать, что оно сводится к уравнению .

Влияние распределения времен релаксации сказывается в том, что зависимость е* от ω становится меньше; это можно учесть, заменив выражение следующим:

,

где 0 < α < 1. Как вытекает из уравнения , диэлектрическая проницаемость при частоте ω == 0 равна ε_с и при ω = ¥ равна ε₀, а мнимая часть диэлектрической проницаемости пропадает.

Разделяя в вещественную и мнимую части, находим

где

,

.

При α = 0, что имеет место, когда есть только одно время релаксации, выражения и упрощаются и переходят в .

Как легко проверить, анализируя формулы и , максимальное значение ε' равно ε_с при ω = 0, минимальное значение ε' равно ε₀ при ω = ¥. Дифференцируя ε" по ωτ_в и приравнивая производную нулю, находим, что ε" проходит через максимум при ωτ_в = 1, достигая в максимуме величины

.

Очевидно, это значение меньше, чем —максимальная величина ε" при одном времени релаксации. Чем ближе α к единице, тем более размыта функция распределения времен релаксации и тем ниже величина ε" в максимуме. На плоскости ε'ε" диаграмма Коула—Коула в случае представится дугой окружности, пересекающей ось ε' в точках ε₀ и ε_c, с радиусом

,

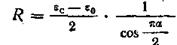и центром, лежащим ниже оси ε' на величину

.

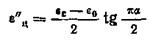Вдоль оси ε' расстояние от начала координат до центра окружности равно

Рис. 7‑11. Диаграмма Коула—Коула для случая, когда имеется набор времен релаксации

.

Диаграмма Коула — Коула для случая представлена на Рис. 7‑11. Радиус, проведенный от центра окружности О в точки ε₀ и ε_c, составляет с осью ε' углы .

Имея результаты изменений ε' и ε" при различных частотах, диаграмму Коула — Коула строят следующим образом. Значение ε' и ε" при какой-либо частоте наносят на плоскость ε'ε" в виде точки. Затем наносят точку, координаты которой равны соответствующим значениям ε' и е" при другой частоте, и т. д. По экспериментальным точкам проводится кривая, которая, как показывает опыт, является либо дугой окружности, либо наложением нескольких дуг. Построив окружности, определяют угол и параметр распределения α. Если получается несколько дуг (см. Рис. 7‑10), значит в диэлектрике действует несколько механизмов релаксации или есть несколько видов молекул с различными временами релаксации.