Построение кубического сплайна в пакете MATLAB

Function res=G(xx,x,f,M)

% исходные данные – x, f; М – значения вторых производных

n=size(x);

n=n(2);

h=zeros(1,n-1);

% вычисление шага

for i=1:n-1

h(i)=x(i+1) - x(i);

end;

for j=1:length(xx)

X=xx(j);

% определение номера интервала

for i=1:n-1

if x(i)<=X && X<x(i+1)

k=i;

break

end;

end;

% вычисление значения сплайна в промежуточной точке

yy(j)=M(k)*((x(k+1)-X)^3)/(6*h(k)) + M(k+1)*((X-x(k))^3)/(6*h(k)) +...

(f(k)-M(k)*(h(k)^2)/6)*(x(k+1)-X)/h(k)+...

(f(k+1)-M(k+1)*(h(k)^2)/6)*(X-x(k))/h(k);

end;

res=yy;

return

% вызов процедур и построение графика

>> x = [-4 -3.5 -2 0 2.1 2.5 5];

>> f=[0.5 0.2 -0.7 0 1.1 0.8 -1.6];

>> xx=linspace(-4,5,1000)

>> M = Work(x,f) % функция нахождения вторых производных

>> yy=G(xx,x,f,M);

>> plot(xx,yy,'r')

Построение кубического сплайна в пакете MATHCAD.

Задав исходные данные и определив шаг для каждого интервала, можно определить функции для формирования матриц A и H и функцию для построения кубического сплайна g(X):

 

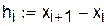
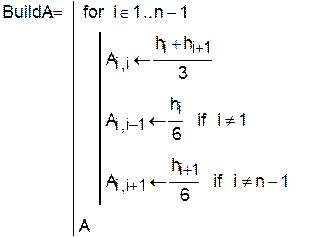
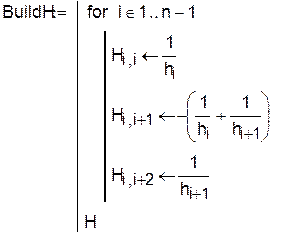
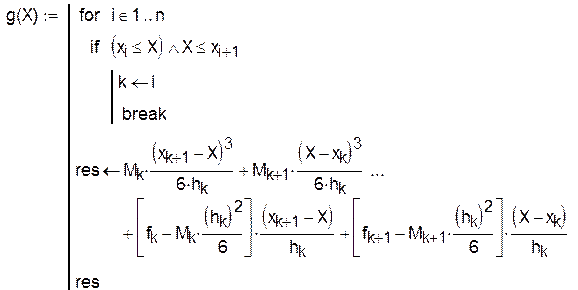
Варианты лабораторных работ

Номер варианта	Исходные данные
	x y	1,4 0,3365	1,8 0,5878	2,3 0,8329	2,9 1,0647	3,2 1,1632	3,6 1,2809
	x y	2,0 0,6931	2,5 0,9163	2,8 1,0296	3,3 1,1939	3,6 1,2809	4.0 1,3863
	x y	4,0 1,3863	4,5 1,5041	4,9 1,5892	5,4 1,6864	5,7 1,7405	6,0 1,7918
	x y	1,2 0,1823	1,6 0,4700	2,1 0,7419	2,6 0,9555	3,0 1,0986	3,3 1,1939
	x y	2,2 0,7885	2,7 0,9933	3,1 1,1314	3,6 1,2809	4,0 1,3863	4,3 1,4586
	x y	3,2 1,1632	3,6 1,2809	4,1 1,4110	4,6 1,5261	4,9 1,5892	5.4 1,6864
	x y	3,4 1,2238	3,9 1,3610	4,3 1,4586	4,9 1,5892	5,2 1,6487	5,6 1,7228
	x y	1,6 0,4700	2,1 0,7419	2,7 0,9933	3,2 1,1632	3,6 1,2809	4,1 1,4110
	x y	2,8 1,0296	3,1 1,1314	3,7 1,3083	4,2 1,4351	4,6 1,5261	5,0 1,6094
	x y	3,1 1,1314	3,6 1,2809	4,0 1,3863	4,6 1,5261	4,9 1,5892	5,3 1,6677
	x y	1,9 0,6419	2,5 0,9163	2,9 1,0647	3,4 1,2238	3,6 1,2809	4,0 1,3863
	x y	1,7 0,5306	2,2 0,7865	2,8 1,0296	3,2 1,1632	3,5 1,2528	4,0 1,3863
	x y	3,6 1,2809	4,2 1,4351	4,5 1,5041	5,2 1,6487	5,5 1,7047	5,9 1,7750

Варианты лабораторных работ (окончание)

Номер варианта	Исходные данные
	x y	3,3 1,1939	3,9 1,3610	4,4 1,4816	5,0 1,6094	5,4 1,6864	5,9 1,7750
	x y	1,1 0 ,0953	1,7 0,5306	2,4 0,8755	2,8 1,0296	3,3 1,1939	3,6 1,2809
	x y	2,1 0,4718	2,5 0,9163	3,0 1,0986	3,5 1,2528	3,8 1,3350	4,2 1,4351
	x y	3,2 1,1632	3,7 1,3083	4,3 1,4586	4,9 1,5892	5,2 1,6487	5,6 1,7228
	x y	2,7 0.9933	3,3 1,1939	3.8 1,3350	4.6 1,5261	5,0 1,6094	5,5 1,7047
	x y	1,0 0,0000	1,5 0,4055	2,1 0,7419	2,7 0,9933	3,0 1,0966	3,4 1,2238
	x y	1,4 0,3365	1,9 0,6419	2,6 0,9555	3,0 1,0986	3,3 1,1939	3,6 1,2809
	x y	3,1 1,1314	3,7 1,3083	4,2 1,4351	4.8 1,5686	5,2 1,6487	5,5 1,7047
	x y	2,6 0,9555	3,2 1,1632	4,0 1,3863	4,5 1,5041	4,9 1,5692	5,4 1,6864
	x y	1,6 0,4700	2,2 0,7885	2,7 0,9933	3,4 1,2238	3,6 1,2809	4,0 1,3836
	x y	2,1 0,7419	2,7 0,9933	3,33 1,1939	3,8 1,3350	4,0 1,3863	4,4 1,4816
	x y	2,6 0,9555	3,0 1,0986	3,9 1,3610	4,5 1,5041	4,8 1,5686	5,3 1,6677
	x y	4,5 1,5041	4,9 1,5892	5,5 1,7047	6,0 1,7918	6,2 1,8245	6,5 1,8718
	x y	3,5 1,2528	3,8 1,3350	4,5 1,5041	5,1 1,6292	5,4 1,6864	5,8 1,7579
	x y	2,8 1,0296	3,3 1,1939	3,9 1,3610	4,6 1,5261	5,0 1,6094	5,5 1,7047
	x y	4,1 1,4110	4,6 1,5261	5,2 1,6487	6,0 1,7918	6,2 1,8245	6,5 1,8718

ВСТРОЕННЫЕ ФУНКЦИИ ИНТЕРПОЛИРОВАНИЯ

Пакет MATHCAD

В MATHCAD можно использовать линейную интерполяцию, когда точки данных соединяются отрезками прямых, или кубическую сплайн-интерполяцию, когда точки соединятся отрезками кубической параболы.

Линейная интерполяция выполняется функцией linterp(vx,vy,x), которая возвращает линейно интерполируемое значение y, соответствующее третьему аргументу x. Аргументы vx,vy – это исходные векторы данных одинаковой длины, причем элементы вектора vx должны быть расположены в порядке возрастания.

Кубическая сплайн-интерполяция позволяет провести кривую через заданные точки так, чтобы первые и вторые производные были непрерывны в каждой точке. Эта кривая образуется кубическими полиномами, проходящими через наборы из трех смежных точек, которые затем состыковываются друг с другом, чтобы образовать одну кривую. Порядок выполнения такого вида интерполяции следующий:

1. Создать векторы исходных данныхvx,vy одинаковой длины, причем элементы вектора vx должны быть расположены в порядке возрастания.

2. Вычислить вектор vs , который будет содержать значения вторых производных интерполяционной кривой в заданных точках. Вектор vsможно вычислить, используя одну из функций, которые отличаются лишь граничными условиями, а именно:

· lspline(vx,vy)– генерация сплайна, который приближается к прямой линии в граничных точках;

· pspline(vx,vy)– генерация сплайна, который приближается к параболе граничных точках;

· cspline(vx,vy) – генерация сплайна, который приближается к кубической параболе в граничных точках.

3. Чтобы найти интерполируемое значение в произвольной точке, например в точке x, необходимо вычислить функцию interp(vs,vx,vy,x).

Обратите внимание, что можно сделать то же самое, вычисляя, например, interp(cspline(vx,vy),vx,vy,x). Пример сплайн-интерполяции показан на рис. 8.1.

Для узловой и промежуточной точек найдены ординаты yсоответствующих точек сплайна. Нахождение значения в узловой точке – это проверка правильности алгоритма. На рис. 8.1 также построен график интерполирующей функции и крестиками отмечены узловые точки. Для получения наилучших результатов значение x должно находиться между значениями в векторе vx.

Иногда необходимо оценить поведение функции вне отрезка, на котором заданы данные. В MATHCAD есть функция predict, которая позволяет это сделать. Эта функция использует линейный алгоритм предсказания, который бывает полезен в том случае, если экстраполируемая функция гладкая и осциллирующая, но не обязательно периодическая. Формат написания функции: predict(vy,m,n) . Возвращает n предсказанных значений, используя m последних последовательных значений вектора данных vy. Элементы вектора vy должны представлять собой значения, взятые через равные интервалы. Необходимо отметить, что задача экстраполяции хорошо решаема в случае монотонных функций, представляемых полиномом невысокой степени, а также для функций, содержащих колебательную компоненту.

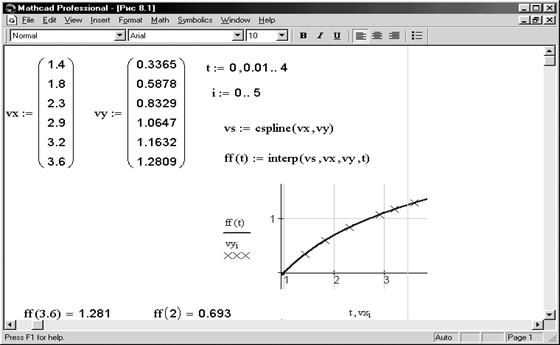
Рис. 8.1. Пример построения кубического сплайна

 

В заключение приведем список функций интерполяции и экстраполяции:

linterp (vx, vy, x);csline (vx, vy); psline (vx, vy); lsline (vx, vy); interp (vs, vx, vy, x); cspline (Mxy, Mz); pspline (Mxy, Mz);
lspline (Mxy, Mz); interp (vs, Mxy, Mz, v); predict (v, m, n).

Пакет MATLAB

Этот пакет располагает несколькими методами интерполяции и функциями, которые можно найти в каталоге polyfun.

Одномерная табличная интерполяция.Для одномерной табличной интерполяции используется функция interp1:

yi=interp1(x, y, xi, method) – возвращает вектор уi, содержащий элементы, соответствующие элементам хi и полученные интерполяцией векторов х и y. Вектор х определяет точки, в которых задано значение y. Если y – матрица, то интерполяция выполняется для каждого столбца y и уi. Параметром methodможнозадать один из следующих методов интерполяции:

• 'nearest' – ступенчатая интерполяция;

• 'linear' – линейная интерполяция (принята по умолчанию);

• 'spline' – кубическая сплайн-интерполяция;

• 'cubic' или 'pchip' – интерполяция многочленами Эрмита.

Все методы интерполяции требуют, чтобы значения х изменялись монотонно. В ряде случаев очень удобна сплайновая интерполяция таблично заданных функций, при которой промежуточные точки ищут по отрезкам полиномов третьей степени – это кубическая сплайновая интерполяция.Обычно такие полиномы вычисляются так, чтобы не только их значения совпадали с координатами узловых точек, но также чтобы в узловых точках были непрерывны производные первого и второго порядков.

Пример

Программа интерполяции функции синуса может иметь такой вид:

>>x = 0:0.2:pi; y = sin(x);

pp = interp1(x,y,'cubic','pp');

xi = 0:0.1:pi;

yi = ppval(pp,xi); % вычисляются значения интерполирующей функции

plot(x,y,'ko'), hold on, plot(xi,yi,':'), grid on, hold off

Результат представлен на рис. 8.2.

Рис. 8.2. Кубическая интерполяция синуса

 

Нетрудно заметить, что сплайн-интерполяция в данном случае дает гораздо лучшие результаты, чем линейная интерполяция. При последней точки просто соединяются друг с другом отрезками прямых, так что график интерполирующей кривой при линейной интерполяции получается негладким.

Пункт Toolsосновного меню графического окна содержит две команды:

· Basic Fitting – основные методы аппроксимации;

· Data Statistics – статистические параметры данных.

В окне Basic Fittingможно выбрать метод аппроксимации, как показано на рис 8.2 (в данном случае выбраны Spline interpolant, linear, cubic), при этом соответствующая кривая появляется в графическом окне. Активизировав параметр Show equations (показать уравнения), получим выражение аппроксимирующей функции непосредственно в графическом окне. Оценку погрешности аппроксимации можно получить, если активизировать режим Plot residuals (график погрешностей), выводящий столбцовый или линейчатый график погрешностей в узловых точках. Параметр Show norm of residuals (показать норму погрешности) позволяет вывести в окно погрешности норму, характеризующую среднеквадратичную ошибку. Чем меньше норма, тем лучше аппроксимация.

 

Рис. 8.3. Пример окна Basic Fitting

 

В рассматриваемом примере сплайн дает абсолютно точный результат, поскольку интерполяционный сплайн обязательно проходит через все узловые точки.

Команда Data Statisticsвыводит на экран окно, содержащее ряд статистических характеристик. Отметив соответствующую характеристику, можно визуализировать ее в графическом окне.