Невязки в нивелирных ходах, их допустимость и распределение

МАТЕМАТИЧЕСКАЯ ОБРАБОТКА РЕЗУЛЬТАТОВ НИВЕЛИРОВАНИЯ. НИВЕЛИРОВАНИЕ ПОВЕРХНОСТИ

6.1. Постраничный контроль

6.2. Невязки в нивелирных ходах, их допустимость и распределение

6.3. Вычисление отметок связующих и промежуточных точек. Способ превышений, способ горизонта

6.4. Построение продольного профиля трассы

6.5. Проектирование линейного сооружения

6.6. Нивелирование поверхности по квадратам

6.7. Обработка результатов нивелирования поверхности

6.8. Проведение горизонталей на плане

6.9. Точное и высокоточное нивелирование

Результаты измерения превышений методом геометрического нивелирования фиксируются в журнале технического нивелирования (табл. 6.1.). Целью обработки журнала технического нивелирования является вычисление высот определяемых точек по значениям высот исходных точек и результатам измерения превышений.

Постраничный контроль

Обработка результатов нивелирования начинается с проверки всех полевых вычислений в журнале путем постраничного контроля. Постраничный контроль заключается в выполнении следующих действий:

- вычисления суммы всех отсчетов на странице по задней рейке ;

- вычисления суммы всех отсчетов на странице по передней рейке ;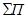

- вычисления алгебраической суммы всех средних превышений на странице ;

- проверки выполнения равенства

.

Допустимое отклонение от указанного равенства составляет 1-2 мм, которое может возникнуть вследствие накопления ошибок округлений при вычислениях средних превышений на станциях.

Перечисленные операции должны выполняться на каждой странице журнала технического нивелирования, в связи с чем такой контроль и называется постраничным. При проведении постраничного контроля проверяются только результаты полевых вычислений (отсутствие в них арифметических ошибок), качество измерений при этом не может быть проверено.

Невязки в нивелирных ходах, их допустимость и распределение

Рассмотрим разомкнутый ход нивелирования (рис.6.1). Измеренное превышение между начальной и конечной точками хода равно сумме превышений, измеренных на каждой станции, то есть

,

где - превышение, измеренное на i-ой станции. Полученное таким образом превышение между начальной и конечной точками хода называют измеренной, или практической, суммой превышений. С другой стороны, если высота H₀ начальной точки хода и высота 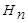конечной точки хода известны, то в соответствии с определением превышения превышение между ними может быть определено как разность их высот:

.

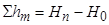Рис. 6.1. Сумма превышений

Данное значение превышения между точками A и B называют теоретической суммой превышений. Очевидно, что измеренная сумма превышений должна равняться теоретической

.

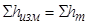Но также очевидно, что вследствие ошибок измерений такое равенство будет выполняться только тогда, когда ошибки измерений полностью компенсируются. За крайне редкими исключениями такой компенсации ошибок не будет, и сумма измеренных превышений будет отличаться от теоретической суммы превышений, то есть будет иметь место соотношение

.

Разность между измеренной суммой превышений и ее теоретическим значением называется невязкой превышений

.

(В общем случае разность между результатом измерений некоторой величины и ее теоретическим значением называется невязкой: . Пример: угловая невязка в треугольнике на плоскости есть разность между суммой его измеренных углов и 180°.)

В замкнутом нивелирном ходе отметка начальной точки равна отметке конечной точки, то есть H₀=H_n. Следовательно, теоретическая сумма превышений в замкнутом ходе равна

.

Тогда невязка в замкнутом нивелирном ходе будет равна измеренной сумме превышений, то есть

.

Очевидно, что величина невязки в нивелирном ходе будет зависеть от использованных приборов, тщательности выполненных измерений, внешних условий и ряда других факторов. При техническом нивелировании для оценки качества выполненных измерений превышений служит величина допустимой невязки, вычисляемая по эмпирической формуле

,

где L – число километров в ходе; говорят также, что L – длина хода, выраженная в километрах.

Если на каждый километр нивелирного хода приходится большое число станций (более 25), то рекомендуется использовать другую формулу:

,

где n - общее число станций в ходе.

Если полученная невязка превышений по модулю больше допустимой невязки, то есть имеет место соотношение , то результаты измерений превышений не могут быть признаны удовлетворительными, и полевые измерения должны быть выполнены повторно. Если выполняется условие , то результаты измерений считаются доброкачественными, выполненными надлежащим образом, и обработка хода может быть продолжена.

Таблица 6.1. Пример обработки журнала технического нивелирования

№ станции	№ пикетов	Отсчеты по рейкам	Превышения	Горизонт прибора	Отметки
Задняя	Перед.	Промеж.	Черн.	Красн.	Средн.	Испр.
							-3
	Рп. 1				+1208	+1210	+1209	+1206		123.456
	Х1
							-3
	Х1				+1596	+1595	+1596	+1593		124.662
	ПК0
							-3
	ПК0				-0534	-0537	-0536	-0539		126.255
	ПК1
							-3
	ПК1				-0089	-0088	-0088	-0091	126.716	125.716
	ПК2
	+25									124.928
	+41						-3			125.993
	ПК2				-1134	-1136	-1135	-1138		125.625
	ПК3
							-3
	ПК3				+2294	+2296	+2295	+2292		124.487
	Рп.2									126.779
	S						+3341	+3323
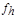
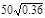
	+3340				+3323 +18	=30 мм

Но если невязка превышений допустима и не равна нулю ( ), то мы имеем определенное противоречие: измеренная сумма превышений не равна теоретической сумме превышений, чего не может быть. Поэтому полученные результаты измерения превышений нужно привести в соответствие с требованиями геометрии и здравым смыслом, “исправить” их определенным образом. В таких случаях говорят, что нужно распределить невязку, ввести в измеренные значения некоторые поправки. При этом поправки должны вводиться таким образом, чтобы сумма исправленных превышений равнялась теоретической.

Существует бесконечное число вариантов распределения поправок. При выборе такого варианта можно рассуждать следующим образом. Полевые измерения выполнялись одним и тем же прибором, по одной и той же методике, при одной и той же погоде и прочих равных условиях, поэтому у нас нет оснований одним измерениям доверять меньше и вводить в них большие поправки, а другим измерениям доверять больше и вводить в них меньшие поправки. Представляется разумным и достаточно обоснованным считать результаты наших измерений равноточными и руководствоваться при этом принципом равенства поправок. Тогда во все измерения необходимо вводить одну и ту же поправку δ, которая может быть вычислена по формуле

,

где n – число станций в ходе. При этом говорят, что поправка в превышения равна невязке с противоположным знаком, деленной на число станций. Значения поправок округляются до 1 мм.

После вычисления поправок в превышения выполняется их контроль, который сводится к проверке выполнения соотношения

,

то есть сумма поправок в превышения должна равняться невязке, взятой с противоположным знаком.

Так как при обработке результатов технического нивелирования значения превышений и поправки в превышения округляются до 1 мм, может случиться так, что вследствие ошибок округления последнее соотношение не выполняется, тогда некоторые поправки увеличивают или уменьшают на 1 мм так, чтобы выполнялось равенство . Желательно, чтобы превышения с такими поправками располагались примерно равномерно по всему ходу нивелирования.

Таким образом, можно считать, что в отдельном ходе поправки вводятся поровну во все измеренные превышения с округлением до 1 мм.