 |
Главная |
Положение и ориентация плоскостей и направлений в кристалле
|
Поможем в ✍️ написании учебной работы
|
Кристаллы – анизотропны (т. е. свойства зависят от направления).
От ориентации кристалла зависят: скорости травления, диффузии, окисления, а следовательно характеристики полупроводниковых приборов.
Для обозначения плоскостей и ориентаций в кристалле используются специальные обозначения – индексы Миллера (h, k, l).
Индексы Миллера– обратно пропорциональны длинам отрезков, отсекаемых плоскостью на осях координат.
На практике их определяют следующим образом:
- Находят точку пересечения плоскости с координатными осями;
- Измеряют длину отсечённых отрезков, используя в качестве единицы длины – постоянную решётки;
- Находят обратные величины и округляют результат до ближайших целых чисел.
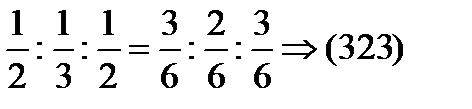 - Индексы Миллера
Направление перпендикулярное плоскости: [323].
| |
| Обозначения плоскостей и направлений: единичная плоскость – (111); - совокупность плоскостей – {111}; направление – [111]; совокупность направлений – <111>; знак минус - ставится над цифрой. |
| (010) (111) (110) |
| Рис. 1.5. Основные кристаллографические плоскости в кубическом кристалле |
Обратная решетка
Для описания электронных свойств твердых тел используют понятие обратной решетки. Обратная решетка представляет собой упорядоченную совокупность точек, представляющих безразмерные значения волнового вектора к, нормированные к импульсу частицы: k = Р/ħ. Иногда обратную решетку называют решеткой в k -пространстве или решеткой в пространстве импульсов.
Вектор трансляции обратной решётки задаётся формулой: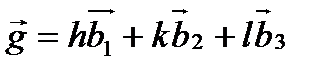 
, где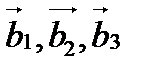 
- векторы примитивной трансляции в обратной решётке, h, k, l – целые числа. В свою очередь векторы примитивной трансляции определяются как:
; i, j, k = 1, 2, 3
- векторы примитивной трансляции решётки Браве.
Видно, что каждый из векторов обратной решетки перпендикулярен двум векторам прямой решетки. Соответственно, для кубической прямой решетки обратная решетка также кубическая. Можно показать, что гранецентрированная кубическая и объемноцентрированная решетки взаимообратны.
- объём элементарной ячейки.
: 
- волновой вектор; 
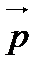- импульс электрона; h – постоянная Планка.
; 
Таким образом, обратная решетка представляет собой упорядоченную совокупность точек, представляющих безразмерные значения волнового вектора, нормированные к импульсу частицы (электрона) или квазичастицы (дырки).
Экспериментально, параметры обратной решетки находят из экспериментов по дифракции электронов.
Ячейка Вигнера-Зейтца, построенная в обратном пространстве, совпадает с первой зоной Бриллюэна (см. главу 3).
Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы