Уравнение Шредингера для кристалла

 

Возможные значения энергии электрона в кристалле можно найти из решения уравнения Шредингера для стационарных состояний, которое в общем случае имеет вид:

HY = EY, (1.31)

где H – оператор Гамильтона для кристалла, E – полная энергия кристалла, Y - волновая функция кристалла.

Волновая функция Ψ(x,t) обычно определяется из выражения для плотности вероятности нахождения частицы в точке x в момент времени t.

В общем случае волновая функция является комплексной величиной и имеет следующий вид:

(1.32)

Так как вероятность должна быть величиной действительной, то для нахождения плотности вероятности необходимо умножить Ψ(x,t) на комплексно сопряженную с ней функцию Ψ^*(x,t). Комплексно-сопряженная волновая функция:

(1.33)

Определение

Квадрат амплитуды волновой функции характеризует вероятность (P) нахождения электрона в данной точке пространства, определяемой радиус-вектором .

(1.34)

или более точно:

Квадрат модуля волновой функции, умноженный на элемент объема есть вероятность обнаружить электрон в момент времени t в объеме , образующий бесконечно малую окрестность точки .

 

Уравнение Шредингера должно быть дополнено ограничениями, накладываемыми на волновую функцию:

- волновая функция должна быть конечной (так как вероятность не может быть больше 1), однозначной (вероятность не может быть неоднозначной величиной) и непрерывной (вероятность не может изменяться скачком).

- производные ¶Y/¶x, ¶Y/¶y, ¶Y/¶z должны быть непрерывны

- функция |Y|2 должна быть интегрируема. Это условие в простейших случаях сводится к условию нормировки вероятности (т.к. электрон имеется, вероятность его существования где-то в пространстве - 100%-ная): (1.40)

Рис. 1.40. Плотность вероятности нахождения электрона в пространстве.

Твердое тело представляет собой единую систему легких (электронов) и тяжелых (ядра) частиц. Наиболее полные сведения о свойствах такой системы, в том числе и об ее энергетическом спектре, можно получить решая уравнение Шредингера, соответствующее стационарным состояниям этой системы. Но, из-за того, что в кристалле имеет место большое число взаимодействий, уравнение Шредингера приобретает сложный вид:

(1.41)

 

В уравнение (2.3) входят следующие виды энергии:

1) Кинетическая энергия электронов: , где -постоянная Дирака ( = h/2 ), m-масса электрона, а - оператор Лапласа для i-го электрона;

2) Кинетическая энергия ядер: , где -масса ядра;

3) Потенциальная энергия попарного взаимодействия электронов между собой: , где 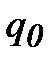-заряд электрона, здесь i ≠ j(!)

4) Потенциальная энергия попарного взаимодействия ядер между собой:

5) Потенциальная энергия взаимодействия электронов с ядрами: ,

где - координаты электронов и ядер соответственно;

6) Полная энергия кристалла E .

- собственная волновая функция кристалла, зависящая от координат всех электронов и атомных ядер.

Уравнение (21) содержит 3N(Z+1) независимых переменных, где N – число атомов в кристалле, Zq₀ – заряд ядра. Число атомов в 1 см³ составляет примерно 5*10²² и каждый атом содержит большое число электронов. Следовательно, волновая функция зависит от огромного числа (10²⁴-10²⁵) независимых переменных (в кремнии: 3N(Z+1) = 3 · 5х10²² · (14+1) = 2.25х10²⁴ переменных). Точное решение уравнения Шредингера невозможно даже для отдельных атомов, за исключением атома водорода. Поэтому задача сводится к нахождению приближений в рамках физически оправданных упрощающих предположений. Зонная теория, лежащая в основе современной физики полупроводников, базируется на следующих основных приближениях:

1.3.4. Эффективная масса носителей заряда

На свободный электрон, помещенный в однородное электрическое поле E, действует сила F=-qE, под действием которой электрон приобретает ускорение . Здесь т — масса электрона. Поскольку является единственной силой, определяющей характер движения частицы, вектор ускорения электрона направлен так же, как и вектор внешней силы, т.е. против поля E.

В кристалле, внешнее поле E действует на электрон так же, как на свободный электрон: с силой F=-qE, направленной против поля. Однако, кроме силы -qE, на электрон действуют значительные внутренние силы, создаваемые периодическим полем решетки. Это означает, что ускорение электрона в решетке в общем случае может быть не направлено параллельно внешней силе . Следовательно, движение электрона в кристалле будет более сложным, чем движение свободного электрона. Именно поэтому энергия электрона, движущегося в периодическом поле кристалла, не имеет квадратичной зависимости от волнового вектора E ≠ p²/2m. Это также следует из теоретических моделей (например, модели Кронига и Пенни). Однако для практических целей иногда удобно сохранить зависимость энергии электрона от квазиимпульса в классическом виде, а все различия, вызванные влиянием периодического поля, включить в массу электрона. Тогда формулу Е р²/2m можно переписать в виде Е=р²/2m^*, где вместо т появляется некоторая величина т*, которая является функция энергии, и которая называемая эффективной массой. Для определения понятия эффективной массы можно воспользоваться несколькими подходами.

(а) Определение эффективной массы из разложения в ряд Тейлора (формальный, математический метод). В одномерном случае величину т* можно рассчитать из разложения энергии в ряд Тейлора около экстремальных точек (т. к. E(k)- периодическая функция k и E(k)~cos(k) (периодический член))

(1.71)

Так как в точках k=k_o энергия имеет максимум или минимум (см. рис. 1.46, 1.47), то первая производная равна нулю. Ограничиваясь вторым приближением, из (1.71) находим:

(1.72)

Или: (1.73)

Если E(k)-E(k₀)=E(k₁), а k-k₀=k₁, тогда ,

Следовательно, роль эффективной массы играет величина

(1.74)

В низших точках разрешенных зон Е(k) имеет минимумы, а вторая производная от Е по k больше нуля. Поэтому на дне зоны эффективная масса положительна, а в вершинах зон отрицательна, поскольку d²E/ dk²<0. В некоторой точке в центре зоны m* ® 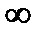. Очевидно, разложение энергии в степенной ряд (1.71) и формула (1.74) справедливы только вблизи точек экстремума.

(б) Определение эффективной массы из квазиклассического подхода.

Понятие эффективной массы имеет более широкие границы применимости и может быть введено исходя из принципа соответствия. Известно, что средние квантовомеханические величины удовлетворяют тем же соотношениям, что и соответствующие им классические величины. Так, волновые пакеты, составленные из решений уравнения Шредингера, движутся по траекто­риям классических частиц. Поэтому уравнению Ньютона должен соответствовать квантовомеханический аналог, то есть квантовомеханическое уравнение движения электрона в кристалле.

Таким образом, можно использовать квазиклассический подход (наполовину классический, наполовину квантовомеханический). В этом подходе квантовомеханическим, является определение электрона как волны. В этом случае движение электрона в кристалле можно описать с помощью волнового пакета, составленного из блоховских функций. Тогда средняя скорость движения электрона равна групповой скорости распространения всего волнового пакета - . Учитывая, что 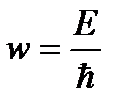, для групповой скорости получаем:

(1.75)

Аналогичным образом можно ввести усредненное ускорение волнового пакета (электрона) в кристалле:

(1.76)

С учетом того, что время и квазиимпульс независимы, в (1.76) можно поменять местами порядок их дифференцирования:

(1.77)

Классическим,в настоящем подходе,является определение работы внешней силы над рассматриваемым электроном, которая приводит к увеличению энергии (скорости) электрона:

, откуда или (1.78)

Подставляя (1.78) в (1.77) и учитывая, что внешняя сила F не зависит от k, получим:

(1.79)

Перепишем в виде: (1.80)

Т.е. по аналогии с законом Ньютона, величину можно назвать массой электрона:

(1.81)

Величина т* получила название эффективной массы электрона. Эффективная масса отражает влияние периодического потенциала решетки на движение электрона в кристалле под действием внешней силы. В периодическом поле кристаллической решетки электрон движется под действием внешней силы F в среднем так, как двигался бы свободный электрон под действием этой силы, если бы он обладал массой т* Таким образом, если электрону в кристалле вместо массы т приписать эффективную массу т*, то его можно считать свободным и движение этого электрона описывать так, как описывается движение свободного электрона, помещенного во внешнее поле. Разница между т* и m обусловлена взаимодействием электрона с периодическим полем решетки, и, приписывая электрону эффективную массу, мы учитываем это взаимодействие.

Эффективная масса, в отличие от обычной массы, не определяет ни инерционных, ни гравитационных свойств частицы. Она является лишь коэффициентом в уравнении движения и отражает меру взаимодействия электрона с кристаллической решеткой.

Пользуясь понятием эффективной массы, задачу о движении электрона в периодическом поле решетки V( ) можно свести к задаче о движении свободного электрона с массой т*. Это значит, что вместо уравнения Шредингера с периодическим потенциалом

, нужно решать уравнение

, (1.82)

Метод решения уравнения Шредингера, в котором вид периодического потенциала решетки автоматически учитывается через эффективную массу, называется методом эффективной массы

В общем случае эффективная масса является анизотропной величиной и для разных направлений волнового вектора различна. Она представляет собой тензор второго ранга:

или (1.83)

Таким образом, если зависимость [закон дисперсии] анизотропна, то эффективная масса представляет собой тензор обратных эффективных масс.

 

Рассмотрим некоторые свойства эффективной массы.

Из формул (1.74), (1.81), (1.85) следует, что эффективная масса определяется видом дисперсионной зависимости E(k). В приближении сильной связи выражение E(k) имеет вид (1.70), как это следует из модели Кронига-Пенни. Периодичность волновой функции (1.51), (1.52) и энергии электрона в кристалле (1.54) позволяет ограничиться рассмотрением зависимости E(k) в первой зоне Бриллюэна. Возьмем первую (нижнюю) ветку дисперсионной кривой E(k) в первой зоне Брилюэна для кристалла кубической сингонии (рис. 1.48а) и проведем дифференцирование. Поскольку E(k) имеет функциональную зависимость, близкую к E(k) ~ cos (ka) (см. формулу (1.70)), первая производная вблизи точек экстремума будет близкой к зависимости dE/dk ~ sin (ka). Во всей первой зоне Бриллюэна, зависимость dE/dk есть зависимость скорости электрона от волнового вектора k: (dE/dk=V_g).

Вторая производная и ее обратная зависимость (пропорциональная эффективной массе) приведены на рис. 1.48. Сравнение зависимости E(k) на рис. 1.48(а) и зависимости m*(k) на рис. 1.48(г) позволяет сделать следующие комментарии. Электрон, находящийся внутри идеальной периодической решетки может иметь как положительную, так и отрицательную эффективную массу. Если кривая на диаграмме E-k имеет выпуклость вниз (относительно оси энергий, если принять направление увеличения энергии - вверх), то масса m*>0. Если же кривая имеет выпуклость вверх (около ), тогда m*<0.

Отрицательная эффективная масса означает, что ускорение электрона направлено против действия внешней силы. Это видно из рис. 1.48б. При k, близких к границе зоны Бриллюэна, несмотря на увеличение k, скорость электрона уменьшается. Данный результат является следствием брэгговского отражения. В точке k= — состояние электрона описывается уже не бегущей, а стоячей волной и =0. В случае, когда m*<0 (на рис. 1.48(г) это области –π/a<k<π/2a и π/2a<k<π/a), частица будет ускоряться в направлении, противоположном направлению движения нормального (отрицательно заряженного) электрона; т.е. будет вести себя как некоторая гипотетическая частица, с положительным зарядом и положительной массой. Поскольку свойства электронов с отрицательной эффективной массой очень сильно отличаются от свойств "нормальных" электронов, их удобнее описывать, пользуясь представлением о некоторых квазичастицах, имеющих заряд +е, но и положительную эффективную массу. Такая, квазичастица[1] получила название дырка. Обозначение дырки – h (от англ. «hole»).

	A hν
Рис. 1.48. Зависимость энергии (а), скорости (которая ~ dE/dk) (б), величины d2E/dk2 (в) и эффективной массы (г) от волнового вектора для кубической решетки.	Рис. 1.49. Схема перемещения связанных носителей (электронов) и свободных носителей (дырок) внутри валентной зоны.

Понятие дырки поясним следующим примером (рис. 1.49):

Предположим, в исходном состоянии валентная зона полностью заполнена электронами (нет свободных энергетических уровней), а зона проводимости – свободна. Включив внешний приток энергии (нагрев, облучение светом, радиацией и др.), можно инициировать переход электронов из валентной зоны в зону проводимости. Предположим далее, что энергия фотона передаётся электрону в валентной зоне и он переходит в зону проводимости (процесс А на рис. 1.49). С точки зрения химической связи это означает повреждение (разрыв) ковалентной связи и уход электрона в свободное перемещение по кристаллу. С точки зрения зонной теории, электрон уходит в зону проводимости, а на потолке валентной зоны образуется незанятое место (квантовое состояние).

Если внешнее электрическое поле E равно нулю и вследствие того, что электроны стремятся занять самые нижние энергетические состояния, дырка занимает самое верхнее состояние (позицию 1 на рис. 1.49). Под действием электрического поля E на это незанятое состояние перейдет электрон с более низкого энергетического уровня: на рис. 1.49 это обозначено переходом электрона из позиции 2 в позицию 1. Дырка при этом опустится из позиции 1 в позицию 2. Затем этот процесс может повториться переходом (3 à 2) и т.д. по эстафете. При таком перемещении электронов, освобождающееся незанятое место на энергетическом уровне перемещается вниз, вглубь валентной зоны. Этот освобождающийся уровень и отождествляется с некоей фиктивной частицей, которая имеет равный по значению, но противоположный по знаку заряд, по сравнению с электроном. Таким образом, свободное от электрона квантовое состояние вблизи потолка валентной зоны и называют дыркой.

Важно отметить, что при переходах 1 à 2 à 3 … дырка приобретет кинетическую энергию, и полная энергия дырки возрастет (!!!), т.е. шкала энергий в валентной зоне возрастает в направлении – противоположном зоне проводимости.

Классический аналог увеличения энергии по зонам: взвешенная капля воды в воздухе (туман) – электрон в зоне проводимости, пузырек воздуха в воде – дырка в валентной зоне.

 

Таким образом, ток в кристаллах может переноситься не только электронами в зоне проводимости, но и дырками в валентной зоне. Дырочная проводимость наиболее характерна для полупроводников, однако есть и некоторые металлы, которые обладают дырочной проводимостью.

Возвращаясь к рис. 1.48в, отметим, что описывать движение электронов в кристалле, пользуясь понятием эффективной массы, можно только тогда, когда они находятся либо у дна, либо у потолка энергетической зоны. В центре зоны (около значений k = ± π/a) m*à∞, т.е. понятие эффективной массы теряет смысл. На практике почти всегда приходится иметь дело с электронами, располагающимися или у дна, или у потолка зоны. Поэтому использование эффективной массы в этих случаях вполне оправдано.

Ширина разрешенных зон растет, а запрещенных – уменьшается, с увеличением энергии (порядкового номера разрешенной зоны). Т.е. в общем случае зона проводимости, имеет большую ширину, чем валентная зона. Поскольку эффективная масса обратно пропорциональна ширине энергетической зоны, поэтому, как правило, . Следовательно, дырка и электрон проводимости отличаются не только знаком своего заряда, но имеют и разные по величине m*.

Иной результат получается, если в почти заполненной зоне имеются свободные места, то есть не все валентные связи обеспе­чены электронами. Тогда соседние электроны могут переходить на эти места, а само свободное место как бы перемеща­ется в пространстве. В энергетическом плане это соответству­ет переходу электронов с низких энергетических уровней на более высокие, а дырок с высоких уровней на более низкие.

Резюмируя полученную информацию:

1. Обозначения носителей зарядов в полупроводнике.

Электроны	n, e (negative, electrons)
Дырки	p, h (positive, holes)
Ток частично заполненной зоны может быть представлен как ток положительно заряженных частиц дырок. Заряд дырки положителен и по величине равен заряду электрона. Концентрация дырок обычно обозначается буквой р.

 

2. Три представления (определения) дырок:

(a) полноправная положительно заряженная частица, перемещающая в кристалле.

(b) отсутствие электрона в потолке валентной зоны.

(c) физическое отсутствие электрона в том месте, где он должен быть в равновесном состоянии – т.е. в составе ковалентной связи.

3. Направление энергии в зонах: зона проводимости – энергия увеличивается вверх; валентная зона – энергия увеличивается вниз.

4. Величина m* зависит от кривизны зоны (m* ~ (d²E/dk²)^-1)

5.Ширина зон увеличивается с E, а m^* обратно пропорциональна ширине энергетической зоны, à (a) зона проводимости энергетически шире, чем валентная; (b) (как правило).