 |
Главная |
Модель Кронига-Пенни (1930)
|
из
5.00
|
Связана с решением уравнения Шрёдингера для электрона в периодически меняющемся потенциале решётки.
Ограничимся одномерной моделью.

Ширина барьера - 
Высота барьера – V0
Уравнение Шрёдингера: 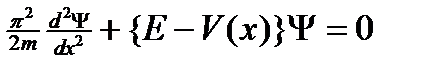 (3)
(3)
Не зависящее от времени
Решают для областей  и
и  , а затем ???? решения на границе. Решение довольно сложно и громоздко, поэтому здесь я лишь скажу, что волновую функцию можно искать в виде плоской волны
, а затем ???? решения на границе. Решение довольно сложно и громоздко, поэтому здесь я лишь скажу, что волновую функцию можно искать в виде плоской волны
(4)  , где Uk(x) - периодическая функция, период которой совпадает с периодом кристаллической решётки, тогда показать, что решение существует при условии, что E и k связаны следующим соотношением:
, где Uk(x) - периодическая функция, период которой совпадает с периодом кристаллической решётки, тогда показать, что решение существует при условии, что E и k связаны следующим соотношением:
 (5)
(5)
где физический смысл P:
(6)  1/P-характеризует прозрачность барьера (потенциального)
1/P-характеризует прозрачность барьера (потенциального)
(7) 
Т.к. левая часть уравнения (5) меняется от +1 до -1, то решение справедливо лишь при таких значениях Е, для которых правая часть этого уравнения тоже лежит в этих пределах. Построим эти кривые графически:

Вывод 1: Поскольку  и Е связаны между собой, это означает, что электрон может обладать лишь той энергией, значение которой принадлежит определённым зонам (заштрихованным) и не может иметь значения энергии вне этих зон. Иными словами существуют разрешённые и запрещённые зоны. ЭТО - основной вывод, но из уравнения (5) следуют ещё выводы:
и Е связаны между собой, это означает, что электрон может обладать лишь той энергией, значение которой принадлежит определённым зонам (заштрихованным) и не может иметь значения энергии вне этих зон. Иными словами существуют разрешённые и запрещённые зоны. ЭТО - основной вывод, но из уравнения (5) следуют ещё выводы:
Вывод 2: Если Р  , т.е. произведение
, т.е. произведение  - большое. [Физически – очень большие барьеры, т. е. атом локализуется вблизи атома, который является свободным (не взаимодействуют с другими атомами)]. – Из уравнения (5) =>
- большое. [Физически – очень большие барьеры, т. е. атом локализуется вблизи атома, который является свободным (не взаимодействуют с другими атомами)]. – Из уравнения (5) =>
 ;
; 

 сравни с потенциальной ямой.
сравни с потенциальной ямой.
Т.е. в этом случае все электроны независимы друг от друга; каждый электрон привязан к своему атому и окружён бесконечным потенциальным барьером.
Вывод 3: Р  : из (2.1)
: из (2.1)  , т.е. электрон полностью свободен.
, т.е. электрон полностью свободен.
Вывод 4: На границах разрешённой зоны cos(ka)=+,-1, т.е.  , n=1,2,3
, n=1,2,3
§2.3 Зоны Брюллеэна.
Для лучшего понимания изобразим решение в виде графика зависимости Е от k:


Т.е. точки с координатами  являются точками скачкообразного изменения энергии. Промежуток значений k между [
являются точками скачкообразного изменения энергии. Промежуток значений k между [  и
и  ]называется Зоной Брюллеэна.
]называется Зоной Брюллеэна.
Области значений k, внутри которых энергия электронов изменяется непрерывно, а на границах претерпевает разрыв, называютзоной Брюллиэна.
I зона: 
II зона:  и
и  и.т.д.
и.т.д.
Обычно рассматривают приведённую зону Брюллеэна, т.к. в кристалле существует периодичность и поэтому  ( n=0,
( n=0,  …)
…)
Легко видеть, что первая зона Брюллеэна равна элементарной ячейке в обратной решётке . По определению в обратной решётке :
 , где i, j, k=1, 2, 3.
, где i, j, k=1, 2, 3.

Для описания плоскостей и направлений в зоне Брюллеэна используют индексы Миллера.
В трёхмерном пространстве зону Брюллеэна определяют следующим образом. Через узлы обратной решётки проводят линии. Через середины таких отрезков проводят плоскости. Объёмная фигура, ограниченная такими плоскостями – есть зона Брюллеэна.
Таким образом, элементарная ячейка в обратном пространстве (в пространстве импульсов, К - пространстве) ограничивает (определяет) состояние электронов с непрерывным изменением энергетического спектра. На границах зоны Брюллеэна энергия электрона изменяется скачками.
Внутри зоны Брюллеэна (около  ) энергия электрона равна:
) энергия электрона равна: 
Снаружи: 
Энергия электрона не может принимать промежуточные значения, т.е. существует запрещённая зона. Поскольку величина вектора  зависит от направления в кристаллической. решетке, поэтому вид энергетических зависимостей
зависит от направления в кристаллической. решетке, поэтому вид энергетических зависимостей  зависит от направления! Откуда следует, что структура энергетических зон в кристалле является достаточно сложной.
зависит от направления! Откуда следует, что структура энергетических зон в кристалле является достаточно сложной.
ЭФФЕКТИВНАЯ МАССА.
ЗОННАЯ СТРУКТУРА НЕКОТОРЫХ ПРОВОДНИКОВ.
ОСНОВНЫЕ ХАРАКТЕРИСТИКИ
1)Ширина запрещенной зоны.
2)Радиус запрещенной зоны.
3)Несимметричность зоны в различных направлениях => зависимость подвижности от направления в кристаллической решетке.
|
из
5.00
|
Обсуждение в статье: Модель Кронига-Пенни (1930) |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

