 |
Главная |
Радикальный признак Коши
|
из
5.00
|
Теорема Если для ряда с положительными членами 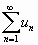 величина
величина 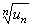 имеет конечный предел
имеет конечный предел
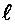 при
при 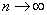 , т.е.
, т.е.
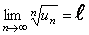 ,
,
то 1) при 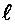 < 1 – ряд сходится;
< 1 – ряд сходится;
2) при 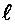 > 1 – ряд расходится.
> 1 – ряд расходится.
Замечание. Как и в признаке Даламбера, случай 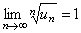 , требует дополнительного исследования. Среди рядов, удовлетворяющих этому условию, могут встретиться как сходящиеся, так и расходящиеся. Так для гармонического ряда имеем:
, требует дополнительного исследования. Среди рядов, удовлетворяющих этому условию, могут встретиться как сходящиеся, так и расходящиеся. Так для гармонического ряда имеем: 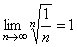 , но он расходится. Рассмотрим другой числовой ряд
, но он расходится. Рассмотрим другой числовой ряд 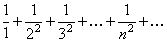 . Для него так же имеет место равенство
. Для него так же имеет место равенство 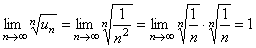 , но он сходится по первому признаку сходимости. Заметим, что если отбросить первый член, то члены оставшегося ряда будут меньше соответствующих членов ряда
, но он сходится по первому признаку сходимости. Заметим, что если отбросить первый член, то члены оставшегося ряда будут меньше соответствующих членов ряда 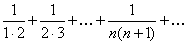 , который сходится.
, который сходится.
Интегральный признак Коши
Теорема Пусть дан ряд  , члены которого положительны и не возрастают, т.е.
, члены которого положительны и не возрастают, т.е. 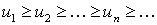 , а функция
, а функция 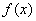 , определена при
, определена при 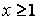 , непрерывная и не возрастающая и
, непрерывная и не возрастающая и 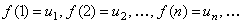 . Тогда для сходимости ряда
. Тогда для сходимости ряда  необходимо и достаточно, чтобы сходился несобственный интеграл
необходимо и достаточно, чтобы сходился несобственный интеграл 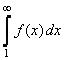 .
.
Знакопеременные числовые ряды. Абсолютная и условная сходимость.
Числовой ряд  называется знакопеременным, если среди его членов имеются как положительные, так и отрицательные числа. Знакочередующийся ряд
называется знакопеременным, если среди его членов имеются как положительные, так и отрицательные числа. Знакочередующийся ряд 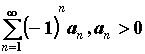 является частным случаем знакопеременных рядов.
является частным случаем знакопеременных рядов.
Теорема 1. Если знакопеременный ряд u₁+ u₂+…+ un + … (1) таков, что ряд, составленный из абсолютных величин его членов, | u₁|+ |u₂|+…+ |un | +… (2) сходится, то и данный знакопеременный ряд также сходится.
Док-во: Пусть Sn и σn—суммы n первых членов рядов (1) и (2).
Пусть далее Snʹ —сумма всех положительных, a Sn ʺ—сумма абсолютных величин всех отрицательных членов среди первых nчленов данного ряда; тогда Sn = Snʹ - Sn ʺ, σn = Snʹ + Sn ʺ
По условию, σnимеет предел σ; SnʹиSn ʺположительные возрастающие величины, меньшие σ. Следовательно, они имеют пределы Sʹ и Sʺ. Из соотношения Sn = Snʹ - Sn ʺследует, что и Snимеет
предел и этот предел равен Sʹ - Sʺ, т. е. знакопеременный ряд (1) сходится.
Опр. Знакопеременный ряд 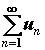 называется абсолютно сходящимся, если сходится ряд
называется абсолютно сходящимся, если сходится ряд 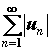 .
.
Если ряд 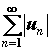 , а сам ряд
, а сам ряд 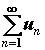 сходится, то его называют условно сходящимся.
сходится, то его называют условно сходящимся.
Теорема 2. Если ряд сходится абсолютно, то он остается абсолютно сходящимся при любой перестановке его членов. При этом сумма ряда не зависит от порядка его членов. (Это свойство не сохраняется для условно сходящихся рядов)
Теорема 3. Если ряд сходится условно, то, какое бы мы ни задали число А, можно так переставить члены этого ряда, чтобы его сумма оказалась в точности равной А. Более того,можно так переставить члены условно сходящегося ряда, чтобы ряд, полученный после перестановки, оказался расходящимся.
|
из
5.00
|
Обсуждение в статье: Радикальный признак Коши |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

