Действие над комплексными числами в тригонометрической форме, возведение в степень и извлечение корня n-ой степени из комплексного числа. Формула Эйлера

Комплексные числа и действия над ними. Изображение комплексных чисел на комплексной плоскости. Тригонометрическая форма комплексного числа.

Комплексные числа.

Определение. Комплексным числом zназывается выражение , где a и b – действительные числа, i – мнимая единица, которая определяется соотношением:

При этом число a называется действительной частью числа z (a = Re z), а b- мнимой частью (b = Im z).

Если a =Re z =0, то число z будет чисто мнимым, если b = Im z = 0, то число z будет действительным.

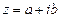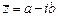Определение. Числа и называются комплексно – сопряженными.

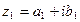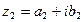Определение. Два комплексных числа и называются равными, если соответственно равны их действительные и мнимые части:

Определение. Комплексное число равно нулю, если соответственно равны нулю действительная и мнимая части.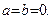

Понятие комплексного числа имеет геометрическое истолкование. Множество комплексных чисел является расширением множества действительных чисел за счет включения множества мнимых чисел. Комплексные числа включают в себя все множества чисел, которые изучались ранее. Так натуральные, целые, рациональные, иррациональные, действительные числа являются, вообще говоря, частными случаями комплексных чисел.

Если любое действительное число может быть геометрически представлено в виде точки на числовой прямой, то комплексное число представляется точкой на плоскости, координатами которой будут соответственно действительная и мнимая части комплексного числа. При этом горизонтальная ось будет являться действительной числовой осью, а вертикальная - мнимой осью.

 

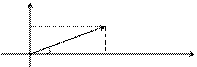у

 

A(a, b)

 

r b

j

0 a x

 

Таким образом, на оси ОХ располагаются действительные числа, а на оси ОY – чисто мнимые.

С помощью подобного геометрического представления можно представлять числа в так называемой тригонометрической форме.

Тригонометрическая форма числа.

Из геометрических соображений видно, что 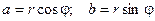. Тогда комплексное число можно представить в виде: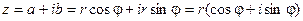

Такая форма записи называется тригонометрической формой записи комплексного числа.

При этом величина r называется модулемкомплексного числа, а угол наклона j -аргументомкомплексного числа. .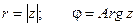

Из геометрических соображений видно:

Очевидно, что комплексно – сопряженные числа имеют одинаковые модули и противоположные аргументы.

 

Действие над комплексными числами в тригонометрической форме, возведение в степень и извлечение корня n-ой степени из комплексного числа. Формула Эйлера.

Действия с комплексными числами.

Основные действия с комплексными числами вытекают из действий с многочленами.

1) Сложение и вычитание.

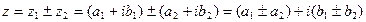
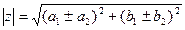
2) Умножение.

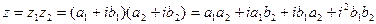
В тригонометрической форме: ,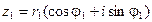

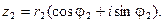
С случае комплексно – сопряженных чисел:

3) Деление.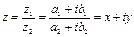

 

 

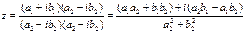
В тригонометрической форме: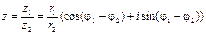

4) Возведение в степень.

Из операции умножения комплексных чисел следует, что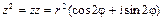

В общем случае получим: ,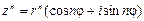

где n – целое положительное число.

Это выражение называется формулой Муавра.

Формулу Муавра можно использовать для нахождения тригонометрических функций двойного, тройного и т.д. углов.

5) Извлечение корня из комплексного числа.

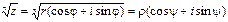
Возводя в степень, получим:

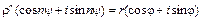
Отсюда:

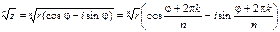
Таким образом, корень n – ой степени из комплексного числа имеет n различных значений.

3.Показательная форма комплексного числа. Действия над комплексными числами в показательной форме.
Показательная форма комплексного числа.

Рассмотрим показательную функцию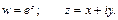

Можно показать, что функция w может быть записана в виде: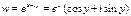

Данное равенство называется уравнением Эйлера.Вывод этого уравнения будет рассмотрен позднее. (См. ).

Для комплексных чисел будут справедливы следующие свойства:

1)

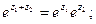
2)

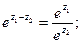
3) 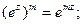где m – целое число.

Если в уравнении Эйлера показатель степени принять за чисто мнимое число (х=0), то получаем:

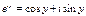
Для комплексно – сопряженного числа получаем: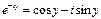

Из этих двух уравнений получаем:

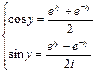
Этими формулами пользуются для нахождения значений степеней тригонометрических функций через функции кратных углов.

Если представить комплексное число в тригонометрической форме: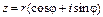

и воспользуемся формулой Эйлера: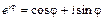

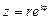
Полученное равенство и есть показательная форма комплексного числа.

4.Векторные функции скалярного аргумента. Предел, непрерывность, производная..

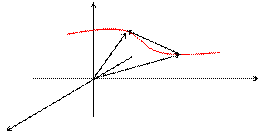z

 

A(x, y, z)

 

 

 

х

Пусть некоторая кривая в пространстве задана параметрически:

x = j(t); y = y(t); z = f(t);

Радиус- вектор произвольной точки кривой: .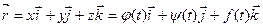

Таким образом, радиус- вектор точки кривой может рассматриваться как некоторая векторная функция скалярного аргумента t. При изменении параметра t изменяется величина и направление вектора .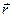

Запишем соотношения для некоторой точки t₀:

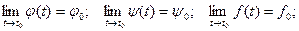
Тогда вектор 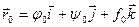- предел функции 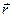(t). .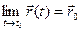

Очевидно, что

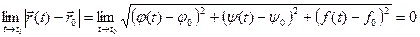, тогда

.

Чтобы найти производную векторной функции скалярного аргумента, рассмотрим приращение радиус- вектора при некотором приращении параметра t.

 

; ;

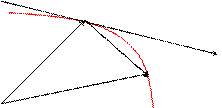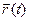
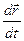
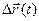
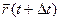
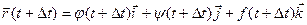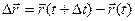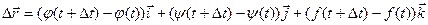
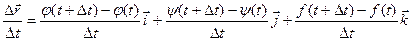
или, если существуют производные j¢(t), y¢(t), f¢(t), то

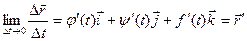
Это выражение – вектор производная вектора .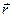

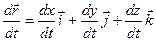
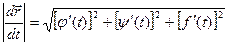
Если имеется уравнение кривой:

x = j(t); y = y(t); z = f(t);

то в произвольной точке кривой А(x_А, y_А, z_А) с радиус- вектором

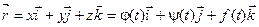
можно провести прямую с уравнением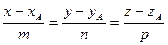

Т.к. производная 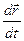- вектор, направленный по касательной к кривой, то

.

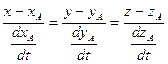Свойства производной векторной функции скалярного аргумента.

1)

2) , где l = l(t) – скалярная функция

3)

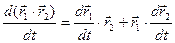
4)

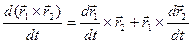
Определение. Векторной функцией действительного аргумента называется правило, которое каждому действительному числу 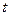ставит в соответствие единственный определенный вектор.