 |
Главная |
ПОНЯТИЕ МАТРИЦЫ. ВИДЫ ЗАПИСИ
|
из
5.00
|
Матрицы служат для представления числовых данных в удобной для матричной обработки форме. Одно из преимуществ матричной записи состоит в том, что в малом наборе символов «спрессовано» множество математических операций. Благодаря этому матричная форма записи чрезвычайно удобна при анализе данных, а необходимость в этом возникает всё чаще в связи с распространением количественных методов исследования в экономической теории и коммерческой деятельности. Матричная форма записи полезна, когда приходится прибегать к математическим методам исследования, она облегчает организацию необходимых расчётов и понимания смысла этих операций. Экономисту и менеджеру на современном этапе не обойтись без матриц и матричной алгебры.
Пример 1: Менеджер Скворцов для большей наглядности итоговых результатов приводит таблицу:
Средние розничные цены на автомобили Таблица 1.
в зависимости от срока их службы (тыс.руб.)
| Продолжительность службы (годы) | годы | ||
Можно извлечь из таблицы ряды приведенных в ней чисел и записать в форме:  ,
,
где содержательное значение каждого показателя определяется его местом в данном массиве. Числа в строке характеризуют цены автомобилей, прослуживших один и тот же срок, а в столбце – цены автомобилей различного срока службы в данном году.
Например, число 160 в третьей строке и втором столбце, представляет собой цену прослужившего 3 года автомобиля в 2005 году. Числа, записанные в строку, характеризуют цены автомобилей прослуживших один и тот же срок в различные годы, а числа в столбце – цены автомобилей, различного срока службы в данном году.
Для того, чтобы указать, что данный массив – матрица, его заключают в квадратные скобки  , или круглые
, или круглые  , или двойные вертикальные
, или двойные вертикальные  .
.
Каждое число массива называется элементом матрицы. Матричная алгебра, или алгебра матриц, изучает алгебраические операции над числовыми массивами.
Матрицу, как массив чисел, можно рассматривать как самостоятельное единое целое, поэтому можно назвать А, например:
 или
или  .
.
Исчерпав все буквы от a до z можно обозначить только 26 – элементов.
 .
.
 Читается «а – один», «а – два», «а – три». Цифры 1, 2, 3 называют индексами, которые обозначают номер столбца. Все элементы одного столбца имеют общий индекс, что на практике не удобно.
Читается «а – один», «а – два», «а – три». Цифры 1, 2, 3 называют индексами, которые обозначают номер столбца. Все элементы одного столбца имеют общий индекс, что на практике не удобно.
Обычно, на практике для обозначения элементов, используют одну букву алфавита и два индекса, записываемые рядом, первый из них обозначает строку, а второй – столбец, которым принадлежит данный элемент матрицы.
Матрицу А можно записать в виде  .
.
Элементы читаются «а один, один», «а один, два», «а один, три», и т.д. Таким образом, индексы элементов однозначно определяют место, занимаемое ими в матрице. Элемент а 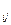 находится в i-той строке и j-ом столбце, т.е. на пересечении i-той строки j-ого столбца. Запятая между индексами ставится тогда, когда она необходима.
находится в i-той строке и j-ом столбце, т.е. на пересечении i-той строки j-ого столбца. Запятая между индексами ставится тогда, когда она необходима.
Например, а  - элемент на пересечении 4-ой строки и 13-ого столбца. Читается «а четыре, тринадцать».
- элемент на пересечении 4-ой строки и 13-ого столбца. Читается «а четыре, тринадцать».
Возможны обозначения элементов, например первой строки  в следующем виде
в следующем виде  при j=1,2,3. Таким же образом могут быть записаны и столбцы. Для обозначения всей матрицы, а
при j=1,2,3. Таким же образом могут быть записаны и столбцы. Для обозначения всей матрицы, а 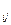 заключают в фигурные скобки
заключают в фигурные скобки  при i=1,2,3 и j=1,2
при i=1,2,3 и j=1,2
Такое обозначение полностью характеризует элементы матрицы. В общем случае  при i=1,2,…,m и j=1,2,…,n.
при i=1,2,…,m и j=1,2,…,n.
Таким образом, матрицейназывается прямоугольная таблица чисел, содержащая m-строк и n-столбцов. Матрица в общем виде записывается
А=  ,
,
Матрицу А называют матрицей размера m  n и пишут А
n и пишут А  . Числа аij - элементы матрицы.
. Числа аij - элементы матрицы.
КЛАССИФИКАЦИЯ МАТРИЦ.
Существует несколько различных обозначений операций суммирования:
 ;
;  .
.
Суммирование по i при j=2:  .
.
Суммирование по j при i=4:  .
.
Часто возникает необходимость в «двойном сложении».
 .
.
Аналогично

При двойном суммировании порядок записи слагаемых несущественен, т.е.  .
.
Обе величины равны полной сумме всех элементов матрицы.
Если в матрице число строк равно числу столбцов (m=n), то такая матрица называется квадратной.
А=  - квадратная матрица 2-го порядка
- квадратная матрица 2-го порядка
А число её строк или столбцов называется порядком матрицы. Элементы стоящие, на диагонали, идущей из верхнего левого угла, образуют главную диагональ.
Замечание:
1. Следует иметь ввиду, что в качестве индекса может служить любая буква алфавита.
2.  .
.
3.  ij-ый элемент матрицы.
ij-ый элемент матрицы.
4. 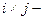 размерность матрицы (порядок матрицы, если она квадратная).
размерность матрицы (порядок матрицы, если она квадратная).
5.  - ведущий элемент матрицы.
- ведущий элемент матрицы.
 - диагональные элементы матрицы.
- диагональные элементы матрицы.
Сумма диагональных элементов квадратной матрицы называется следом матрицы и обозначается  .
.
Квадратная матрица называется треугольной, если все элементы, расположенные по одну сторону от главной диагонали, равны нулю.
Квадратная матрица, все элементы которой под диагональю равны нулю, называется верхней треугольной матрицей, а над диагональю – нижней треугольной.
 - верхняя треугольная,
- верхняя треугольная,  - нижняя треугольная матрица.
- нижняя треугольная матрица.
Матрицы, называются равными, если они одинакового размера (т.е. имеют одинаковое число строк и одинаковое число столбцов) и их соответствующие элементы равны, т.е. А=В, если аij=bij.
Квадратная матрица, у которой все элементы, кроме элементов главной диагонали, равны нулю, называется диагональной.
 - диагональная матрица.
- диагональная матрица.
Диагональная матрица, у которой каждый элемент главной диагонали равен единице, называется единичной.Обозначается буквой Е. Еn  n=
n= 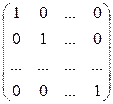 -единичная матрица n-го порядка.
-единичная матрица n-го порядка.
Матрица, все элементы которой равны нулю, называется нулевой. Обозначается буквой О.
Матрица, содержащая один столбец или одну строку, называетсяматрица-столбец, или матрица-строка соответственно. Записываются в виде
А=  , В=
, В=  .
.
Матрица размера 1  1, состоящая из одного числа, отождествляется с этим числом, т.е. (2) есть 2.
1, состоящая из одного числа, отождествляется с этим числом, т.е. (2) есть 2.
Матрица, полученная из данной путём замены каждой её строки столбцом с тем же номером, называется матрицей транспонированной к данной. Обозначается АТ.
Матрица, элементы которой симметричны относительно главной диагонали, называется симметричной.
|
из
5.00
|
Обсуждение в статье: ПОНЯТИЕ МАТРИЦЫ. ВИДЫ ЗАПИСИ |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

