Определители 3-го порядка

Рассмотрим квадратную матрицу 3-го порядка

.

Определителем 3-го порядка, соответствующим матрице А, называется число

.

Данное правило вычисления определителя 3-го порядка называется правилом треугольников или правилом Саррюса, которое символически можно записать так:

.

Определители n-го порядка.

Пусть дана квадратная матрица n-го порядка

А= .

Определители n-го порядка, соответствующий матрице А обозначается

.

Минором М_ij элемента а_ij определителя называется определитель (n-1)-го порядка, который получается из определителя путём вычёркивания i-строки и j-столбца.

Алгебраическим дополнением (адъюнктом) элемента а_ij определителя называется произведение минора М_ij этого элемента на множитель (-1)^i+j.

Определители n-го порядка (n ) называется число = , где а_ij-элемент i-ой строки, А_ij- алгебраическое дополнение этого элемента (i= ).

Свойства определителей

1. («Равноправность строк и столбцов»). Определитель не изменится, если его строки заменить столбцами, и наоборот, т.е.:

В дальнейшем строки и столбцы будем просто называть рядами определителя.

2. При перестановке двух параллельных рядов определитель меняет знак.

3. Определитель, имеющий два одинаковых ряда, равен нулю.

4. Общий множитель элементов какого-либо ряда определителя можно вынести за знак определителя.

Из свойств 3 и 4 следует, что если все элементы некоторого ряда пропорциональны соответствующим элементам параллельного ряда, то такой определитель равен нулю.

5. Если элементы какого-либо ряда определителя представляют собой суммы двух слагаемых, то определитель может быть разложен на сумму двух соответствующих определителей.

6. («Элементарные преобразования определителя»). Определитель не изменится, если к элементам одного ряда прибавить соответствующие элементы параллельного ряда, умноженные на одно и тоже любое число.

7. («Разложение определителя по элементам некоторого ряда»). Определитель равен сумме произведений элементов некоторого ряда на соответствующие им алгебраические дополнения.

8. Сумма произведений элементов какого-либо ряда определителя на алгебраические дополнения соответствующих элементов параллельного ряда равна нулю.

НЕВЫРОЖДЕННЫЕ МАТРИЦЫ.

ОБРАТНАЯ МАТРИЦА.

Пусть А – квадратная матрица n-го порядка

А= .

Квадратная матрица А называется невырожденной, если определитель не равен нулю, в противном случае ( ) матрица А называется вырожденной.

Матрицей, союзной к матрице А, называется матрица

А =

где А 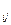- алгебраическое дополнение элемента 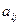данной матрицы А (оно определяется так же, как и алгебраическое дополнение элемента определителя).

Обратная матрица

Понятие обратной матрицы вводится только для квадратной матрицы.

Матрица называется обратной матрице А, если выполняется условие

,

где Е – единичная матрица того же порядка, что и матрица А. Матрица имеет те же размеры, что и матрица А.

Теорема1: Всякая невырожденная матрица имеет обратную.

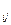Теорема2: Матрица где А - алгебраическое дополнение элемента 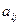невырожденной матрицы А, является обратной для матрицы А.

Алгоритм нахождения обратной матрицы.

1. Найти определитель матрицы А.

2. Найти алгебраические дополнения А 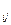всех элементов матрицы А и составить матрицу А , элементами которой являются алгебраические дополнения А .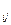

3. Найти матрицу, транспонированную полученной матрице А , и умножить её на - это и будет = .

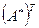4. Сделать проверку: .