 |
Главная |
Проверка гипотезы о законе распределения случайной величины по данным опыта
|
из
5.00
|
Пусть с испытанием связана случайная величина  с неизвестным законом распределения и пусть по некоторым соображениям выдвинута гипотеза Н:
с неизвестным законом распределения и пусть по некоторым соображениям выдвинута гипотеза Н:  имеет закон распределения
имеет закон распределения  , где
, где  – неизвестные параметры.
– неизвестные параметры.
Например, пусть гипотеза Н состоит в том, что случайная величина  нормальна:
нормальна:
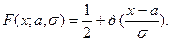
Укажем правило проверки гипотезы о законе распределения, принадлежащее Пирсону. Для этого построим критерий  , т.е. такую статистику, для которой закон распределения известен при условии, что исходная гипотеза верна.
, т.е. такую статистику, для которой закон распределения известен при условии, что исходная гипотеза верна.
1 2 … m



 1.
1.


Разделим отрезок  на m интервалов одинаковой длины
на m интервалов одинаковой длины  . Обозначим
. Обозначим  - частоты попадания элементов выборки в эти интервалы.
- частоты попадания элементов выборки в эти интервалы.
2.Обозначим 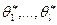 - состоятельные оценки неизвестных параметров
- состоятельные оценки неизвестных параметров  . Тогда гипотетическая функция распределения случайной величины имеет вид:
. Тогда гипотетическая функция распределения случайной величины имеет вид:
 . (47)
. (47)
3.Вычислим вероятности  попадания
попадания  в эти интервалы по формуле:
в эти интервалы по формуле:
 ,
,
где F(x) – функция (47).
4.Построим статистику Z по формуле:
 . (48)
. (48)
Критерий (48) был построен Пирсоном.
Теорема. Если гипотеза Н верна, то при достаточно большом объеме выборки случайная величина (48) подчинена приближенно закону распределения Пирсона  с
с  степенями свободы.
степенями свободы.
Из этой теоремы и указанной выше схемы проверки гипотезы вытекает следующее правило проверки гипотезы о законе распределения:
1. Задаются уровнем значимости  и вычисляют квантиль
и вычисляют квантиль  .
.
2. Выполняют выборку  и по формуле (48) вычисляют
и по формуле (48) вычисляют 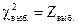 .
.
3. Если
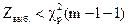 , гипотеза принимается.
, гипотеза принимается.
Если
 , гипотеза отвергается.
, гипотеза отвергается.
Ошибки первого и второго рода. Мощность критерия
При проверке гипотез по указанному правилу возможны ошибки двух типов:
1. Ошибка первого рода: отвергается верная гипотеза. Вероятность этой ошибки равна уровню значимости a. Действительно, из определения a имеем:
 Р (ошибки 1-го рода)=
Р (ошибки 1-го рода)= 
2. Ошибка второго рода: принимается неверная гипотеза. Вероятность этой ошибки обозначают b:
Р (ошибки второго рода)= 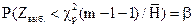 .
.
В конкретной ситуации эта вероятность может быть вычислена.
В математической статистике доказывается: при фиксированном объеме выборки уменьшение уровня значимости a влечет увеличение b и обратно, уменьшение b влечет увеличение a.
Единственный способ уменьшения одновременно a и b- это увеличение объема выборки.
В конкретных ситуациях можно минимизировать вероятность той ошибки, которая ведет к менее тяжелым последствиям. Рекомендуется, если это возможно, проводить проверку более одного раза (набрать хотя бы еще одну выборку).
3. Мощностью критерия называется вероятность отвергнуть неверную гипотезу:
 ,где
,где
b - вероятность ошибки второго рода.
|
из
5.00
|
Обсуждение в статье: Проверка гипотезы о законе распределения случайной величины по данным опыта |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

