Состоятельные несмещенные оценки для математического ожидания, дисперсии, ковариации

Пусть с испытанием связана случайная величина с неизвестными числовыми характеристиками (а, D) и пусть набрана независимая выборка (40).

В дальнейшем будем употреблять следующий удобный термин: любую функцию от выборки (40) будем называть статистикой.

Лемма 1. Статистика

(42)

является состоятельной несмещенной оценкой математического ожидания а.

Доказательство. 1. Мы знаем, что элементы выборки (40) являются независимыми случайными величинами с одним и тем же законом распределения, совпадающим с законом распределения случайной величины , а значит, имеют те же числовые характеристики (а, D).

По теореме Чебышева среднее арифметическое независимых случайных величин с одинаковыми параметрами (а, D), при неограниченном возрастании числа слагаемых сходится по вероятности к общему математическому ожиданию

что и означает состоятельность оценки.

2. Имеем

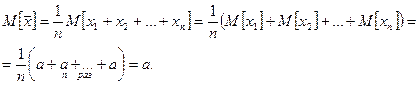
Это означает несмещенность оценки .

Лемма 2.Статистика

(43)

является состоятельной несмещенной оценкой дисперсии D. Доказывается аналогично лемме 1.

Замечание 1. Если в формуле (43) заменить (n - 1) на n , то оценка останется состоятельной, но будет смещенной. Величина S² называется исправленной дисперсией.

Замечание 2. Из леммы 2 следует, что статистика:

является состоятельной оценкой для СКО ). Можно доказать, что , т.е. оценка S является смещенной оценкой для .

Пусть по данным опыта получим ряд значений случайной точки ( ) (выборка):

(х₁, у₁) (х₂, у₂), …, (х_n, у_n).

Справедлива следующая

Лемма 3.Состоятельной несмещенной оценкой для cov( ) является выборочная ковариация

где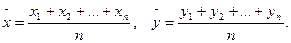

Два распределения, связанные с нормальным законом

Сформируем два результата, которые понадобятся далее.

Теорема 1.Пусть случайные величины независимы и нормальны с параметрами (0,1), тогда случайная величина подчинена закону распределения с плотностью вероятности

Рис.30

– распределение (Пирсона)

Теорема 2. Пусть случайные величины независимы и нормальны с параметрами (0,1), тогда случайная величина

подчинена закону распределения с плотностью

рис.31

T – распределение (Стьюдента)

В обоих случаях константа С подобрана так, чтобы площадь под графиком плотности была равна 1.

Число n называется числом степеней свободы.

Квантиль распределения

Пусть имеется случайная величина с функцией распределения F(x). Будем предполагать, что функция F(x) непрерывна и строго монотонна.

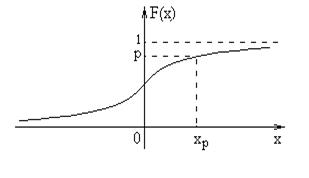
Рис.32

Зададимся числом pÎ (0,1).

Квантилем уровня p распределения F(x)называется корень уравнения F(x) = p, х - ?

Обозначим его (см. рис.32). Из определения функции F(x) вытекает: .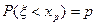

Нам понадобится далее квантили распределений Пирсона и Стьюдента. Они обозначаются:

,

Для этих квантилей имеются таблицы.