 |
Главная |
Доверительные интервалы для математического ожидания и дисперсии
|
из
5.00
|
Пусть с испытанием связана случайная величина  с неизвестными числовыми характеристиками (а, D) и пусть по выборке (40) вычислены оценки
с неизвестными числовыми характеристиками (а, D) и пусть по выборке (40) вычислены оценки 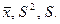
Зададимся числом р в интервале (0,1).
Теорема. В указанной ситуации при достаточно большом объеме выборки с вероятностью р имеют место неравенства
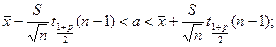 (44)
(44)
 . (45)
. (45)
Интервалы (44), (45) называются доверительными интервалами для математического ожидания и дисперсии. Число р называется уровнем доверия или доверительной вероятностью.
Здесь n-объем выборки,  -квантили распреде-лений Пирсона и Стьюдента.
-квантили распреде-лений Пирсона и Стьюдента.
Указанные интервалы иногда называют интервальными оценками для математического ожидания и дисперсии.
Пример. Выполнена выборка значений случайной величины  объема n = 25 и вычислены состоятельные несмещенные оценки для математического ожидания и
объема n = 25 и вычислены состоятельные несмещенные оценки для математического ожидания и
дисперсии:  Найти доверительные интервалы для математического ожидания и дисперсии с уровнем доверия р = 0,95.
Найти доверительные интервалы для математического ожидания и дисперсии с уровнем доверия р = 0,95.
В силу неравенств (44), (45) с р = 0,95 имеют место интервальные оценки:
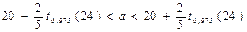 ;
;
 .
.
По таблице квантилей (IV, V) найдем:
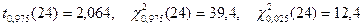 .
.
Подставляя эти значения, получим: с вероятностью 0,95 верны неравенства:
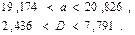
Общая схема проверки гипотез по данным опыта
Пусть исследователем выдвинута по некоторым соображениям гипотеза Н и требуется проверить справедливость этой гипотезы по данным опыта.
Укажем правило (схему) проверки гипотезы, разработанную в математической статистике.
Пусть построена статистика (функция от выборки)  со следующим свойством: если гипотеза Н верна, то известен закон распределения случайной величины Z.
со следующим свойством: если гипотеза Н верна, то известен закон распределения случайной величины Z.
1. Задаются малым числом  , (например, a = 0,01 или a = 0,05) и находят множество V значений случайной величины Z такое, что
, (например, a = 0,01 или a = 0,05) и находят множество V значений случайной величины Z такое, что
 . (46)
. (46)

 Z
Z
 V
V
2. Производят выборку  и вычисляют значение Z по этой выборке. Обозначим его
и вычисляют значение Z по этой выборке. Обозначим его  .
.
Возможны два случая:
|
|
 .
. 






 V
V  V
V
Гипотеза отвергается Гипотеза принимается
Комментарии: В первом случае гипотеза не согласуется с данными опыта, т.к. при этой гипотезе вероятность попадания Z в область V ничтожно мала (46).
В этом случае говорят: расхождение гипотезы с данными опыта значительно.
Во втором случае гипотеза согласуется с данными опыта, т.к. при этой гипотезе вероятность попадания в область  равна
равна  .
.
Расхождение гипотезы с опытом незначимо.
Термины:
V – критическая область;
 - область принятия гипотезы;
- область принятия гипотезы;
a - уровень значимости;
 - критерий проверки гипотезы.
- критерий проверки гипотезы.
3. На практике критическую область V находят следующим образом. Вычисляют квантиль случайной величины  уровня
уровня 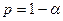 . Тогда V – множество значений Z, больших либо равных
. Тогда V – множество значений Z, больших либо равных  (рис. (33)).
(рис. (33)).
|
 V
V
 |

Рис.33
В самом деле, из определения квантиля следует:
 .
.
|
из
5.00
|
Обсуждение в статье: Доверительные интервалы для математического ожидания и дисперсии |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

