Закон больших чисел в форме Чебышева

На практике хорошо известна следующая закономер­ность, которую можно сформулировать так: среднее арифме­ти­ческое большого числа независимых однотипных случай­ных факторов практически неслучайно. Например, среднее арифме­тическое большого числа измерений одной и той же величины практически не отличается от истинного значения этой вели­чины; средняя кинетическая энергия большого числа хаотически движущихся молекул практически неслучайна и характеризует температуру тела.

Методы теории вероятностей позволяют дать строгую математическую формулировку этого закона.

Пусть имеется бесконечная последовательность слу­чай­ных величин

x₁, x₂, … , x_n, … (29)

Будем кратко называть случайные вели­чины (29) однотипными, если они имеют одно и тоже математическое ожидание а и одну и туже дисперсию D.

Теорема.Пусть случайные величины (29) однотипны и независимы, тогда имеет место соотношение

при n ® ¥, (30)

где а = М [x_k], k = 1, 2, …, e – любое как угодно малое положительное число.

Это означает: при достаточно большом n с практической достоверностью (с вероятностью » 100%) выполняется равенство

.

Эта теорема впервые была доказана русским математиком П.Л. Чебышевым. Доказательство теоремы основано на трех леммах.

 

Лемма 1. Пусть случайная величина h≥ 0. Тогда спра­ведливо неравенство

Р (h≥ D) ≤ 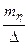, (31)

где D – любое положительное число.

Доказательство проведем для непре­рывной случайной величины. Плотность вероятности случайной величины h f (х) = 0 при х < 0, так как h≥ 0.

По определению математического ожидания имеем:

≥ ≥

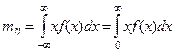(h≥ D),

откуда следует неравенство (31).

Лемма 2. Пусть x – случайная величина с числовыми характеристиками (а, D), тогда справедливо неравенство:

Р (| x – a| <e ) ≥ 1 – .

Доказательство. Имеем

Р (| x – a| ≥ e ) = P ((x – a)² ≥ e ²) ≤ .

Здесь использовано неравенство (31) при h = (x – a)², D = e ².

Из полученного неравенства следует

Р (| x – a| <e ) = 1 – Р (| x – a| ≥ e ) ≥ 1 – .

 

Лемма 3. Пусть x₁, x₂, …, x_n - независимые однотипные случайные величины с числовыми характеристиками (а, D). Тогда при любом e>0справедливо неравенство

≥ 1 – . (32)

где e – любое положительное число, a = M [x_i], D = D [x_i], i = 1, 2, …, n..

Неравенство (32) называется неравенством Чебышева.

Доказательство. Обозначим

.

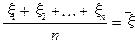Из свойств математиче­ского ожидания и дисперсии для независимых случайных величин следует:

Таким образом, случайная величина имеет числовые характеристики ; применяя к ней лемму 2, получим требуемое неравенство (32).

Доказательство теоремы Чебышева.

В силу неравенства Чебышева (32) имеем при любом n двойное неравенство

1 ≥ ≥ 1 – .

Переходя к пределу при n ® ¥ и учитывая теорему сравнения из теории пределов, получим требуемое соотношение (30).

Замечание. Введем удобный термин. Пусть имеется последовательность случайных величин

h₁, h₂, …, h_n, … . (33)

Говорят, что последовательность (33) сходится по вероятности к неслучайной величине а и пишут

при n ® ¥,

если для любого e > 0 выполняется соотношение

Р (| h_n – a| <e ) ® 1 при n ® ¥.

 

Очевидно, теорема Чебышева может быть сформулирована так: среднее арифметическое независимых однотипных случайных величин при неограниченном увеличении числа слагаемых сходится по вероятности к их общему математическому ожиданию.

Пример. Сколько надо провести независимых равноточных измерений данной величины, чтобы с вероятностью не менее 0,95 гарантировать отклонение среднего арифметического этих измерений от истинного значения величины не более, чем на 1 (по абсолютной величине), если СКО каждого измерения не превосходит 5?

Решение. Пусть x_i – результат i-го измерения (i = 1,2,…, n), a – истинное значение измеряемой величины, то есть M [x_i] = a при любом i; с учетом равноточности измерений x_i имеют одинаковую дисперсию D ≤ 25. В силу независимости измерений x_i – независимые случайные величины.

Необходимо найти n, при котором

≥ 0,95.

 

В соответствии с неравенством Чебышева (32) данное неравенство будет выпол­няться, если

1 – ≥ 1– 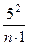≥ 0,95, откуда легко найти

n ≥500 измерений.

Теорема Бернулли

 

В начале курса теории вероятностей было сформулиро­вано: вероятность случайного события есть доля наступле­ния этого события в длинной серии независимых одинаковых испытаний. Укажем строгую математическую формулировку этого утверждения.

Пусть выполняется серия n независимых одинаковых испытаний и при каждом испытании событие А наступает с вероятностью р (схема Бернулли). Обозначим

Wn =	число наступлений события А	.
n

Число W_n называется частотой события А в серии из n испытаний.

Теорема. В указанной ситуации при неограниченном возрастании числа независимых испытаний частота случайного события А сходится по вероятности к вероятности этого события:

при n ® ¥.

Доказательство. Очевидно, W_n – случайная величина, при этом справедливо равенство

, где

x_i – число наступлений события А в i -ом испытании.

Проверим, что случайные величины x_i удовлетворяют условиям теоремы Чебышева.

1. x₁, x₂, … , x_n независимы в силу независимости испытаний.

2. Закон распределения случайной величины x_i для всех i = 1, …, n имеет вид

x_i = , q = 1 – p. (34)

Отсюда

M [x_i] = p · 1 + 0 · q = p,

D [x_i] = p (1 – p)² + q (0 – p)² = pq. (35)

Следовательно, случайные величины x_i однотипны с числовыми характеристиками: а = р, D = pq.

В силу теоремы Чебышева среднее арифметическое этих случайных величин сходится по вероятности к их общему математическому ожиданию:

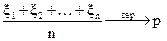при n ® ¥,

что и требовалось.

Замечание 1. Из сказанного выше следует: число успехов (наступлений события А в схеме Бернулли) дается формулой

x=x₁+ x₂+ … + x_n, (36)

где x_I – число успехов в i-ом испытании.

Из (35), (36) следует:

M [x] = n p, D [x] = npq. (37)

Таким образом, числовые характеристики биномиальной случайной величины с параметрами (n, p) даются формулами (37).

Замечание 2. Индикатором связанного с испытанием события А называется случайная величина, равная 1, если событие А произойдет и 0, если событие А не произойдет. Очевидно, закон распределения индикатора имеет вид (34), где р – вероятность наступления, q – вероятность ненаступления события А.