По теме практического занятия №5

1.Вычислить заданный интеграл непосредственным интегрированием удается далеко не всегда. В этих случаях одним из эффективных приемов является метод подстановки или замены переменной интегрирования. Сущность этого метода заключается в том, что путем введения новой переменной интегрирования удается свести заданный к новому интегралу, который сравнительно легко берется непосредственно. Этот метод описывается следующей формулой:

2.Если , - дифференцируемые функции от 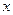, то из формулы для дифференциала произведения двух функций

получается формула интегрирования по частям

Задания для практического занятия №5

Вариант №1.

1. Найдите интегралы методом замены переменной (метод подстановки):

а) ; б) ; в) ; г) .

2. Найдите интегралы методом интегрирования по частям:

а) ; б) ; в) ; г) .

Вариант №2.

1. Найдите интегралы методом замены переменной (метод подстановки):

а) ; б) ; в) ; г) .

2. Найдите интегралы методом интегрирования по частям:

а) ; б) ; в) ; г) .

а) ; б) ; в) .

Вариант №3.

1. Найдите интегралы методом замены переменной (метод подстановки):

а) ; б) ; в) ; г) .

2. Найдите интегралы методом интегрирования по частям:

а) б) в) г)

Вариант №4.

1. Найдите интегралы методом замены переменной (метод подстановки):

а) ; б) ; в) ; г) .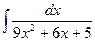

2. Найдите интегралы методом интегрирования по частям:

а) ; б) ; в) ; г) .

Инструкция по выполнению практического занятия №5:

1. Прочитайте краткие теоретические и учебно-методические материалы по теме практического занятия.

2. Устно ответьте на вопросы для закрепления теоретического материала к практическому занятию.

3. Выберите свой вариант (задания для практического занятия).

4. Внимательно прочитайте каждое задание. Определите, к какому виду относятся данные интегралы.

5. В первом задании интегралы находите методом подстановки. В заданиях под буквами а) и б) замените функции в скобках. В задании под буквой г) выделите в знаменателе полный квадрат и сделайте замену выражения в скобке, приведя данный интеграл к табличному.

6. Для выполнения второго задания нужно использовать метод интегрирования по частям. В задании под буквой а) за лучше взять тригонометрическую функцию, в задании б) – показательную функцию. В задании под буквой в) возьмите за логарифмическую функцию, а в задании г) – тригонометрическую. В некоторых заданиях после применения формулы интегрирования по частям необходимо применить метод подстановки.

7. Проверьте правильность решения заданий.

8. Убедившись, что задания решены правильно на черновике, аккуратно спишите их в чистовик.